Next: 演習問題詳解 Up: 積分公式 Previous: ガウスの発散定理 目次
Stokesの定理
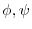 の共通な定義域内にある任意の曲面
の共通な定義域内にある任意の曲面 の境界線
の境界線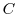 について次の式を証明せよ.
について次の式を証明せよ.
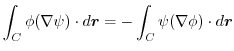
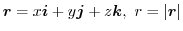 とし,
とし,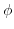 をスカラー場とする.任意の曲面
をスカラー場とする.任意の曲面 とその境界線
とその境界線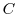 について次の式を証明せよ.
について次の式を証明せよ.
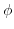 とベクトル場
とベクトル場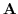 の共通な定義域内にある任意の曲面
の共通な定義域内にある任意の曲面 の境界線
の境界線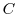 について次の式を証明せよ.
について次の式を証明せよ.
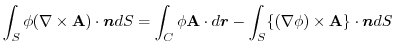
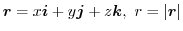 とし,
とし,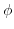 をスカラー場とする.任意の曲面
をスカラー場とする.任意の曲面 とその境界線
とその境界線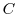 について次の式を証明せよ.
について次の式を証明せよ.
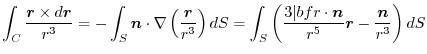
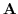 は全空間で定義されているとする.任意の曲面の境界線
は全空間で定義されているとする.任意の曲面の境界線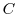 について
について
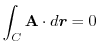
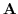 はスカラー・ポテンシャルをもつ.以上のことを証明せよ.
はスカラー・ポテンシャルをもつ.以上のことを証明せよ.