Next: ストークスの定理 Up: 積分公式 Previous: 積分公式 目次
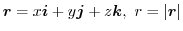 とする.任意の領域
とする.任意の領域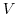 とその境界面
とその境界面 について次の等式を証明せよ.
について次の等式を証明せよ.
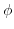 内の任意の領域
内の任意の領域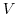 の境界面
の境界面 について次の等式を証明せよ.
について次の等式を証明せよ.
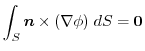
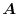 が
が
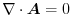 を満足しているとする.このベクトル場内にある曲面
を満足しているとする.このベクトル場内にある曲面 の境界線になっている閉曲線
の境界線になっている閉曲線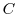 をとる.このとき,面積分
をとる.このとき,面積分
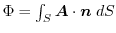 は
は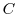 を境界線にもつどんな曲面
を境界線にもつどんな曲面 についても常に同一の値をもち,その値は閉曲線
についても常に同一の値をもち,その値は閉曲線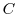 によって定まる.以上のことを証明せよ.この
によって定まる.以上のことを証明せよ.この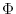 を閉曲線
を閉曲線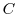 を貫く流速という.
を貫く流速という.
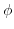 とベクトル場
とベクトル場
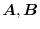 の共通の定義域内にある,任意の領域
の共通の定義域内にある,任意の領域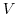 とその境界面
とその境界面 について次の等式を証明せよ.
について次の等式を証明せよ.
(4)
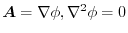 ならば,
ならば,
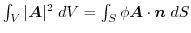
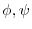 の共通の定義域内にある,任意の領域
の共通の定義域内にある,任意の領域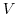 とその境界面
とその境界面 について次の等式を証明せよ.
について次の等式を証明せよ.
(3)
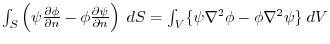 グリーンの公式
グリーンの公式
(4) 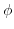 が調和関数であれば
が調和関数であれば
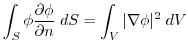
(5)
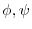 が調和関数であれば
が調和関数であれば
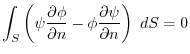
(6)  上で
上で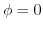 (または,
(または,
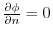 )ならば,調和関数
)ならば,調和関数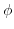 は
は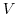 内で0 (または,定数)である.
内で0 (または,定数)である.
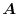 は全空間で定義されているとする.任意の領域の境界面
は全空間で定義されているとする.任意の領域の境界面 について
について
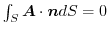 ならば,
ならば,
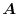 はベクトル・ポテンシャルをもつ.以上のことを証明せよ.
はベクトル・ポテンシャルをもつ.以上のことを証明せよ.
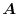 は全空間で定義されているとする.任意の領域の境界面
は全空間で定義されているとする.任意の領域の境界面 について
について
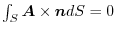 ならば,
ならば,
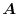 はスカラー・ポテンシャルをもつ.以上のことを証明せよ
はスカラー・ポテンシャルをもつ.以上のことを証明せよ