Next: 面積分(surface integrals) Up: スカラー場・ベクトル場 Previous: 勾配と方向微分係数 目次
 の中で質点が曲線
の中で質点が曲線
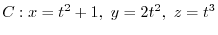
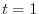 から
から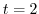 まで運動する間に力
まで運動する間に力
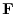 がする仕事量
がする仕事量
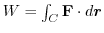 を求めよ.
を求めよ.
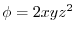 ,ベクトル場
,ベクトル場
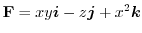 がある.媒介変数表示
がある.媒介変数表示
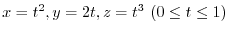 で表される曲線を
で表される曲線を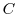 とする.次の線積分を求めよ.
とする.次の線積分を求めよ.
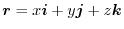 とする.任意の閉曲線
とする.任意の閉曲線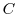 について
について
 であることを証明せよ.
であることを証明せよ.
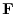 がポテンシャル
がポテンシャル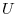 をもつとする.この力の場内で質量
をもつとする.この力の場内で質量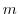 の質点が運動して,点Aから点Bまで移動したとき,次の式が成り立つことを証明せよ.
の質点が運動して,点Aから点Bまで移動したとき,次の式が成り立つことを証明せよ.
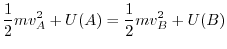
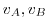 はそれぞれ点A,Bにおけるこの質点の速度ベクトルの大きさである.
はそれぞれ点A,Bにおけるこの質点の速度ベクトルの大きさである.
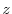 軸を除外した領域
軸を除外した領域 で
で
 は定義されている.
は定義されている.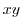 平面上で原点Oを中心とし,半径
平面上で原点Oを中心とし,半径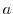 の円を
の円を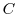 とする.次の等式を証明せよ.
とする.次の等式を証明せよ.