Next: 線積分 Up: スカラー場・ベクトル場 Previous: スカラー場・ベクトル場 目次
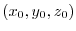 を通る勾配は,点
を通る勾配は,点
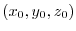 を通る等位面に直交することを示せ.
を通る等位面に直交することを示せ.
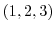 で曲面
で曲面
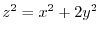 に直交する単位ベクトル(法線単位ベクトル) と
に直交する単位ベクトル(法線単位ベクトル) と 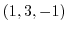 方向の方向微分係数と椄平面の方程式を求めよ.
方向の方向微分係数と椄平面の方程式を求めよ.
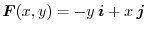 の流線を求めよ.
の流線を求めよ.
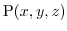 の位置ベクトルを
の位置ベクトルを
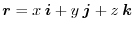 ,ベクトル場を
,ベクトル場を
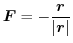 とすると,このベクトル場は原点を除くどの領域でも保存場であり
とすると,このベクトル場は原点を除くどの領域でも保存場であり
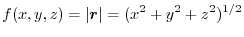
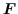 のスカラーポテンシャルであることを示せ.
のスカラーポテンシャルであることを示せ.
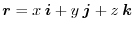 とスカラー場
とスカラー場
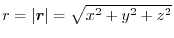 について,次の式を証明せよ.
について,次の式を証明せよ.
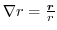
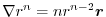
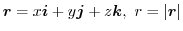 . Then find
. Then find
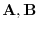 ..
..
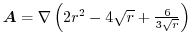
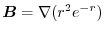
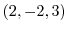 における
における
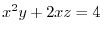 の法線単位ベクトル
の法線単位ベクトル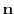 を求めよ .
を求めよ .
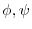 において
において
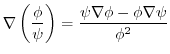
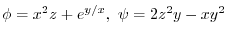 について,次のものを求めよ.
について,次のものを求めよ.
(2)
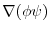 の点P
の点P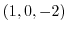 における値
における値
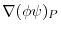
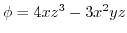 の点P
の点P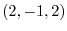 における,単位ベクトル
における,単位ベクトル
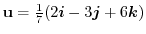 の方向への方向微分係数を求めよ.
の方向への方向微分係数を求めよ.
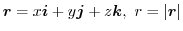 とする.次の
とする.次の
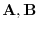 を求めよ.
を求めよ.
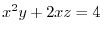 上の点P
上の点P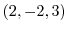 における法線単位ベクトル
における法線単位ベクトル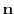 を求めよ.
を求めよ.
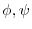 について次の式を証明せよ.
について次の式を証明せよ.
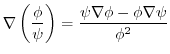
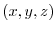 , Q
, Q
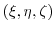 間の距離を
間の距離を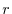 とする.微分演算子
とする.微分演算子