next up previous contents index
Next: 統計的推定法 Up: 確率分布 Previous: 確率分布   目次   索引

確率分布

例題 2..1  

サイコロを6回投げるとき，$ E =$ 「1の目がでる」という事象のおきる確率は $ P(E) = \frac{1}{6}$で与えられる．このとき，$ X = $「事象$ E$が発生する回数」とおくと，$ X$は0から6までの7個の値をとる変数で，

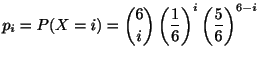
$\displaystyle p_{i} = P(X = i) = \binom{6}{i}\left(\frac{1}{6}\right)^{i}\left(\frac{5}{6}\right)^{6-i}$

で与えられます．したがって，$ X$は確率変数で，その確率分布は2項分布(binomial distribution)とよばれ， $ X \sim B(6,\frac{1}{6})$と表します．

次の1～3を満たす試行をベルヌーイ試行といいます．

  1. 各試行において，その事象が発生するか否かのみを問題にする
  2. 各試行は統計的に独立
  3. 対象とする事象が発生する確率は，各試行を通じて一定

1回の試行において，ある事象$ X$が発生する確率を$ p$とします．$ n$回のベルヌーイ試行列において，ちょうど$ i$回事象$ X$が発生する確率は

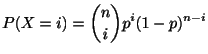
$\displaystyle P(X = i) = \binom{n}{i}p^{i}(1-p)^{n-i}$

で表され，このとき$ X$の確率分布を2項分布といい， $ X \sim B(n.p)$と表します．

確率変数$ X$のとる値が有限個または，無限個であっても自然数で番号が付けられる場合，確率変数$ X$は離散型であるという．また，確率変数$ X$がある区間内の全ての実数を取り得る場合，連続型であるという．

離散型の場合

確率変数$ X$のとる値を $ x_{1},x_{2},\ldots,x_{n}$とし，各事象 $ (X = x_{i})$の確率を $ p_{1},p_{2},\ldots,p_{n}$とするとき，

$\displaystyle P(X = x_{i}) = p_{i} (i = 1,2,\ldots, n) \sum{p_{i}} = 1, (p_{i} \geq 0)$

で表される．これより，$ X$の確率分布$ f$は

Xの値 $ x_{i}$ $ x_{1}$ $ x_{2}$ $ \cdots$ $ x_{n}$
$ P(X = x_{i}) = p_{i} = f(x_{i})$ $ p_{1}$ $ p_{2}$ $ \cdots$ $ p_{n}$
また，確率変数$ X$のとる値を $ x_{1} < x_{2} < \cdots < x_{n}$とするとき，その分布関数$ F(x_{r})$は次のように求められる．

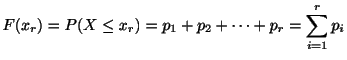
$\displaystyle F(x_{r}) = P(X \leq x_{r}) = p_{1} + p_{2} + \cdots + p_{r} = \sum_{i=1}^{r}p_{i}$

確率分布$ f$と分布関数$ F$は次の性質をもつ．

  1. $ 0 \leq p_{i} = f(x_{i}) \leq 1 (i = 1,2,\ldots, n)$
  2. $ F(x_{n}) = P(X \leq x_{n}) = p_{1} + p_{2} + \cdots + p_{n} = 1$
  3. $ P(a < X \leq b) = F(b) - F(a)$
  4. $ a < b$ $ \Longrightarrow$ $ F(a) < F(b)$

平均と分散

確率変数$ X$の平均(期待値)と分散は次の式で定義されます．

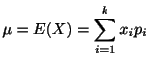
$\displaystyle \mu = E(X) = \sum_{i=1}^{k}x_{i}p_{i}$

$\displaystyle \sigma^2 = V(X) = E\left((X- \mu)^2\right) =E(X^2) - E(X)^2$

例題 2..2  

$ E(X) = \sum_{i=1}^{k}x_{i}p_{i}, E(Y) = \sum_{j=1}^{l}y_{j}q_{j}$のとき，

$\displaystyle E(X + Y ) = E(X) + E(Y)$

が成り立つことを示そう．

解答 $ P(X = x_{i}, Y = y_{j})$を$ p_{ij}$で表すと

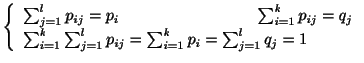
$\displaystyle \left\{\begin{array}{l} \sum_{j=1}^{l}p_{ij} = p_{i}\hskip 3cm \s... ...1}^{l}p_{ij} = \sum_{i=1}^{k}p_{i} = \sum_{j=1}^{l}q_{j} = 1 \end{array}\right.$

これより，
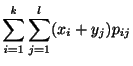$\displaystyle E(X + Y)$ $\displaystyle =$ $\displaystyle \sum_{i=1}^{k}\sum_{j=1}^{l}(x_{i} + y_{j})p_{ij}$  
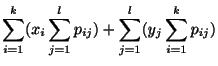  $\displaystyle =$ $\displaystyle \sum_{i=1}^{k}(x_{i}\sum_{j=1}^{l}p_{ij}) + \sum_{j=1}^{l}(y_{j}\sum_{i=1}^{k}p_{ij})$  
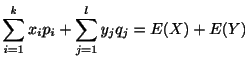  $\displaystyle =$ $\displaystyle \sum_{i=1}^{k}x_{i}p_{i} + \sum_{j=1}^{l}y_{j}q_{j} = E(X) + E(Y)$  

例題 2..3  

$ E((X - \mu)^2) = E(X^2) - (E(X))^2$が成り立つことを示そう．

解答

$\displaystyle E((X - \mu)^2)$ $\displaystyle =$ $\displaystyle E(X^2 - 2X\mu + \mu^2)$  
  $\displaystyle =$ $\displaystyle E(X^2) - 2\mu E(X) + \mu^2 E(1)$  
  $\displaystyle =$ $\displaystyle E(X 2) - 2E(X)E(X) + E(X)^2 = E(X^2) - E(X)^2$  

連続型の場合 確率密度関数

連続変量の確率分布において，任意の定数 $ a,b (a < b)$に対して，確率
$ P_{r}(a \leq X \leq b)$が

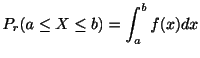
$\displaystyle P_{r}(a \leq X \leq b) = \int_{a}^{b} f(x) dx $

で与えられるような連続関数$ f(x)$が $ (-\infty,\infty)$で存在するとき，この$ f(x)$を，この確率分布の確率密度関数(probability density function)といいます．また，確率密度関数は次の性質を持っています．

$\displaystyle f(x) \geq 0 $

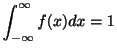
$\displaystyle \int_{-\infty}^{\infty} f(x) dx = 1 $

確率分布

確率変数$ X$が区間 $ -\infty < X \leq x$にある確率が

$\displaystyle F(x) = P_{r}(X \leq x) $

で定められる関数$ F(x)$を，確率変数$ X$の確率分布(probability distribution)といいます．

平均と分散

確率変数$ X$の平均(期待値)と分散は次の式で定義されます．

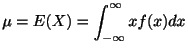
$\displaystyle \mu = E(X) = \int_{-\infty}^{\infty}x f(x) dx $

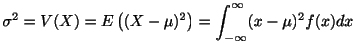
$\displaystyle \sigma^2 = V(X) = E\left((X- \mu)^2\right) = \int_{-\infty}^{\infty}(x - \mu)^2 f(x) dx $

正規分布

確率変数$ X$の確率密度関数が

$\displaystyle g(x) = \frac{1}{\sqrt{2\pi} \sigma} EXP\left[-\frac{(x-\mu)^2}{2 \sigma^2}\right], -\infty < x < \infty $

で与えられるとき，確率変数$ X$は正規分布に従うといい， $ X \sim N(\mu, \sigma^2)$と表わします．

$ X \sim N(3, 2^{2})$を表すと，次のようになります．

\includegraphics[width=14.5cm]{STATFIG/Fig2-1-1.eps}

このままでは，比較しにくいので，標準化(normalization)を行ないます．

標準化

確率変数$ X$の平均$ E(X)$を0に，分散$ V(X)$を1に直すことを標準化といいます．

標準化の方法

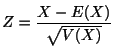
$\displaystyle Z = \frac{X - E(X)}{\sqrt{V(X)}} $

とおくと

$\displaystyle E(Z) = 0, V(Z) = 1 $

になります．

$ P_{r}(Z \leq z)$を求めるには， $ P_{r}(Z \leq z) = P_{r}(Z \leq 0) + P_{r}(0 < Z \leq z)$を求めます． $ P_{r}(Z \leq 0)$は標準正規分布の左半分なので，その値は0.5となります． $ P_{r}(0 < Z \leq z)$の値は標準正規分布表を用いて求めます．

図: 正規分布
\begin{figure}\begin{center} \includegraphics[width=6cm]{STATFIG/Fig4-1.eps} \end{center}\end{figure}

例題 2..4  

$ X \sim N(60.9, 2.9^2)$のとき，
(1) $ P(X \leq 63.8)$を求めよ
(2) $ P(62.3 < X \leq 63.0)$を求めよ．

解答
(1) 標準化を行うと，

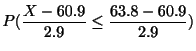$\displaystyle P(X \leq 63.8)$ $\displaystyle =$ $\displaystyle P(\frac{X - 60.9}{2.9} \leq \frac{63.8 - 60.9}{2.9})$  
  $\displaystyle =$ $\displaystyle P(Z \leq \frac{2.9}{2.9}) = P(Z \leq 1)$  
  $\displaystyle =$ $\displaystyle P(Z \leq 0) + P(0 \leq Z \leq 1) = 0.5 + 0.3413 = 0.8413$  

(2)

    $\displaystyle P(\frac{62.3-60.9}{2.9} < \frac{X - 60.9}{2.9} \leq \frac{63.0 - 60.9}{2.9})$  
  $\displaystyle =$ $\displaystyle P(\frac{1.4}{2.9} < Z \leq \frac{2.1}{2.9}$  
  $\displaystyle =$ $\displaystyle P(0.48 < Z \leq 0.72)$  
  $\displaystyle =$ $\displaystyle P(0 \leq Z \leq 0.72) - P(0 \leq Z \leq 0.48)$  
  $\displaystyle =$ $\displaystyle 0.2642 - 0.1844 = 0.0798$  

統計学演習問題 4

1. $ X \sim N(80,6^2)$のとき，次の確率を求めよ．

(a) $ P_{r}(X \leq 90)$

(b) $ P_{r}(\vert X - 80\vert \leq 12)$

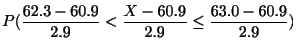2. 都市Aの夏期を除く各期の一人一日当たりの水需要量は，これまでの何年かの実績からほぼ $ N(210,21^2)$に従うことが分かっているとする．今年の一人当たりの水需要量(夏期を除く)が250(l/人)以上になる確率を求めよ．

next up previous contents index
Next: 統計的推定法 Up: 確率分布 Previous: 確率分布   目次   索引