Next: 確率変数の平均値と分散(Expectation and Variance) Up: 確率変数 Previous: 確率変数(Random variable) 目次
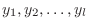
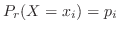
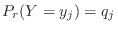
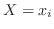 かつ
かつ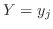 」という事象の確率を
」という事象の確率を
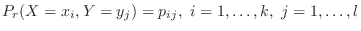
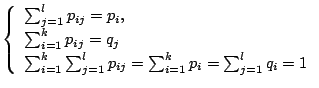
1. 2個のサイコロの出る目の確率変数を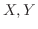 とするとき,積
とするとき,積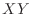 の確率分布と分布関数を求めよ.
の確率分布と分布関数を求めよ.
2. 一枚の銅貨を投げて表が出れば1,裏が出れば0と表すことにする.3枚の銅貨を投げるとき,それぞれの銅貨の表が出ることの確率変数を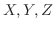 とする.
とする.
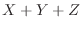 の確率分布を求めよ.
の確率分布を求めよ.
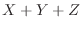 の分布関数を求めよ.
の分布関数を求めよ.