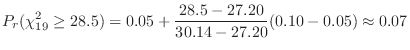Next: この文書について... Up: 確率論入門 Previous: F分布(F distribution) 目次
1
(a) ここでは
 の
の の中に異なる数字を入れて4桁の数字を何個作れるか考えてみます.まず,4桁の数字なので,千の位の
の中に異なる数字を入れて4桁の数字を何個作れるか考えてみます.まず,4桁の数字なので,千の位の には0を使うことができません.そこで千の位は1から6までの6個の中から1個選ぶことになるので,6通り.百の位から一の位までは0から6までのどの数字も使うことができます.しかし,数字を取り出して並べるため,同じ数字は2度使えないことに注意して下さい.では並べてみましょう.
には0を使うことができません.そこで千の位は1から6までの6個の中から1個選ぶことになるので,6通り.百の位から一の位までは0から6までのどの数字も使うことができます.しかし,数字を取り出して並べるため,同じ数字は2度使えないことに注意して下さい.では並べてみましょう.
まず,百の位には千の位で用いられた数字以外どれでも使えるので,6通りあります.十の位は千の位と百の位で用いられた数字以外どれでも使えるので,5通りあります.最後に一の位は千の位,百の位,十の位で用いられたもの以外すべて使えるので4通り.よって全部で
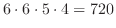
ここで百の位,十の位,一の位は千の位で用いられた数字以外どれでも1回づつ使うことができることに注意すると,6個の中から3個を取り出し順序をつけて並べる順列の数になるので
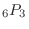 と表わせます.よって
と表わせます.よって
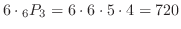
(b) まず,5の倍数は一の位が必ず,0か5になることに注意します.次に,一の位が0の場合と5の場合を別々に考えます.
一の位が0の場合.
千の位,百の位,十の位は1から6までの数字を1回づつ使うことができるので,6個の中から3個を取り出し並べる順列の数になるので
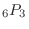 と表わせます.よって 120通り
と表わせます.よって 120通り
一の位が5の場合.
千の位に0が使えないので,千の位は0,5以外の5通り,百と十の位は一と千の位で用いた数字以外どれでも1回づつ使えるので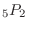 通り.よって
通り.よって
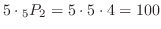 通り
通り
ここで,一の位が0の場合と5の場合は同時におきないので,全部で
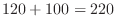 通り
通り
(c) 同じ数字が重複してもよいので,千の位は1から6までの6通り,百の位は0から6までの7通り,十の位も0から6までの7通り,最後に一の位も0から6までの7通り.したがって,
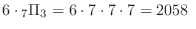 通り
通り
2
(a) 1から10までの番号のついたカードから6枚を取り出すとき,何通りの取り出し方があるかを考えます.このとき,一枚づつ順に取り出し並べるわけではないので,取り出す順序を考える必要はありません.よって,何通りの組み合わせがあるかを考えればよいでしょう.
10個の中から6個を取り出す組み合わせは
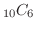 なので,
なので,
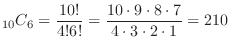 通り
通り
(b) 1と2のカードを含むとは取り出した6枚の中に必ず1と2のカードが入っていなければならないということです.
これは1と2を先に引いておいて残りの4枚を3から10までの8枚から選ぶ選び方と考えることができます.よって
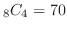 通り.
通り.
(c) 1のカードを含む場合を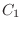 ,2のカードを含む場合を
,2のカードを含む場合を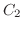 とします.すると
とします.すると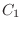 は
は
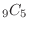 通り,
通り,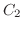 も
も
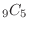 通りとなるので,1または2を含む場合は
通りとなるので,1または2を含む場合は
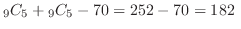 通り
通り
別解 1または2のカードを含むの否定は1と2のカードを含まないとなるので,1と2のカードを含まない場合を考えます.
1と2を含まないので残りの8枚のカードから6枚を取り出すことになるので,その取り出し方は
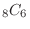 通り.よって,1または2のカードを含む場合は
通り.よって,1または2のカードを含む場合は
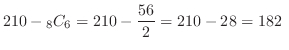 通り
通り
3
(a)
![$A_{i} = [表の出る回数がi回]$](img246.png) とおきます.すると表は5回中
とおきます.すると表は5回中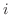 回どこで出てもよく出る順序は関係ないので,その組み合わせは
回どこで出てもよく出る順序は関係ないので,その組み合わせは
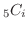 となります.
となります.
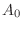 は
は
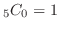 通り,
通り,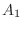 は
は
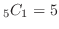 通り,
通り,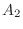 は
は
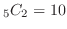 通り,
通り,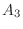 は
は
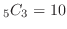 通り,
通り, 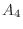 は
は
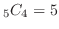 通り,
通り,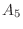 は
は
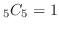 通り
通り
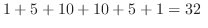 通り
通り
4
(a) 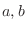 が隣り合うので,
が隣り合うので,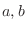 の順に並んでいるのを
の順に並んでいるのを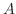 とおくと,この問題は5文字を一列に並べる並べ方は何通りあるかという問題と同じになります.したがって,
とおくと,この問題は5文字を一列に並べる並べ方は何通りあるかという問題と同じになります.したがって,
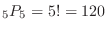
 の順に並んでいるのを
の順に並んでいるのを とおくと,
とおくと,
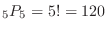
(b) 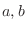 が隣り合わないのはすべての並び方から
が隣り合わないのはすべての並び方から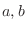 が隣り合う場合を引いたもの.よって
が隣り合う場合を引いたもの.よって
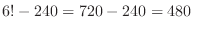 通り
通り
(c) 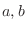 が両端にくるのは
が両端にくるのは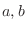 と
と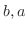 の場合があることに注意すると,中の4文字の並び方は
の場合があることに注意すると,中の4文字の並び方は
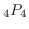 通りとなるので,全部で
通りとなるので,全部で
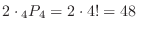 通り
通り
5
![]() . 全てに番号をつけて並べると,
. 全てに番号をつけて並べると,
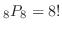 通りの並べかたがある.しかし,実際は4個の
通りの並べかたがある.しかし,実際は4個の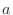 の重複
の重複
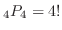 ,2個の
,2個の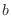 の重複
の重複
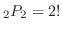 は区別できないので,その組み合わせは
は区別できないので,その組み合わせは
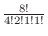 である.
である.
演習問題2.1
(a) まず,場合の数を使って確率を求めてみましょう.
![$X_{i} = [6回中i回1の目がでる]$](img273.png) とおきます.
とおきます.
さいころを6回投げると,目のでかたは全部で
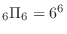 通りあります.次に1の目が6回中1回出る場合の数は何通りあるか数えてみましょう.
通りあります.次に1の目が6回中1回出る場合の数は何通りあるか数えてみましょう.
一投目で1の目が出ると,残りの5回は1以外なので,
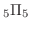 通り.同じことが二投目,三投目,... でも言えるので,全部で
通り.同じことが二投目,三投目,... でも言えるので,全部で
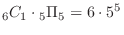
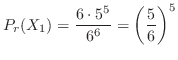
別解
まず,1の目が1回出るのは最初の1投目でも2投目でも6投目でもいいので全部で6通りあることに注意します.この6通りのそれぞれの確率を調べてみましょう.まず,1投目で1の目が出たとすると

 の中には1の目以外なんでも入ります.よってこのときの確率を求めると,
の中には1の目以外なんでも入ります.よってこのときの確率を求めると,
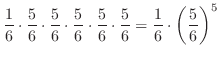
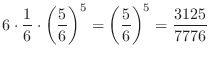
(b) 1の目が4回出る組み合わせは全部で
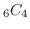 通り.そのとき,残りの2回は1以外なので
通り.そのとき,残りの2回は1以外なので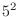 通り.よって全部で,
通り.よって全部で,
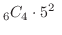 通り
通り
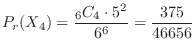
別解
6回中4回1の目がでる組み合わせは
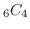 通り.また,それぞれの確率は
通り.また,それぞれの確率は
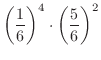
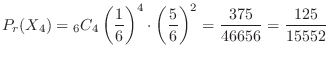
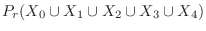 |
 |
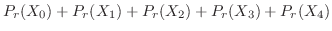 |
|
 |
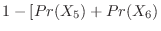 |
||
 |
![$\displaystyle 1 - \left[\binom{6}{5} \cdot \left(\frac{1}{6}\right)^5 \left(\frac{5}{6}\right) + \binom{6}{6} \cdot \left(\frac{1}{6}\right)^6 \right]$](img291.png) |
||
 |
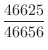 |
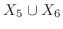
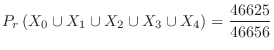
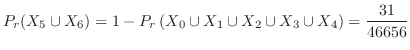
2.
(a) 白玉5個,赤玉3個,黒玉が2個合わせて10個の中から4個を取り出す組み合わせは
![]() 通り.次に白玉4個を袋の中から取り出す組み合わせを考えてみましょう.
通り.次に白玉4個を袋の中から取り出す組み合わせを考えてみましょう.
袋の中の5個の白玉から4個を取り出すしかないので,その組み合わせは
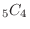 通り.したがって,取り出した4個が全て白玉の確率は
通り.したがって,取り出した4個が全て白玉の確率は
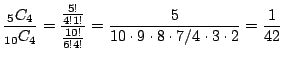
別解 取り出した4個に注目.
1. 白玉4個取り出す組み合わせは
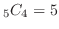 通り
通り
2. 白玉1個ずつ取り出す確率は,
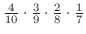
したがって,取り出した4個が全て白玉の確率は
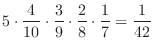
(b) 白玉5個,赤玉3個,黒玉が2個合わせて10個の中から4個を取り出す組み合わせは
![]() 通り.次に白玉2個を袋の中から取り出す組み合わせを考えてみましょう.
通り.次に白玉2個を袋の中から取り出す組み合わせを考えてみましょう.
2個だけ白玉ということは5個の白玉から2個取り出し,残りの赤玉と黒玉から2個取り出す場合の数なので,
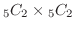 .したがって,取り出した4個のうち白がちょうど2個である確率は
.したがって,取り出した4個のうち白がちょうど2個である確率は
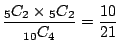
(c) 白が2個以内とは白が0個,1個,2個の事象の場合である.よって,その確率は
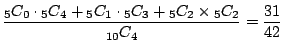
(d) 白が2個赤が2個を取り出す組み合わせは,
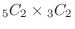 である.したがって,取り出した4個のうち白が2個赤が2個である確率は
である.したがって,取り出した4個のうち白が2個赤が2個である確率は
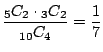
1. 白,赤,黒がともに含まれるということは,白,赤,黒のどれかが2個になる組み合わせを考えればよい.よって
![]() 通り.
通り.
2. 白,赤,黒1つずつ取り出す確率は
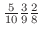 .
.
3.したがって,白,赤,黒がともに含まれる確率は
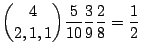
演習問題2.2
(a) 1から10までがその順に一列に並ぶ場合を考えているので,まずは,1から10を勝手に一列に並べる並べ方は何通りあるか考えてみましょう.
先頭にくるのは1から10の内どれでもよいので,10通り,次は9通り,...となるので,全部で
![]() 通りとなります.
通りとなります.
次に1から10までがその順に一列に並ぶ場合は一通り.したがって,その確率は
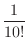
別解 1が先頭にくる確率は
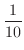 ,1が先頭にきたことが分ったあと,2が2番目にくる確率は
,1が先頭にきたことが分ったあと,2が2番目にくる確率は
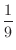 ,1が先頭,2が2番目にきたことが分ったあと,3が3番目にくる確率は
,1が先頭,2が2番目にきたことが分ったあと,3が3番目にくる確率は
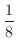 ,...となるので,1から10までがその順に一列に並ぶ確率は
,...となるので,1から10までがその順に一列に並ぶ確率は
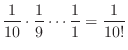
(b) 4のカードがちょうど4番目ということは,それ以外の9枚のカードはどこにあってもいいので,4のカードがちょうど4番目にくるのは
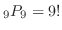 通りあります.よってその確率は
通りあります.よってその確率は
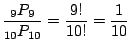
別解 4のカードがちょうど4番目にくる確率は
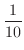
(c) 1が最初に,4が4番目にあるということは,それ以外の8枚のカードはどこにあってもいいので,全部で
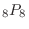 通り.よって,1が最初に,4が4番目にくる確率は
通り.よって,1が最初に,4が4番目にくる確率は
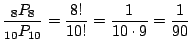
別解 1が最初にくる確率は
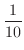 .次に1が最初にきたことが分ったあと,4が4番目にくる確率は
.次に1が最初にきたことが分ったあと,4が4番目にくる確率は
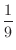 .よって,1が最初に,4が4番目にくる確率は
.よって,1が最初に,4が4番目にくる確率は
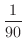
4. (a) 円板の半径は1.5cmよりちょうど正方形の中に入るには,円板の中心が1辺5cmの正方形の中にあればよい.したがって,その確率は
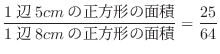
(b) A = 「円板が正方形の辺にかかる」の余事象は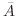 = 「円板が正方形の中にある」となる.したがって,その確率は
= 「円板が正方形の中にある」となる.したがって,その確率は

(c) 円板が4つの正方形にまたがるには,その中心が4つの正方形の境界から1.5cm以内になければならない.また,その面積は
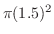 .したがって,円板が4つの正方形にまたがる確率は
.したがって,円板が4つの正方形にまたがる確率は
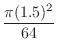
5.
(a) 白玉4個,赤玉6個,合わせて10個の中から2個を取り出す組み合わせは
![]() 通り.白玉2個を袋の中から取り出す組み合わせを考えてみましょう.
通り.白玉2個を袋の中から取り出す組み合わせを考えてみましょう.
袋の中の4個の白玉から2個を取り出すしかないので,その組み合わせは
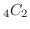 通り.したがって,取り出した2個が両方白玉の確率は
通り.したがって,取り出した2個が両方白玉の確率は
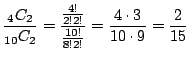
(b) 1個だけ白玉ということは4個の白玉から1個取り出し,6個の赤玉から1個取り出す場合の数なので,
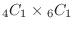 .よってその確率は
.よってその確率は
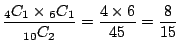
(c) 少なくとも1個は白玉という事象は,2個とも白玉であるか,または1個だけ白玉であるかのどちらかです.ここで,これらの事象は排反事象(同時に起きない)であることに注意すると,全部で,
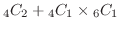 通り.したがって,求める確率は
通り.したがって,求める確率は
3. 1.
(a) 4回投げて少なくとも1回6の目がでるという事象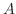 の余事象
の余事象
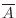 は,4回投げて一度も6の目がでないとなります.ここで,それぞれの回に6の目がでない確率は
は,4回投げて一度も6の目がでないとなります.ここで,それぞれの回に6の目がでない確率は
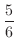 に注意すると,
に注意すると,
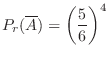
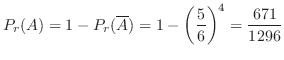
(b) 2個のさいころを同時に24回投げて少なくとも1回2個とも6の目がでるという事象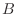 を考えます.まず,2個のさいころを同時に投げたとき,2個とも6の目がでる確率は
を考えます.まず,2個のさいころを同時に投げたとき,2個とも6の目がでる確率は
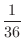 .
.
ここで,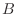 の余事象
の余事象
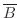 は,2個のさいころを同時に24回投げて一度も2個両方は6の目ではないとなります.
したがって,
は,2個のさいころを同時に24回投げて一度も2個両方は6の目ではないとなります.
したがって,
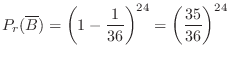
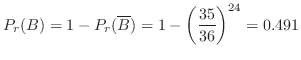
2 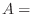 「真のガン患者」,
「真のガン患者」,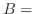 「精密検査で陽性反応がでた患者」とおくと質問は,患者がその精密検査の結果陽性反応を示した場合にガン患者である確率を求めることです.これは条件付き確率を用いると次のように表わせます.
「精密検査で陽性反応がでた患者」とおくと質問は,患者がその精密検査の結果陽性反応を示した場合にガン患者である確率を求めることです.これは条件付き確率を用いると次のように表わせます.
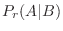
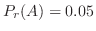 ,
,
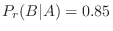 ,
,
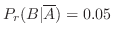 が分っていることに注意します.
ここで,Bayesの定理を用いると
が分っていることに注意します.
ここで,Bayesの定理を用いると
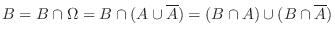
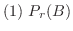 |
 |
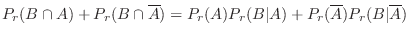 |
|
 |
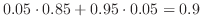 |
||
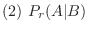 |
 |
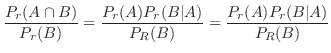 |
|
 |
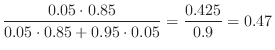 |
別解
3.
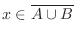 |
 |
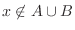 |
|
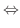 |
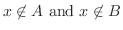 |
||
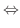 |
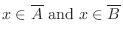 |
||
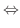 |
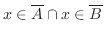 |
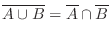
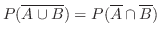
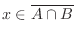 |
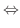 |
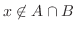 |
|
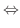 |
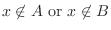 |
||
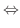 |
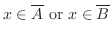 |
||
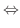 |
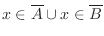 |
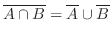
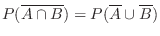
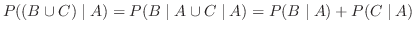
演習問題3.1
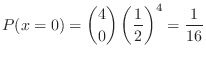
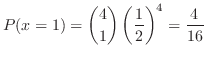
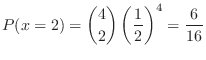
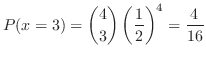
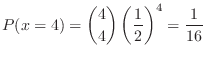
 は
は
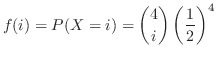
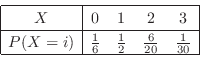
2. 10個から3個取り出す組み合わせは
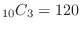 通り.また,3個中赤がゼロということは,白が3個と同じことなので,6個の白から3個取り出すこととなり,その組み合わせは
通り.また,3個中赤がゼロということは,白が3個と同じことなので,6個の白から3個取り出すこととなり,その組み合わせは
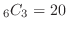 通り.よって,
通り.よって, を赤玉の個数とおくと,
を赤玉の個数とおくと,
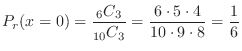
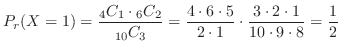
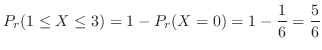
3.
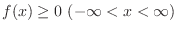
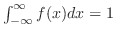
を満たしていることを示せばよい. そこで,
1. 定数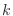 を0以上とすれば
を0以上とすれば
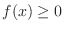 は満たされる.
は満たされる.
2.
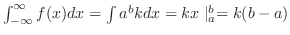 より
より
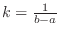 と定めればよい.
と定めればよい.
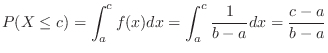
(4)
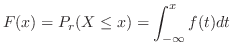
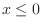 のとき
のとき
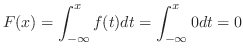
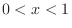 のとき
のとき
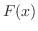 |
 |
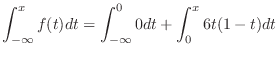 |
|
 |
![$\displaystyle 0 + \left[3t^2 - 2t^3\right]_{0}^{x} = 3x^2 - 2x^3$](img383.png) |
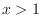 のとき
のとき
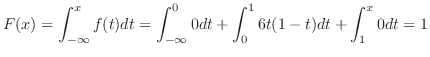
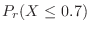 |
 |
![$\displaystyle P_{r}(0 < X \leq 0.7) = F(0.7) - F(0) = \left[F(x)\right]_{0}^{0.7}$](img387.png) |
|
 |
![$\displaystyle \left[3x^2 - 2x^3\right]_{0}^{0.7} = 3(0.7)^2 - 2(0.7)^3$](img388.png) |
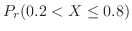 |
 |
![$\displaystyle \left[F(x)\right]_{0.2}^{0.8} = \left[3x^2 - 2x^3\right]_{0.2}^{0.8}$](img390.png) |
|
 |
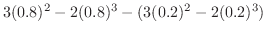 |
4.
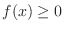 と
と
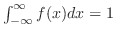 を示せばよいでしょう.
を示せばよいでしょう.
1.
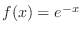 は指数関数より全ての
は指数関数より全ての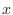 で
で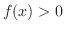 .
.
2.
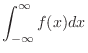 |
 |
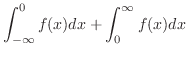 |
|
 |
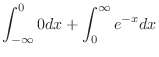 |
||
 |
![$\displaystyle \left[0 + -e^{-x} \right]_{0}^{\infty -} = 1$](img397.png) |
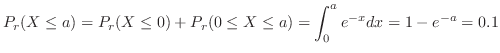
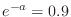 .したがって,
.したがって,
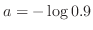
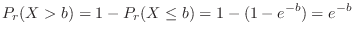
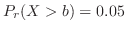 を満たす
を満たす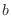 は
は
演習問題3.2
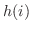 は
は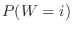 で与えれることに注意する.
まず,
で与えれることに注意する.
まず,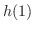 を考えてみよう.
を考えてみよう.
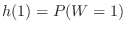 より,2個のサイコロを投げて両方1の目が出る確率を求めることと同じである.場合の数を求めると,両方1の目の組み合わせは36通り中の1通り.したがって
より,2個のサイコロを投げて両方1の目が出る確率を求めることと同じである.場合の数を求めると,両方1の目の組み合わせは36通り中の1通り.したがって
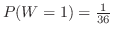 .同様に,
.同様に,
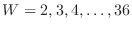 について求めると
について求めると

(2)
(a)
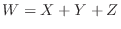 とおくと
とおくと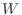 の変域は
の変域は
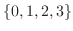 である.確率分布
である.確率分布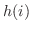 は
は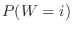 で与えられる.
まず,
で与えられる.
まず,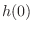 を考えてみよう.
を考えてみよう.
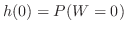 より,3枚銅貨を投げて全て裏が出る確率を求めることと同じである.場合の数を求めると,全部裏の組み合わせは8通り中の1通り.したがって
より,3枚銅貨を投げて全て裏が出る確率を求めることと同じである.場合の数を求めると,全部裏の組み合わせは8通り中の1通り.したがって
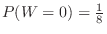 .同様に,
.同様に,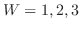 について求めると
について求めると
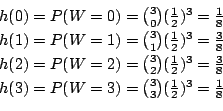
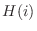 を求める.
を求める.
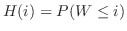 のことなので,
のことなので,
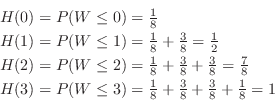
演習問題3.3
(1)
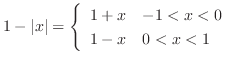
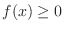 .また
.また
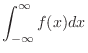 |
 |
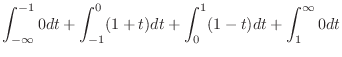 |
|
 |
![$\displaystyle \left[t + \frac{t^2}{2}\right]_{-1}^{0} + \left[t - \frac{t^2}{2}\right]_{0}^{1}$](img426.png) |
||
 |
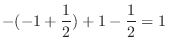 |
別解
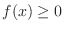 より,
より,
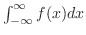 は
は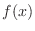 と
と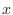 軸の間の面積と考えられる.したがって,求める面積は底辺2高さ1の三角形の面積より1.
軸の間の面積と考えられる.したがって,求める面積は底辺2高さ1の三角形の面積より1.
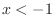 のとき
のとき
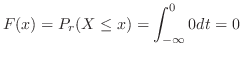
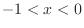 のとき
のとき
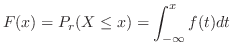 |
 |
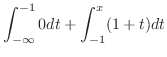 |
|
 |
![$\displaystyle \left[t + \frac{t^2}{2}\right]_{-1}^{x}$](img433.png) |
||
 |
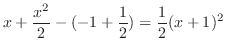 |
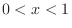 のとき,
のとき,
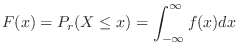 |
 |
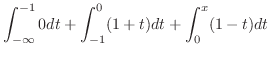 |
|
 |
![$\displaystyle \left[t + \frac{t^2}{2}\right]_{-1}^{0} + \left[t - \frac{t^2}{2}\right]_{0}^{x}$](img437.png) |
||
 |
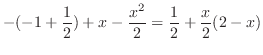 |
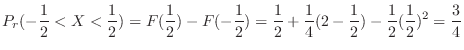
 |
 |
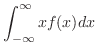 |
|
 |
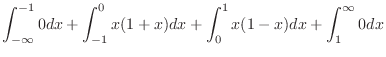 |
||
 |
![$\displaystyle \left[\frac{x^2}{2} + \frac{x^3}{3}\right]_{-1}^{0} + \left[\frac{x^2}{2} - \frac{x^3}{3}\right]_{0}^{1} = 0$](img442.png) |
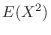 |
 |
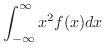 |
|
 |
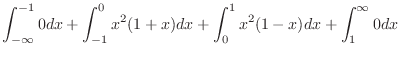 |
||
 |
![$\displaystyle \left[\frac{x^3}{3} + \frac{x^4}{4}\right]_{-1}^{0} + \left[\frac{x^3}{3} - \frac{x^4}{4}\right]_{0}^{1}$](img446.png) |
||
 |
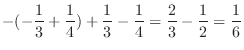 |
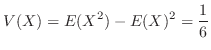
2.
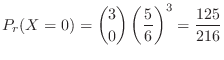
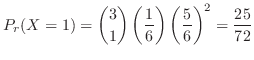
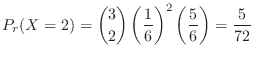
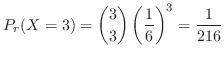
別解 この試行はベルヌーイ試行である.つまり,
ベルヌーイ試行を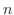 回行なったとき,事象の発生回数
回行なったとき,事象の発生回数 を
を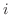 ,事象の発生確率を
,事象の発生確率を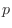 とすると
とすると
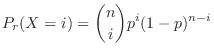
 は2項分布に従うといい,
は2項分布に従うといい,
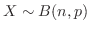 と表わします.このとき,
と表わします.このとき,
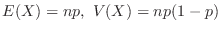
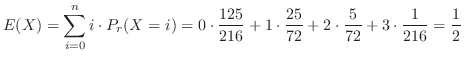
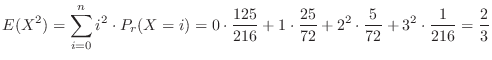
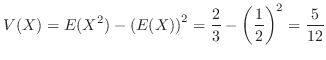
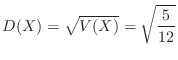
別解
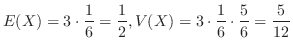
(c)  の標準化とは平均
の標準化とは平均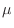 を0に分散
を0に分散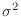 を1に変えることである.そこで
を1に変えることである.そこで の標準化は
の標準化は
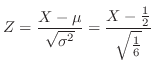
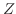 の確率分布を求めてみよう.
の確率分布を求めてみよう.

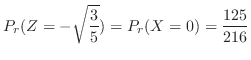
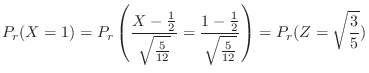
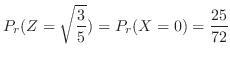
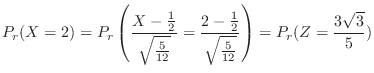
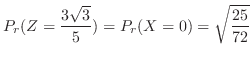
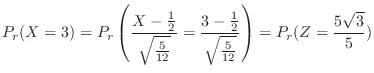
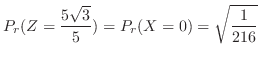
3
(a) Bernoulliの定理は試行回数が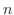 ,事象発生回数が
,事象発生回数が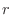 ,事象発生確率が
,事象発生確率が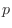 のとき
のとき
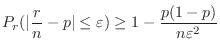
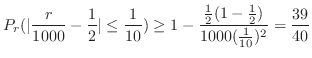
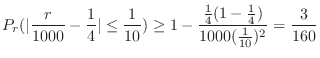
(c) この問題は試行回数が2000のとき,事象発生回数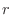 の偏りが50回以内である確率を求めよということである.言い換えると,2000回中の表が現われる割合
の偏りが50回以内である確率を求めよということである.言い換えると,2000回中の表が現われる割合
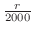 と理論的確率
と理論的確率
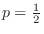 との誤差が
との誤差が
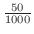 である確率を求めよということになる.そこでBernoulliの定理を用いると
である確率を求めよということになる.そこでBernoulliの定理を用いると
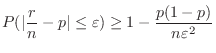
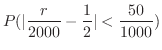 |
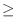 |
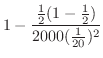 |
|
 |
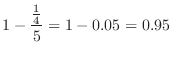 |
(d) この問題はn回中の表が現われる割合
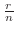 と理論的確率
と理論的確率
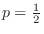 との誤差が
との誤差が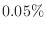 である確率が
である確率が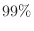 以上になるには何回以上投げればよいかということを聞いている.そこでBernoulliの定理を用いると
以上になるには何回以上投げればよいかということを聞いている.そこでBernoulliの定理を用いると
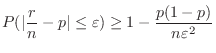
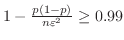 である
である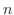 を求めればよい.
を求めればよい.
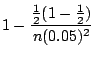 |
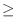 |
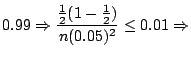 |
|
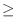 |
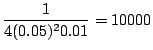 |
演習問題3.4
1.
(a)
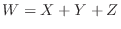 とおくと
とおくと の変域は
の変域は
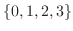 である.確率分布
である.確率分布 は
は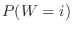 で与えれれる.
まず,
で与えれれる.
まず,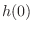 を考えてみよう.
を考えてみよう.
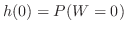 より,3枚銅貨を投げて全て裏が出る確率を求めることと同じである.場合の数を求めると,全部裏の組み合わせは8通り中の1通り.したがって
より,3枚銅貨を投げて全て裏が出る確率を求めることと同じである.場合の数を求めると,全部裏の組み合わせは8通り中の1通り.したがって
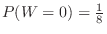 .同様に,
.同様に,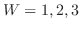 について求めると
について求めると
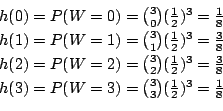
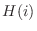 を求める.
を求める.
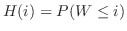 のことなので,
のことなので,
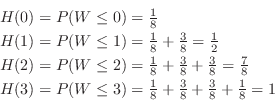
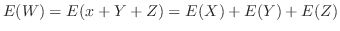
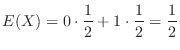
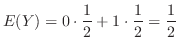
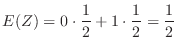
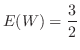
別解 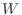 の確率分布が分かっているので,直接求めることも可能である.
の確率分布が分かっているので,直接求めることも可能である.
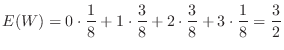
次に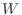 の分散
の分散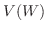 を求める.一般に
を求める.一般に
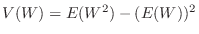 を用いて求める方が簡単であるが,この問題では
を用いて求める方が簡単であるが,この問題では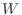 の確率分布が分かっているので直接求める方が簡単である.
の確率分布が分かっているので直接求める方が簡単である.
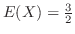 より
より
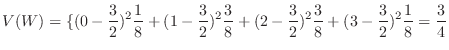
2.
(a) 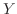 の確率密度関数
の確率密度関数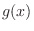 を求めるには
を求めるには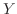 の分布関数
の分布関数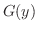 について調べ,
について調べ,
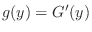 の関係を用いる.
の関係を用いる.
 の分布関数
の分布関数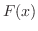 は
は
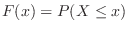 ,
,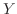 の分布関数
の分布関数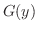 は
は
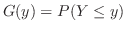 で与えられるので,
で与えられるので,
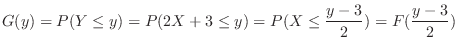
 の確率密度関数は
の確率密度関数は
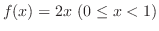 で与えられていることに注意すると,
で与えられていることに注意すると, の確率密度関数
の確率密度関数 は,
は,
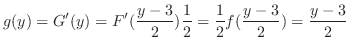
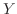 の期待値
の期待値
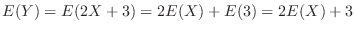 より
より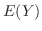 を求めるには,
を求めるには,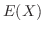 を求めればよいことが分かる.
を求めればよいことが分かる.
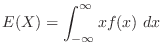 で与えられるので,
で与えられるので,
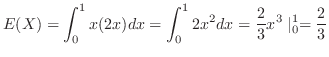
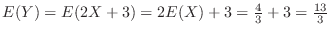
注 : 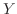 の確率密度関数を求めたので,直接
の確率密度関数を求めたので,直接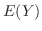 を
を
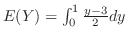 で求めることもできる.
で求めることもできる.
最後に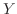 の分散を求める.ここで
の分散を求める.ここで
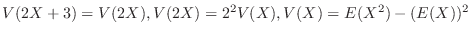 に注意すると
に注意すると 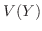 を求めるには
を求めるには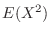 を求めればよいことが分かる.
を求めればよいことが分かる.
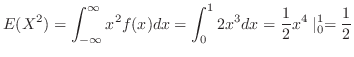
![$\displaystyle V(Y) = V(2X+3) = 4V(X) = 4[E(X^2) - (E(X))^2] = 4[\frac{1}{2} - (\frac{2}{3})^2] = \frac{2}{9}$](img513.png)
(b)
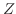 の確率密度関数
の確率密度関数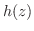 を求めるには
を求めるには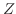 の分布関数
の分布関数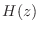 について調べ,
について調べ,
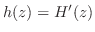 の関係を用いる.
の関係を用いる.
 の分布関数
の分布関数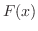 は
は
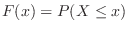 ,
,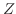 の分布関数
の分布関数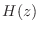 は
は
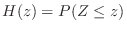 で与えられるので,
で与えられるので,
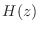 |
 |
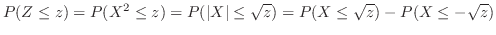 |
|
 |
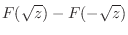 |
 の確率密度関数
の確率密度関数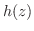 は,
は,
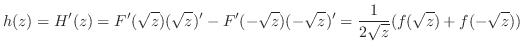
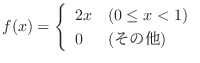
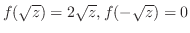 .したがって,
.したがって,
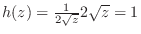 .
.
次に期待値を求める.
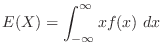 で与えられるので,
で与えられるので,
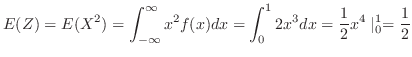
最後に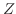 の分散を求める.
の分散を求める.
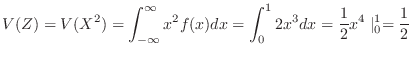
![$\displaystyle V(Y) = V(2X+3) = 4V(X) = 4[E(X^2) - (E(X))^2] = 4[\frac{1}{2} - (\frac{2}{3})^2] = \frac{2}{9}$](img513.png)
3.
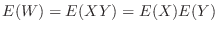
 は1つのさいころを投げたとき出る目の値であるから,その期待値
は1つのさいころを投げたとき出る目の値であるから,その期待値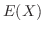 は
は
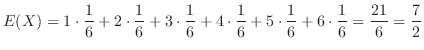
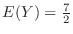 となるので,求める期待値
となるので,求める期待値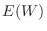 は
は
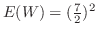 となる.
となる.
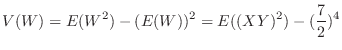
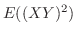 を求めればよい.ここで
を求めればよい.ここで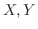 は独立であることに注意すると
は独立であることに注意すると
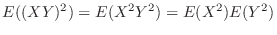
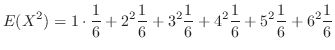
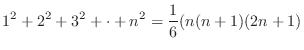
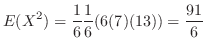
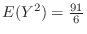 となるので,求める
となるので,求める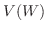 は
は
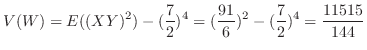
演習問題4.1

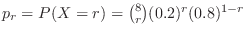 より
より

2. プラモデルを取り出す試行はベルヌーイ試行.
 を部品がかけているプラモデルのセットの数とすると,
を部品がかけているプラモデルのセットの数とすると,
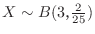 .よって,選んだ3セットが全て完全なセットである確率は
.よって,選んだ3セットが全て完全なセットである確率は
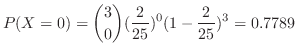
3.  を注射のあと一定期間生存できずに死亡するねずみの数とすると,
を注射のあと一定期間生存できずに死亡するねずみの数とすると,
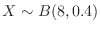 となり,Iで求めた確率分布が使える.
となり,Iで求めた確率分布が使える.
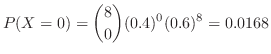
(b) 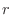 を95%以上の確率で生存できないねずみの数となるとすると,
を95%以上の確率で生存できないねずみの数となるとすると, の分布関数
の分布関数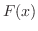 は
は
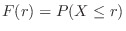 |
 |
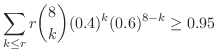 |
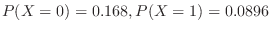 より,
より,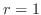 となり,
となり,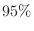 で生存できるねずみの数は7匹以上となる.
で生存できるねずみの数は7匹以上となる.
演習問題4.2
1.  を1日における交通事故の数とすると,交通事故という事象は,ポワソン過程である。よって,一日での事象の平均発生回数
を1日における交通事故の数とすると,交通事故という事象は,ポワソン過程である。よって,一日での事象の平均発生回数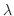 は0.8となる。
は0.8となる。
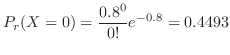
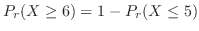
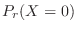 |
 |
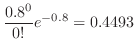 |
|
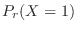 |
 |
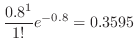 |
|
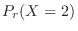 |
 |
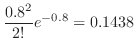 |
|
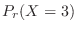 |
 |
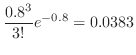 |
|
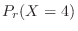 |
 |
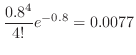 |
|
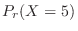 |
 |
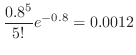 |
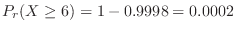
2.
 を放射性物質から1秒間に放出される粒子の数とすると,粒子の放出はポワソン過程である。よって,一秒間での事象の平均発生回数
を放射性物質から1秒間に放出される粒子の数とすると,粒子の放出はポワソン過程である。よって,一秒間での事象の平均発生回数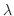 は3となる。これより,
一秒間に0個の粒子が放出される確率は
は3となる。これより,
一秒間に0個の粒子が放出される確率は
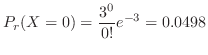
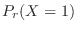 |
 |
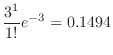 |
|
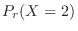 |
 |
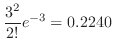 |
|
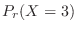 |
 |
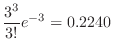 |
|
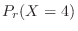 |
 |
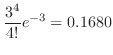 |
|
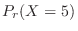 |
 |
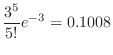 |
|
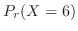 |
 |
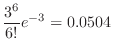 |
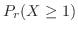 で与えられ,
で与えられ,
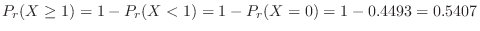
3.  をテープの傷の数とおくと,300m中の傷の数の平均は6となり
をテープの傷の数とおくと,300m中の傷の数の平均は6となり
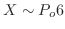 .よって300mの長さのテープ一巻中に傷が全くない確率は
.よって300mの長さのテープ一巻中に傷が全くない確率は
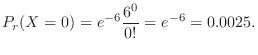
演習問題4.3
1.
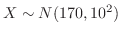 より,
より,
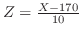 とおくと,
とおくと,
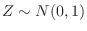 となる。
となる。
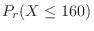 |
 |
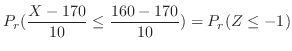 |
|
 |
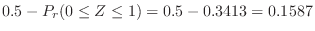 |
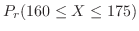 |
 |
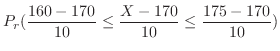 |
|
 |
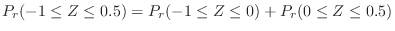 |
||
 |
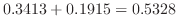 |
2.
(a)
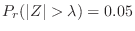 を満たす
を満たす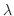 を求める。標準正規分布表により,
を求める。標準正規分布表により,
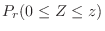 の値が与えられている。そこで,
の値が与えられている。そこで,
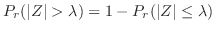
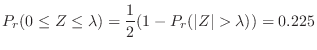
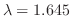 を得る。
を得る。
(b)
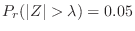 を満たす
を満たす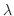 を求める。標準正規分布表により,
を求める。標準正規分布表により,
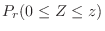 の値が与えられている。そこで,
の値が与えられている。そこで,
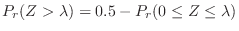
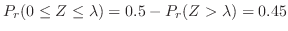
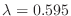 を得る。
を得る。
3.
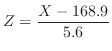
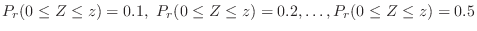
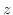 を求めると,
を求めると,
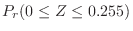 |
 |
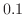 |
|
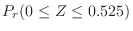 |
 |
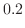 |
|
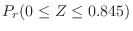 |
 |
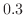 |
|
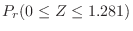 |
 |
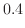 |
|
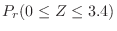 |
 |
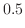 |
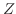 の値を次のように分ければよい。
の値を次のように分ければよい。
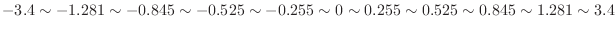
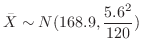
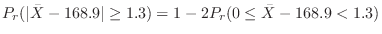
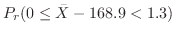 |
 |
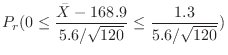 |
|
 |
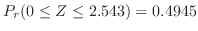 |
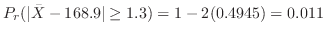
4.
(a)
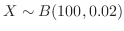 より,期待値
より,期待値
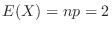 となり,ポワソン分布で近似できる。
となり,ポワソン分布で近似できる。
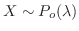 ,
,
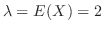 より,
より,
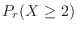 |
 |
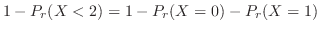 |
|
 |
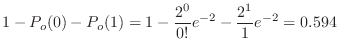 |
(b)
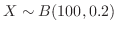 より,期待値
より,期待値
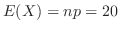 となり,正規分布で近似できる。
となり,正規分布で近似できる。
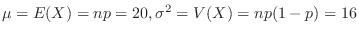 より,
より,
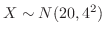 。これより
。これより
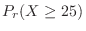 |
 |
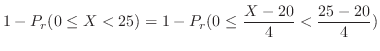 |
|
 |
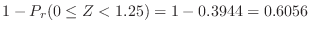 |
(c)  を1の目の出る回数とすると,
を1の目の出る回数とすると,
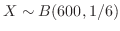 の2項分布に従う。そこで,1の目の出る回数
の2項分布に従う。そこで,1の目の出る回数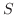 が90回以上100回以下である確率を求めると
が90回以上100回以下である確率を求めると

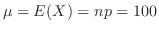 ,
,
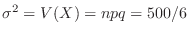 より,
より,
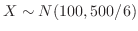 の正規分布で近似できることが分かる。正規分布を用いると
の正規分布で近似できることが分かる。正規分布を用いると
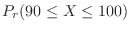 |
 |
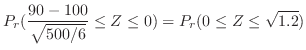 |
|
 |
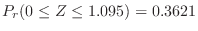 |
(d)  を表の目の出る回数とすると,
を表の目の出る回数とすると,
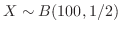 の2項分布に従う。そこで,表の出る回数が40以上60以下の確率を求めると
の2項分布に従う。そこで,表の出る回数が40以上60以下の確率を求めると
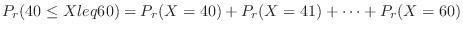
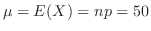 ,
,
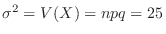 より,
より,
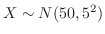 の正規分布で近似できることが分かる。正規分布を用いると
の正規分布で近似できることが分かる。正規分布を用いると
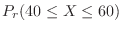 |
 |
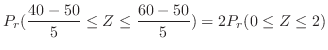 |
|
 |
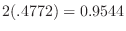 |
演習問題4.4
1.
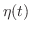 |
 |
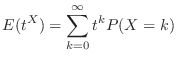 |
|
 |
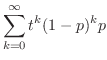 |
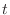 について微分すると,
について微分すると,
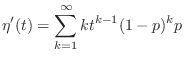
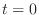 とおくと
とおくと
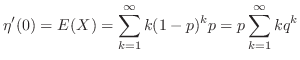
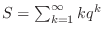 とおき,
とおき,
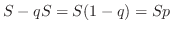 を求めると,
を求めると,
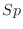 |
 |
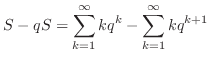 |
|
 |
 |
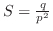 となり,
となり,
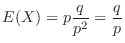
(b)  をはじめて勝つ直前までの試合回数とおくと,
をはじめて勝つ直前までの試合回数とおくと,
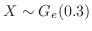 .よってはじめて勝つまでの平均試合数は
.よってはじめて勝つまでの平均試合数は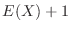 より
より
演習問題4.5
1.  を当たりくじの数とおくと,
を当たりくじの数とおくと,
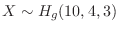 .よって3本くじを引いて,そのうち2本が当たる確率は
.よって3本くじを引いて,そのうち2本が当たる確率は
演習問題4.6
II.
(a)  を通話時間とおくと,
を通話時間とおくと,
![]() .また
.また
![]() より
より
![]() となるので
となるので
![]() .よって通話が4分以内に終わる確率は
.よって通話が4分以内に終わる確率は
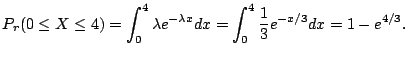
(b) その人が通話をはじめてから2分が経過しているとき,その後4分以内に終わる確率は
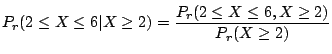 |
|||
 |
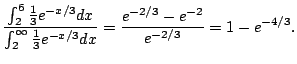 |
演習問題4.7
I.  が密度関数になるには,
が密度関数になるには,
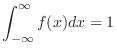
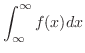 |
 |
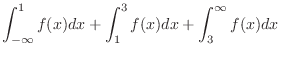 |
|
 |
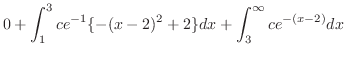 |
||
 |
![$\displaystyle ce^{-1}\left[-\frac{1}{3}(x-2)^{3} + 2x \right]_{1}^{3} - \left[ce^{-(x-2)}\right]_{3}^{\infty}$](img667.png) |
||
 |
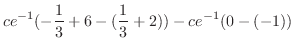 |
||
 |
2. 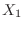 をA型の人の数,
をA型の人の数,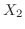 をB型の人の数,
をB型の人の数,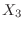 をAB型の人の数,
をAB型の人の数,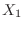 をO型の人の数とすると,
をO型の人の数とすると,
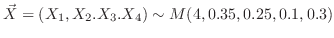 .よって
.よって
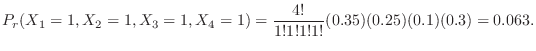
3.
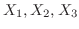 を3人の通話時間とおくと,
を3人の通話時間とおくと,
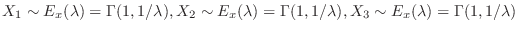 .ここで
.ここで
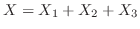 とおくと
とおくと は3人の通話時間の合計を表わす.言い換えると待ち時間を表わし,
は3人の通話時間の合計を表わす.言い換えると待ち時間を表わし,
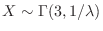 .また
.また
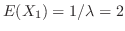 より
より
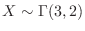 .よって10分以上待たなければならない確率は
.よって10分以上待たなければならない確率は
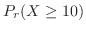 |
 |
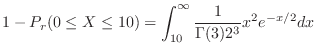 |
|
 |
![$\displaystyle 1 - \frac{1}{16}\int_{0}^{10}x^2 e^{-x/2}dx = 1 - [-2x^2 e^{-x/2}\mid_{0}^{10} + 4\int_{0}^{10}xe^{-x/2}dx ]$](img682.png) |
||
 |
![$\displaystyle 1 - \frac{1}{16}[-200e^{-5} + 4(-2xe^{-x/2}\mid_{0}^{10} + 2\int_{0}^{10}e^{-x/2}dx)]$](img683.png) |
||
 |
![$\displaystyle 1 - \frac{1}{16}[-200e^{-5} -80e^{-5} - 16e^{-x/2}\mid_{0}^{10}]$](img84.gif) |
||
 |
![$\displaystyle 1 - \frac{1}{16}[-296e^{-5} + 16] = \frac{296 e^{-5}}{16} = 0.1246$](img85.gif) |
演習問題5.1
1. 正規母集団
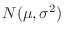 から無作為で抽出した標本
から無作為で抽出した標本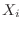 は,母集団と同じ正規分布に従っていると考えられる。よって,
は,母集団と同じ正規分布に従っていると考えられる。よって,
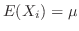 である。これより,
である。これより,
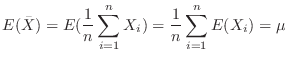
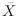 は母平均を推測するのに適当な統計量である。
は母平均を推測するのに適当な統計量である。
次に,
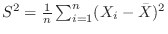 と定義すると,
と定義すると,
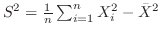 となる。
となる。
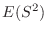 |
 |
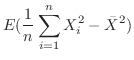 |
|
 |
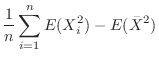 |
||
 |
![$\displaystyle \frac{1}{n}\sum_{i=1}^{n}[V(X_{i}) + (E(X_{i}))^{2}] - [V(\bar{X}) + (E(\bar{X}))^{2}$](img690.png) |
||
 |
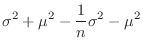 |
||
 |
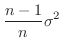 |
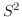 は母分散を推測するのに適当な統計量ではない。
は母分散を推測するのに適当な統計量ではない。
演習問題5.2
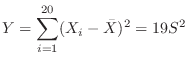
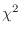 分布に従う。したがって,
分布に従う。したがって,
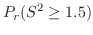 |
 |
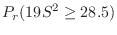 |
|
 |
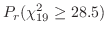 |
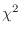 分布表を用いると,
分布表を用いると,
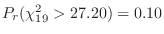 で
で
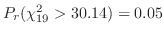 より,
より,