Next: 2次元確率分布(Two dimensional probability distribution) Up: 確率変数 Previous: 確率変数 目次
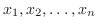 なる
なる 個の値をとる変数
個の値をとる変数 に対して,
に対して,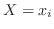 なる確率
なる確率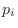 が与えられているとき,
が与えられているとき, を確率変数という.
を確率変数という.
 とそれに対応する確率
とそれに対応する確率
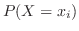 との対応関係を確率分布という.
との対応関係を確率分布という.
 の値がある値
の値がある値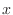 までとる確率を
までとる確率を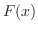 で表し,確率変数
で表し,確率変数 の分布関数という.つまり,分布関数は
の分布関数という.つまり,分布関数は
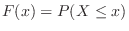 で与えられる.
で与えられる.
確率変数 のとる値が有限個または,無限個であっても自然数で番号が付けられる場合,確率変数
のとる値が有限個または,無限個であっても自然数で番号が付けられる場合,確率変数 は離散型(discrete)であるという.また,確率変数
は離散型(discrete)であるという.また,確率変数 がある区間内の全ての実数を取り得る場合,連続型(continuous)であるという.
がある区間内の全ての実数を取り得る場合,連続型(continuous)であるという.
離散型の場合
確率変数 のとる値を
のとる値を
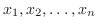 とし,各事象
とし,各事象
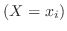 の確率を
の確率を
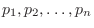 とするとき,
とするとき,
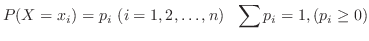
 の確率分布
の確率分布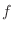 は
は
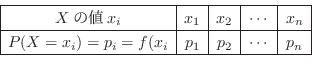
 のとる値を
のとる値を
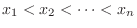 とするとき,その分布関数
とするとき,その分布関数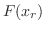 は次のように求められる.
は次のように求められる.
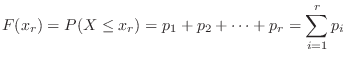
確率分布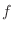 と分布関数
と分布関数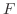 は次の性質をもつ.
は次の性質をもつ.
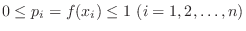
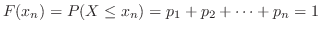
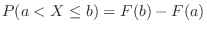
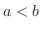
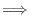
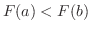
連続型の場合
確率変数 が連続的な値をとるとき,事象
が連続的な値をとるとき,事象
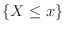 の確率が連続関数
の確率が連続関数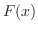 によって,
によって,
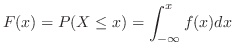
で与えられるとき,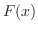 を
を の分布関数といい,
の分布関数といい,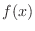 を確率密度関数という.
を確率密度関数という.
(1) 男児と女児の出生率が等しいと仮定して,4児を持つ家庭の確率変数 の値と確率分布
の値と確率分布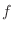 を求めよ.
を求めよ.
(2) 1つの袋に赤玉4個と白玉6個が入っている.同時に3個の球を取り出す場合,赤玉の個数を表わす確率変数 と確率分布
と確率分布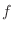 を求め,そのグラフをかこう.また,
を求め,そのグラフをかこう.また,
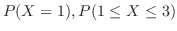 を求めよう.
を求めよう.
3. 与えられた
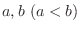 に対して,関数
に対して,関数
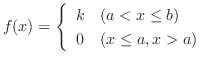
が与えられている.
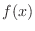 が確率密度関数であるためには,定数
が確率密度関数であるためには,定数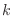 はどのような値であるか.
はどのような値であるか.
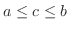 である
である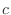 に対して
に対して
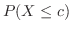 を求めよ.
を求めよ.
4. 確率密度が
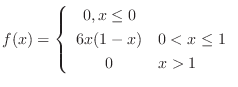
で与えられている.
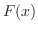 を求めよ.
を求めよ.
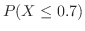 ,
,
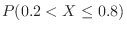 を求めよ.
を求めよ.
5. 関数
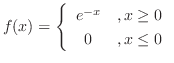
が与えられている.
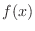 は確率密度関数を与えることを示せ.
は確率密度関数を与えることを示せ.
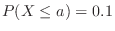 ,
,
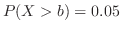 であるような
であるような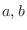 を求めよ.
を求めよ.