Next: 多次元確率分布(Multidimensional probability distribution) Up: 確率変数 Previous: 2次元確率分布(Two dimensional probability distribution) 目次
 に対して,次の式で定義される値
に対して,次の式で定義される値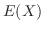 を
を の平均値(Mean)または期待値(Expectation)といい,
の平均値(Mean)または期待値(Expectation)といい,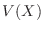 を
を の分散という。
の分散という。
離散型の場合
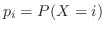
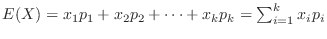
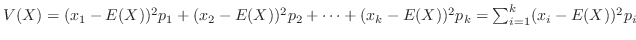
連続型の場合
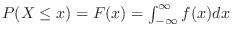
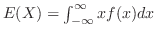
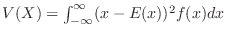
![]() の期待値と分散
の期待値と分散
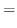 |
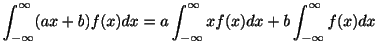 |
||
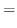 |
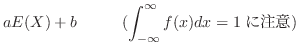 |
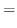 |
![$\displaystyle \int_{-\infty}^{\infty}[(ax + b) - (aE(x) + b)]^2 f(x)dx = \int_{-\infty}^{\infty}a^2(x-E(x))^2 f(x)dx$](img14.gif) |
||
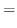 |
1.
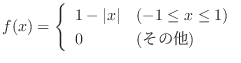
のとき次の問いに答えよう.
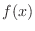 は確率密度関数であることを示そう.
は確率密度関数であることを示そう.
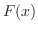 を求めよう.
を求めよう.
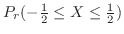 を求めよう.
を求めよう.
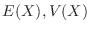 を求めよう.
を求めよう.
2. 1つのサイコロを,3回投げるとき,1の目が出る回数を とする.
とする.
 の確率分布を求めよう.
の確率分布を求めよう.
 の平均と標準偏差を求めよう.
の平均と標準偏差を求めよう.
 を標準化した確率変数
を標準化した確率変数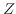 を求め,更に,
を求め,更に,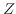 の確率分布を求めよう.
の確率分布を求めよう.
3. Bernoulliの定理を利用して,次の確率を求めよう.
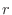 が
が
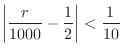
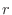 が,
が,
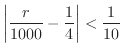
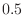 との差が
との差が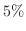 以内である確率が
以内である確率が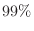 以上であるようにするには,何回以上投げればよいか.
以上であるようにするには,何回以上投げればよいか.