Next: 幾何分布(Geometric distribution) Up: 理論分布 Previous: 正規分布(Normal distribution) 目次
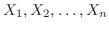 が互いに独立で正規分布
が互いに独立で正規分布
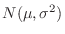 に従っているとすると,
に従っているとすると,
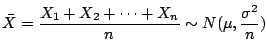
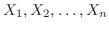 が互いに独立で同じ分布にに従っているとする.このとき,
が互いに独立で同じ分布にに従っているとする.このとき, が十分大きければ
が十分大きければ
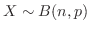 のとき,十分大きな
のとき,十分大きな に対して
に対して
 は近似的に
は近似的に
1.
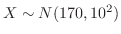 のとき,次の確率を求めよう.
のとき,次の確率を求めよう.
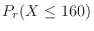
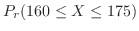
2.
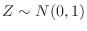 のとき,次の式を満たす
のとき,次の式を満たす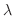 を求めよ.
を求めよ.
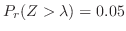
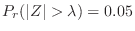
3. 全国の20才に男子の身長は正規分布
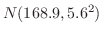 に従うものとする.
に従うものとする.
4. 2項分布,ポワソン分布,正規分布について,次のことがいえます.
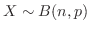 のとき,
のとき,
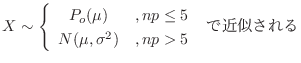
このことを用いて次の質問に答えよう.
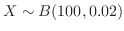 のとき,
のとき,
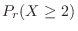 を求めよ.
を求めよ.
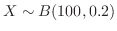 のとき,
のとき,
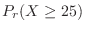 を求めよ.
を求めよ.
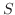 が90回以上100回以下である確率を近似せよ.
が90回以上100回以下である確率を近似せよ.