Next: 超幾何分布(Hypergeometric distribution) Up: 理論分布 Previous: 正規分布の応用(Application of normal distribution) 目次
繰返し独立に試行を行うとき,注目している事象が初めて起こる直前までの試行回数を とし,
とし,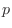 を注目している事象が起こる確率とすると,注目している事象が
を注目している事象が起こる確率とすると,注目している事象が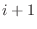 回目に起こる確率は,
回目に起こる確率は,
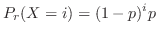
となる。このとき,確率変数 は幾何分布(Geometric distribution)
は幾何分布(Geometric distribution)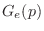 に従うといい,
に従うといい,
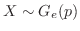
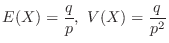
期待値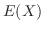 を求める一つの方法に,母関数(generating function)を用いる方法がある。
を求める一つの方法に,母関数(generating function)を用いる方法がある。
離散型の場合
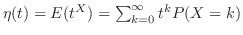 とおくと,
とおくと,
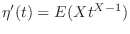 より,
より,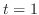 のとき,
のとき,
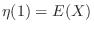 となる。よって,期待値は
となる。よって,期待値は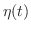 が求まれば微分することにより求めることができる。
が求まれば微分することにより求めることができる。
連続型の場合
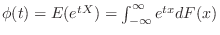 とおき,
とおき,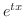 を整級数で置き換えると,
を整級数で置き換えると,
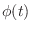 |
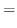 |
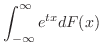 |
|
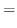 |
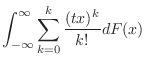 |
||
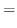 |
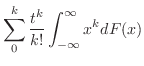 |
||
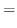 |
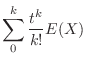 |
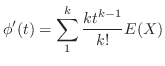
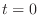 とおくと,
とおくと,
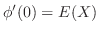
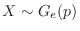 のとき,
のとき,
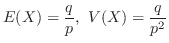
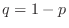 .
.