Next: 正規分布(Normal distribution) Up: 理論分布 Previous: 2項分布(Binomial distribution) 目次
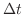 における事象の発生確率は
における事象の発生確率は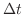 に比例して小さくなっている。
に比例して小さくなっている。
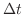 の間に事象が2回以上発生する確率は無視できる。
の間に事象が2回以上発生する確率は無視できる。
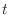 の間に当該事象が発生する平均発生回数
の間に当該事象が発生する平均発生回数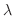 がおおむね5以下である。
がおおむね5以下である。
 をポワソン過程における事象の発生回数とすると,
をポワソン過程における事象の発生回数とすると,
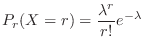
となり,
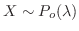 と表す。ただし,
と表す。ただし,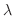 はポワソン過程における事象の平均発生回数。
はポワソン過程における事象の平均発生回数。
ポワソン過程には,テープの傷,交換台にかかってくる電話,電球の破損,タクシー待ちなどがある。
1. 交通事故による死亡者が1日平均0.8人であるとき,次の確率はいくらか.
2. ある放射性物質から1秒間に放出される粒子の数は平均して3個である.1秒間に0,1,2,3,4,5,6個の粒子が放出される確率を求めよ.1秒間に少なくとも1個の粒子が放出される確率はいくらか.
3. ある磁気テープには,平均して100mあたりに2個の傷があることが分かっている.このとき,300mの長さのテープ一巻中に傷が全くない確率を求めよ.