Next: ポワソン分布(Poison distribution) Up: 理論分布 Previous: 理論分布 目次
1回の試行において,ある事象 が発生する確率を
が発生する確率を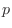 とする。n回のベルヌーイ試行列において,ちょうど
とする。n回のベルヌーイ試行列において,ちょうど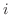 回事象
回事象 が発生する確率は
が発生する確率は
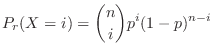
で表され,このとき の確率分布を2項分布(Binomial distribution)といい,
の確率分布を2項分布(Binomial distribution)といい,
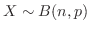 と表す.
と表す.
1. 2項分布
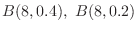 の確率分布を求めよ.
の確率分布を求めよ.
2. ある会社で製造したプラモデルは25セット中2セットの割合で部品がかけているとする.客が任意に3セット選ぶとき,いずれも完全なセットである確率を求めよ.
3. ある試薬をネズミに注射すると一定期間のうちに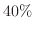 が死亡するという.8匹のネズミにその試薬を注射した場合,
が死亡するという.8匹のネズミにその試薬を注射した場合,
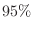 の確率で,8匹のうち何匹以上が生存するということができるか.
の確率で,8匹のうち何匹以上が生存するということができるか.