Next: 部分空間と次元 Up: ベクトル空間 Previous: 内積空間 目次 索引
1.
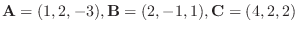 について,
について,
2. 点(1,0,1)を通り,
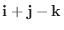 と
と
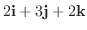 によって作られる平面に平行な平面を求めよ.
によって作られる平面に平行な平面を求めよ.
3. 2点
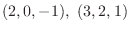 を通り平面
を通り平面
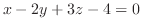 に垂直な平面の方程式を求めよ.
に垂直な平面の方程式を求めよ.
4.
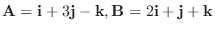 を2辺とする三角形の面積を求めよ.
を2辺とする三角形の面積を求めよ.
5.
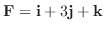 のとき, 点
のとき, 点 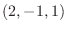 のまわりの力F のモーメントベクトルを求めよ.
のまわりの力F のモーメントベクトルを求めよ.
6. 剛体が直線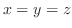 のまわりを角速度ベクトル
のまわりを角速度ベクトル
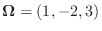 で回転しているとき, 剛体内の点
で回転しているとき, 剛体内の点 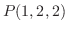 の速度を求めよ.
の速度を求めよ.
7. 3つのベクトル A,B,C の作る平行六面体の体積は, スカラー三重積
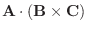
8.
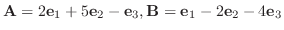 で
で
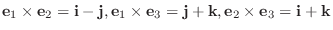 のとき,
のとき,
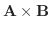 を求めよ.
を求めよ.
9.
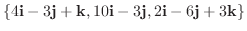 は1次独立か1次従属か調べよ.
は1次独立か1次従属か調べよ.
10. 次の関数はどの区間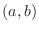 でも1次独立であることを示せ.
でも1次独立であることを示せ.
11. 幾何ベクトル A, B が1次独立であるための必要十分条件は
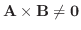 であることを示せ.
であることを示せ.