Next: 行列と行列式 Up: ベクトル空間 Previous: 1次独立と1次従属 目次 索引
1.
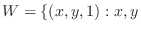 実数
実数 は
は 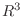 の部分空間か調べよ.
の部分空間か調べよ.
2.
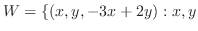 実数
実数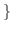 は
は 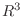 の部分空間であることを証明せよ.
の部分空間であることを証明せよ.
3.
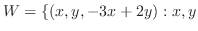 実数
実数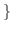 の基底を求めよ.また
の基底を求めよ.また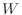 は何次元か.
は何次元か.
4. 次のベクトルの組は3次元ベクトル空間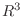 の基底をなすことを示せ.
の基底をなすことを示せ.
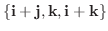
5. 次の関数で生成される部分空間の次元を求めよ.
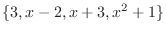
6.
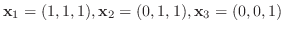 から正規直交系を作れ.
から正規直交系を作れ.
7. 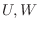 をベクトル空間
をベクトル空間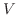 の部分空間とするとき, 次元公式が成り立つことを示せ.
の部分空間とするとき, 次元公式が成り立つことを示せ.
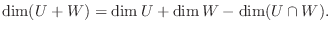
8. 4個以上の3次元空間のベクトルの組は1次従属であることを示せ.