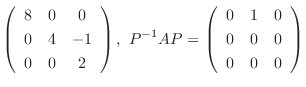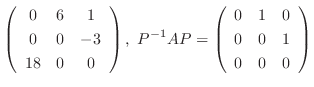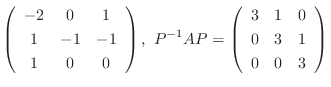Next: 索引 Up: 線形代数学入門演習書 Previous: ベキ零行列の標準形 目次 索引
1.
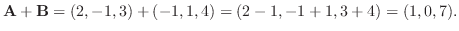
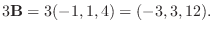
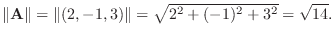
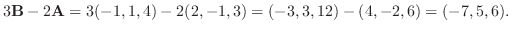
2.
3. 幾何ベクトルは空間のベクトルと同一視できるので演習問題 1-2-1.5 を参照.
4. 幾何ベクトルは空間のベクトルと同一視できるので演習問題 1-2-1.5 を参照.
(1)
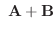 |
 |
 |
|
 |
 |
(2)
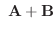 |
 |
 |
|
 |
 |
||
 |
 |
(3)
 |
 |
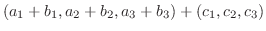 |
|
 |
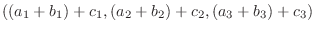 |
||
 |
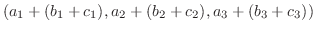 |
||
 |
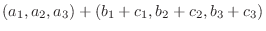 |
||
 |
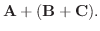 |
(4)
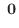 |
 |
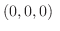 とすると とすると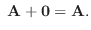 |
(5)
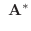 |
 |
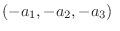 とすると とすると |
|
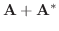 |
 |
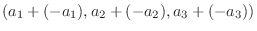 |
|
 |
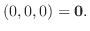 |
(6)
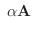 |
 |
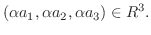 |
(7)
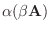 |
 |
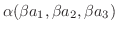 |
|
 |
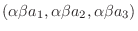 |
||
 |
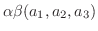 |
||
 |
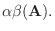 |
(8)
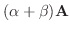 |
 |
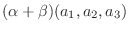 |
|
 |
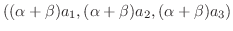 |
||
 |
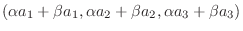 |
||
 |
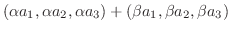 |
||
 |
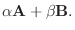 |
(9)
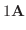 |
 |
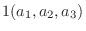 |
|
 |
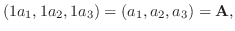 |
||
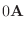 |
 |
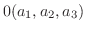 |
|
 |
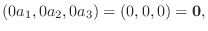 |
||
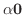 |
 |
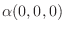 |
|
 |
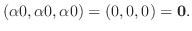 |
6.
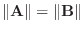 のとき
のとき
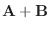 は
は 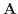 と
と 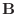 を2辺とするひし形の対角線ベクトル.よって
を2辺とするひし形の対角線ベクトル.よって 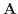 と
と 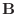 の作る角を2等分するベクトル.
の作る角を2等分するベクトル.
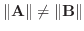 のときは,
のときは, 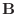 をスカラー倍して,
をスカラー倍して,
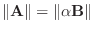 とすると,
とすると,
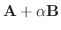 は
は 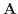 と
と 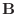 の作る角を2等分するベクトルとなる.
7.
の作る角を2等分するベクトルとなる.
7.
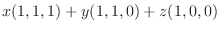 |
 |
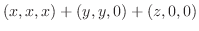 |
|
 |
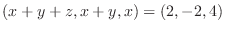 |
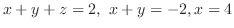 .この式を後ろから順に解くと
.この式を後ろから順に解くと
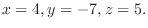
1.
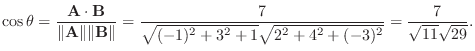
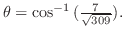
(d) 単位ベクトルはそれ自身をその大きさで割ることで得られるから
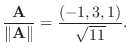
2. 直交系とは互いのベクトルが直交している集合.
正規直交系とはそれぞれが単位ベクトルで直交系をなしているもの.
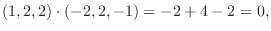
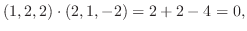
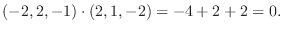
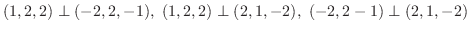 . また正規直交系に直すと
. また正規直交系に直すと
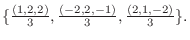
3.平面上に任意の点 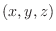 をとり, 点
をとり, 点 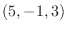 を始点とし点
を始点とし点 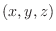 を終点とするベクトルを考える.このベクトル
を終点とするベクトルを考える.このベクトル
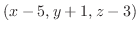 は求める平面上にあるので, 法ベクトル
は求める平面上にあるので, 法ベクトル 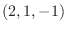 と直交する.よってその内積は零である.これより
と直交する.よってその内積は零である.これより
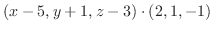 |
 |
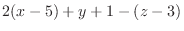 |
|
 |
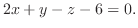 |
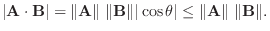
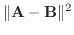 |
 |
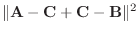 |
|
 |
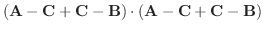 |
||
 |
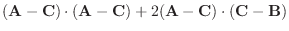 |
||
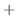 |
 |
||
 |
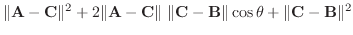 |
||
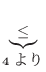 |
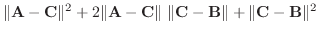 |
||
 |
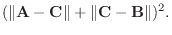 |
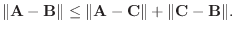
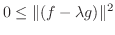 |
 |
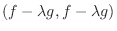 |
|
 |
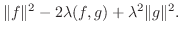 |
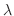 についての2次式で0より大きいので, その判別式
についての2次式で0より大きいので, その判別式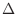 は0以下になる.よって
は0以下になる.よって
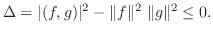
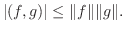
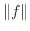 |
 |
![$\displaystyle \{\int_{0}^{2}[\sin{\pi x}]^{2}dx\}^{1/2} = \{\int_{0}^{2}\frac{1 - \cos{2\pi x}}{2}dx \}^{1/2}$](img285.png) |
|
 |
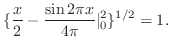 |
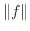 |
 |
![$\displaystyle \{\int_{0}^{2}[\cos{\pi x}]^{2}dx\}^{1/2} = \{\int_{0}^{2}\frac{1 + \cos{2\pi x}}{2}dx \}^{1/2}$](img287.png) |
|
 |
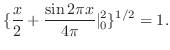 |
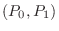 |
 |
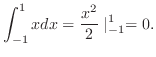 |
|
 |
 |
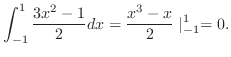 |
|
 |
 |
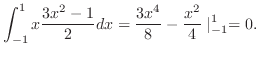 |
1.
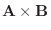 |
 |
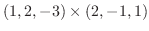 |
|
 |
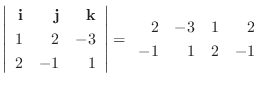 |
||
 |
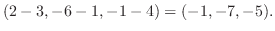 |
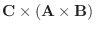 |
 |
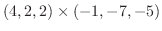 |
|
 |
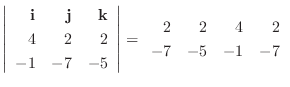 |
||
 |
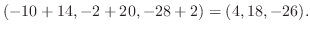 |
 |
 |
 |
|
 |
 |
2.
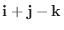 と
と
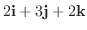 によって作られる平面を
によって作られる平面を 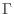 とすると,
とすると, 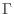 の法ベクトル
の法ベクトル
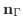 は
は
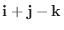 と
と
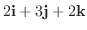 に直交する.よって
に直交する.よって
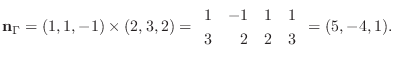
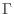 に平行なので
に平行なので
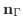 は求める平面に対しても法ベクトルとなる.そこで求める平面上に任意の点
は求める平面に対しても法ベクトルとなる.そこで求める平面上に任意の点 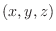 をとると
をとると
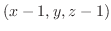 は
は
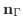 と直交する.よって求める平面の方程式は
と直交する.よって求める平面の方程式は
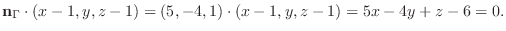
3.求める平面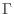 は平面
は平面
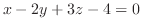 に垂直であるから平面
に垂直であるから平面
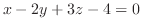 の法ベクトル
の法ベクトル
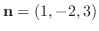 は求める平面上にあると考えることができる.また求める平面は2点
は求める平面上にあると考えることができる.また求める平面は2点
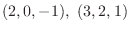 を通るのでこの2点を結ぶベクトルを作ると
を通るのでこの2点を結ぶベクトルを作ると
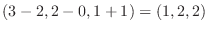 となり, このベクトルも求める平面上にあることが分かる.そこでこのふたつのベクトルの外積をとると求める平面
となり, このベクトルも求める平面上にあることが分かる.そこでこのふたつのベクトルの外積をとると求める平面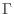 の法ベクトル
の法ベクトル
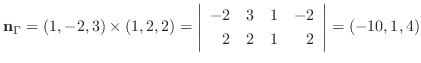
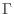 上に任意の点
上に任意の点 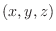 をとり
をとり 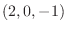 と結ぶと
と結ぶと
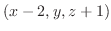 は
は
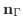 と直交する.よって求める平面の方程式は
と直交する.よって求める平面の方程式は
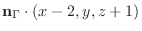 |
 |
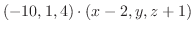 |
|
 |
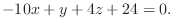 |
4.三角形の面積は A,Bを2辺とする平行四辺形の半分であるから,
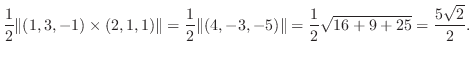
7.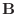 と
と 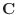 の作る面の面積は
の作る面の面積は
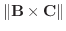 .また
.また
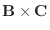 とA の間の角を
とA の間の角を 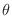 とすると,
とすると,
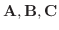 の作る平行六面体の高さは
の作る平行六面体の高さは
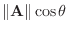 .よって
.よって
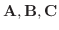 の作る平行六面体の面積は
の作る平行六面体の面積は
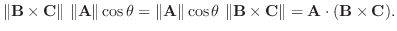
8. それ自身の外積は0, かける順序を変えると符号が反対になることに注意.
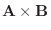 |
 |
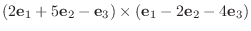 |
|
 |
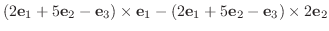 |
||
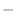 |
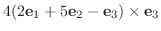 |
||
 |
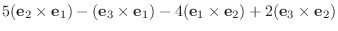 |
||
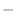 |
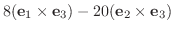 |
||
 |
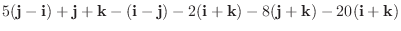 |
||
 |
 |
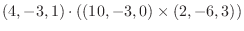 |
 |
 |
|
 |
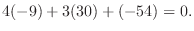 |
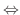 スカラー3重積が0でない)より1次従属.
スカラー3重積が0でない)より1次従属.
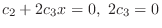
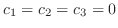 を得るので
を得るので
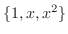 は1次独立.
は1次独立.
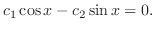
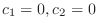 となるので1次独立.
となるので1次独立.
11.
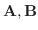 が1次独立ならば,
が1次独立ならば,
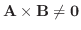 を示す.(対偶を用いて
を示す.(対偶を用いて
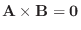 のとき
のとき
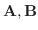 が1次従属であることを示す.)
が1次従属であることを示す.)
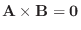 とするとA とB は平行.つまり
とするとA とB は平行.つまり
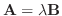 となるある
となるある
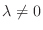 が存在.書き直すと
が存在.書き直すと
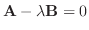
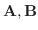 は1次従属.
は1次従属.
次に
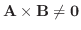 ならば,
ならば,
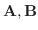 が1次独立を示す.(対偶を用いて
が1次独立を示す.(対偶を用いて
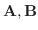 が1次従属のとき,
が1次従属のとき,
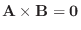 を示す.)
を示す.)
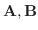 が1次従属ならば, 0でない
が1次従属ならば, 0でない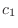 または
または 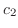 に対して,
に対して,
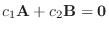
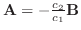 .つまり
.つまり 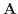 と
と 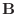 は平行.したがって,
は平行.したがって,
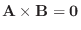 .
.
1.
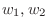 を
を 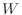 の元とすると,
の元とすると,
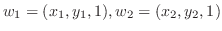 と表せる.部分空間になるためには和とスカラー倍が閉じていれば良いのでまず和を調べてみる.
と表せる.部分空間になるためには和とスカラー倍が閉じていれば良いのでまず和を調べてみる.
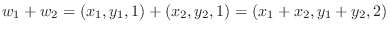 となり
となり 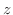 成分が1でないので
成分が1でないので
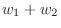 は
は 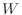 の元でない.よって
の元でない.よって 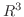 の部分空間でない
の部分空間でない
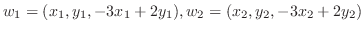
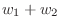 |
 |
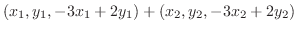 |
|
 |
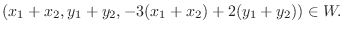 |
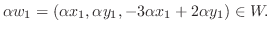
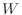 は
は 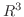 の部分空間である.
の部分空間である.
3.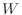 の任意のベクトルを
の任意のベクトルを 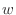 とすると,
とすると,
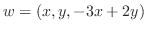 .
. 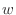 を i, j, kを用いて表すと,
を i, j, kを用いて表すと,
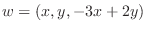 |
 |
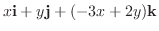 |
|
 |
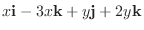 |
||
 |
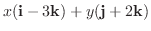 |
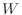 に含まれるすべてのベクトルは, i - 3k とj + 2k の1次結合.またi - 3k とj + 2k は互いに1次独立なので, i - 3k とj + 2k は
に含まれるすべてのベクトルは, i - 3k とj + 2k の1次結合.またi - 3k とj + 2k は互いに1次独立なので, i - 3k とj + 2k は 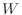 の基底となる.よって
の基底となる.よって
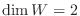 .
.
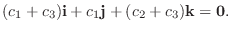
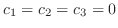 .つまり1次独立.
.つまり1次独立.
次に
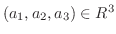 のとき
のとき
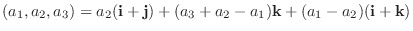
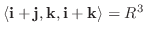 .
.
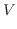 |
 |
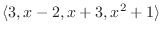 |
|
 |
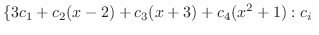 実数 実数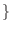 |
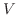 の元を
の元を 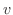 とすると
とすると
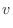 |
 |
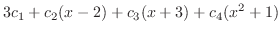 |
|
 |
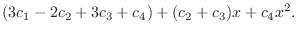 |
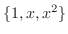 は1次独立であることを示したので,
は1次独立であることを示したので,
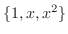 は
は 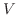 の基底となる.よって
の基底となる.よって
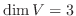 .
.
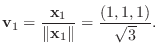
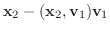 |
 |
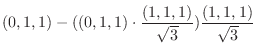 |
|
 |
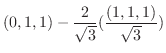 |
||
 |
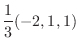 |
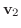 |
 |
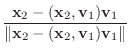 |
|
 |
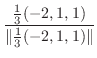 |
||
 |
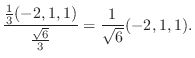 |
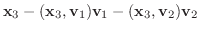 |
 |
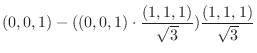 |
|
 |
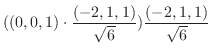 |
||
 |
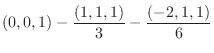 |
||
 |
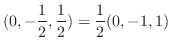 |
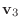 |
 |
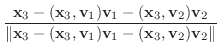 |
|
 |
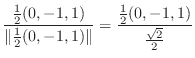 |
||
 |
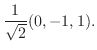 |
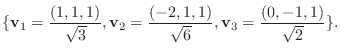
7.
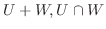 は線形代数学入門例題1.21より
は線形代数学入門例題1.21より 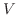 の部分空間である.そこで,
の部分空間である.そこで,
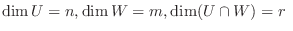 とおき
とおき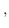
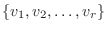 を
を 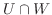 の基底,
の基底,
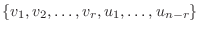 を
を 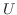 の基底,
の基底,
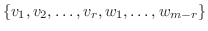 を
を 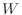 の基底とする.このとき,
の基底とする.このとき,
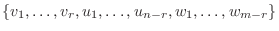
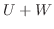 の基底をなすことを示せば
の基底をなすことを示せば
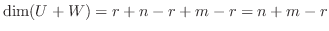
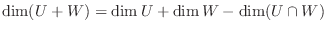
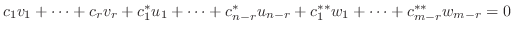 とおくと,
とおくと,
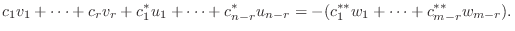
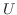 の元であり, 右辺は
の元であり, 右辺は 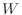 の元であることから共に
の元であることから共に 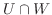 に含まれる.よって
に含まれる.よって
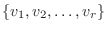 の1次結合で表される.つまり
の1次結合で表される.つまり
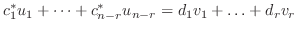
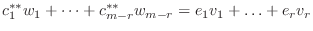
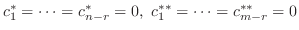 となり,
となり,
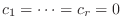 を得る.したがって,
を得る.したがって,
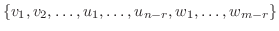
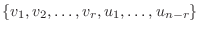 は
は 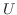 を張り,
を張り,
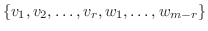 が
が 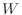 を張るので,
を張るので,
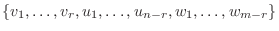
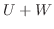 を張るのは明らかである.
を張るのは明らかである.
8.
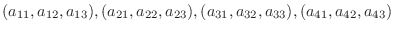 を4個の3次元空間のベクトルとする.線形結合をとり0 とおくと
を4個の3次元空間のベクトルとする.線形結合をとり0 とおくと
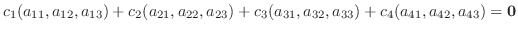
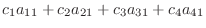 |
 |
0 | |
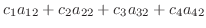 |
 |
0 | |
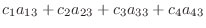 |
 |
0 |
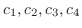 はすべて0の必要はない.つまり
はすべて0の必要はない.つまり
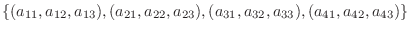
1.
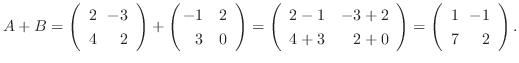
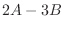 |
 |
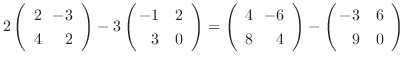 |
|
 |
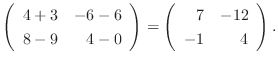 |
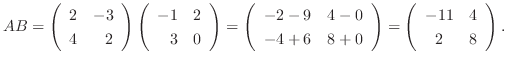
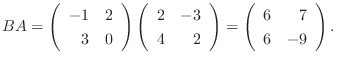
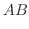 |
 |
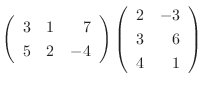 |
|
 |
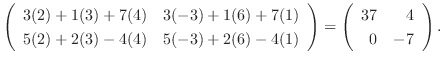 |
||
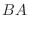 |
 |
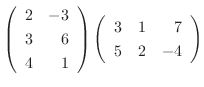 |
|
 |
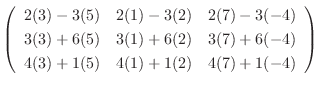 |
||
 |
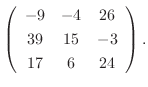 |
 |
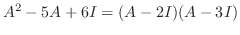 |
||
 |
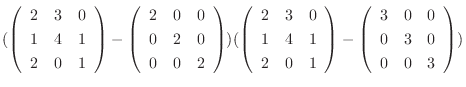 |
||
 |
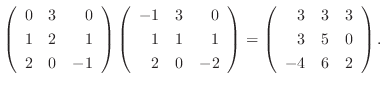 |
4. と
と 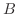 が対称行列ということは,
が対称行列ということは,
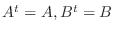 が成り立つということである.また,
が成り立つということである.また, 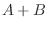 が対称行列であることを示すには
が対称行列であることを示すには
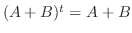 が成り立つことを示せばよい.
が成り立つことを示せばよい.
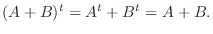
5.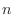 次の対称行列
次の対称行列 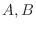 において
において
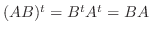 はいつも成り立つ.そこで
はいつも成り立つ.そこで 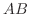 が対称行列になるためには
が対称行列になるためには 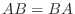 でなければならないことが分かる.また, 一般に行列の積には交換法則が成り立たないので
でなければならないことが分かる.また, 一般に行列の積には交換法則が成り立たないので 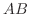 は必ずしも
は必ずしも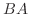 と等しくない.そこで
と等しくない.そこで 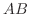 はいつも対称行列かという質問に対する答はたぶんNoであろう.実際,
はいつも対称行列かという質問に対する答はたぶんNoであろう.実際,
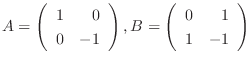 とおくと
とおくと 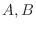 ともに対称行列であるが,
ともに対称行列であるが,
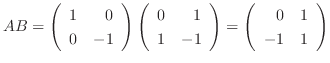
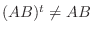 . つまり
. つまり 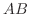 は対称行列でない.
は対称行列でない.
次に 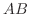 がいつも対称行列になるための必要十分条件を求める.
がいつも対称行列になるための必要十分条件を求める.
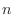 次の対称行列
次の対称行列 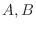 において
において
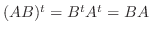 がいつも成り立つので,
がいつも成り立つので, 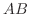 が対称行列になるための必要十分条件は
が対称行列になるための必要十分条件は 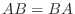 であることを示す.
まず
であることを示す.
まず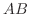 を対称行列とすると
を対称行列とすると
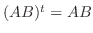 より
より 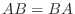 が成り立つ.
が成り立つ.
次に 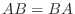 とすると,
とすると,
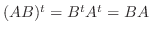 より
より
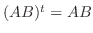 .よって
.よって
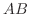 は対称行列.
は対称行列.
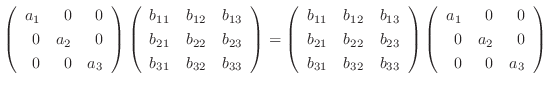
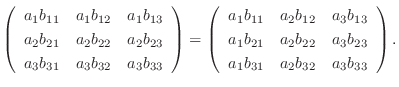
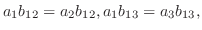
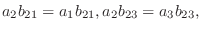
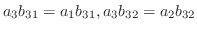
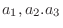 は異なる実数であることに注意すると
は異なる実数であることに注意すると
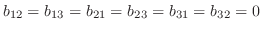
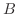 は
は
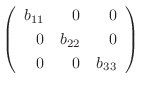
8.
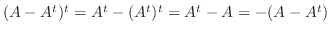 . よって
. よって 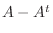 は交代行列である.また
は交代行列である.また
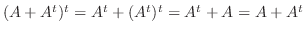 .よって
.よって 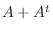 は対称行列である.ここで
は対称行列である.ここで
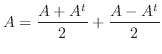
 は対称行列と交代行列の和であることが分かる.つぎに
は対称行列と交代行列の和であることが分かる.つぎに 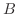 が対称行列,
が対称行列, 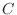 が交代行列で
が交代行列で 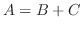 が成り立つとすると
が成り立つとすると
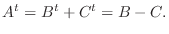
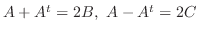 となり
となり
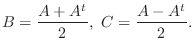
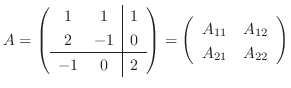
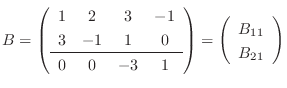
より
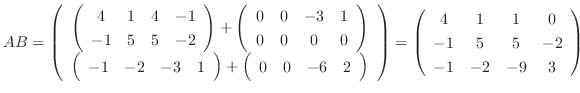
 |
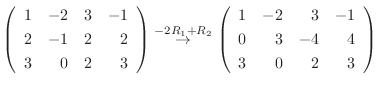 |
||
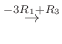 |
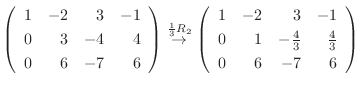 |
||
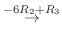 |
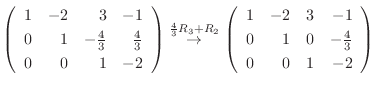 |
||
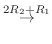 |
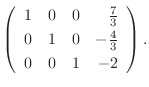 |
2.
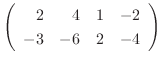 |
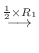 |
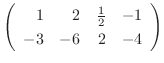 |
|
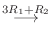 |
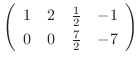 |
||
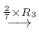 |
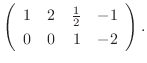 |
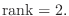
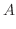 |
 |
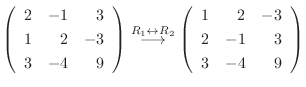 |
|
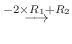 |
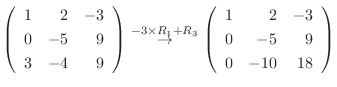 |
||
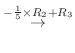 |
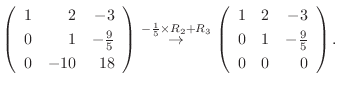 |
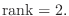
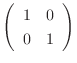 |
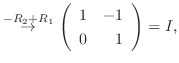 |
||
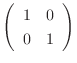 |
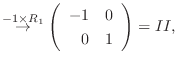 |
||
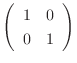 |
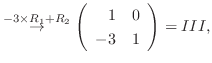 |
||
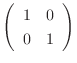 |
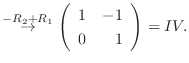 |
 と基本行列の積で表すには, 行列
と基本行列の積で表すには, 行列  に基本行列
に基本行列 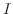 ,
, 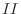 ,
, 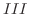 ,
, 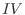 を左から順にかければよい.よって,
を左から順にかければよい.よって,
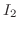 |
 |
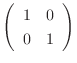 |
|
 |
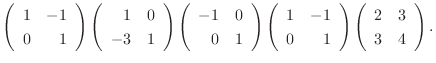 |
4.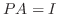 を満たす行列の積
を満たす行列の積 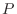 は次のようにして求めることができる.
は次のようにして求めることができる.
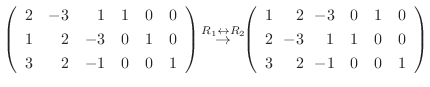 |
|||
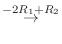 |
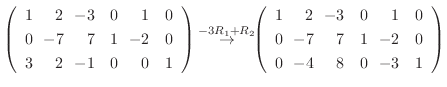 |
||
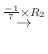 |
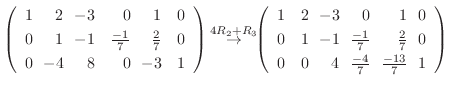 |
||
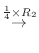 |
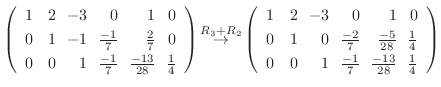 |
||
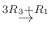 |
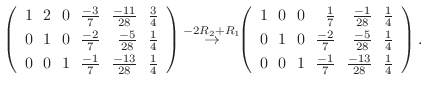 |
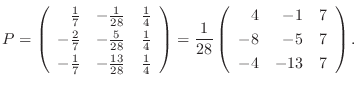
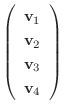
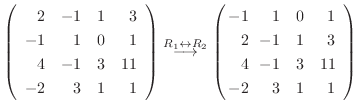
5.線形代数学入門定理より行空間の次元はその行列の階数と等しいので,
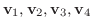 を行ベクトルとする行列の階数を求めればよい.
を行ベクトルとする行列の階数を求めればよい.
 |
 |
 |
|
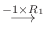 |
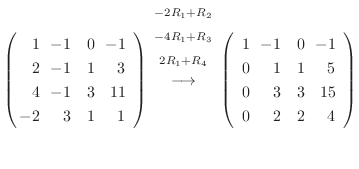 |
||
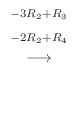 |
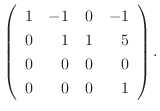 |
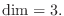
1.
![$\displaystyle [A: {\bf b}]$](img536.png) |
 |
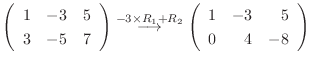 |
|
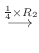 |
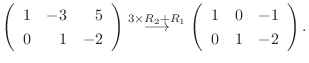 |
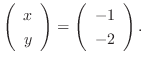
![$\displaystyle [A: {\bf b}]$](img536.png) |
 |
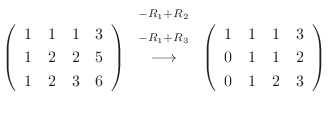 |
|
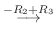 |
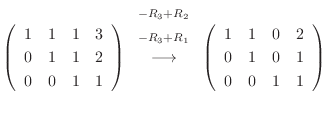 |
||
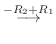 |
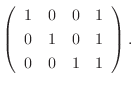 |
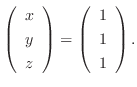
![$\displaystyle [A: {\bf b}]$](img536.png) |
 |
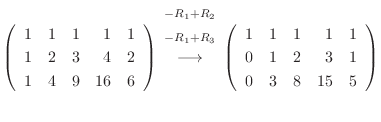 |
|
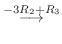 |
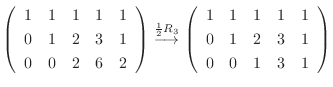 |
||
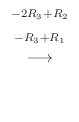 |
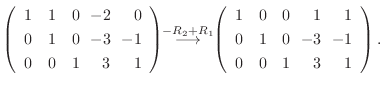 |
![${\rm rank}(A) = {\rm rank}([A: {\bf b}])$](img552.png) なので方程式は解をもつ.また
なので方程式は解をもつ.また
![$[A: {\bf b}]_{R}$](img553.png) を方程式に書き直すと
を方程式に書き直すと
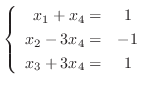
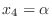 とおくと,
とおくと,
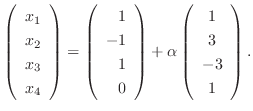
![$\displaystyle [A: {\bf b}]$](img536.png) |
 |
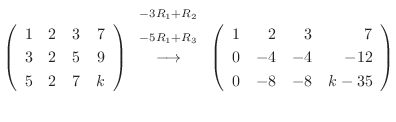 |
|
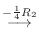 |
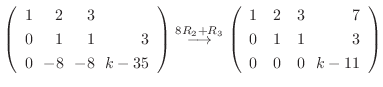 |
||
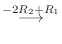 |
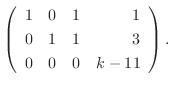 |
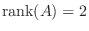 より
より
![${\rm rank}([A: {\bf b}])$](img564.png) も2でなければならない.言い換えると
も2でなければならない.言い換えると 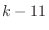 が0でなければこの連立方程式は解をもたない.よって
が0でなければこの連立方程式は解をもたない.よって 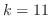 .さらに
.さらに 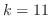 のとき,
のとき,
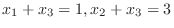 であるから,
であるから,
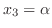 とおくと
とおくと
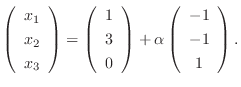
3.
Aが 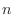 次の正則行列
次の正則行列
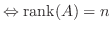
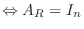 .
.
 |
 |
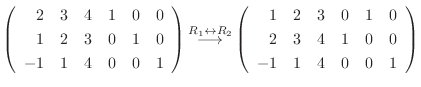 |
|
 |
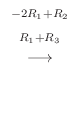 |
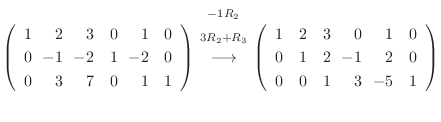 |
|
 |
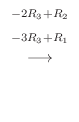 |
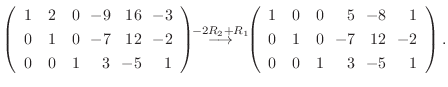 |
 は正則で
は正則で
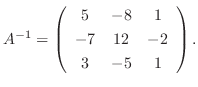
![$\displaystyle [A:I]$](img579.png) |
 |
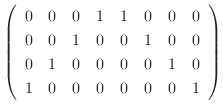 |
|
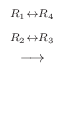 |
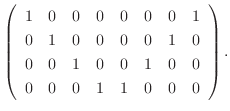 |
 は正則で
は正則で
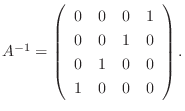
4. は
は 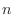 次の正則行列
次の正則行列
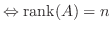 .よってこの場合
.よってこの場合
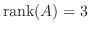 となるように
となるように 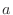 を定めればよい.
を定めればよい.
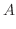 |
 |
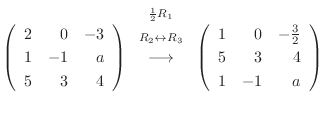 |
|
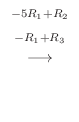 |
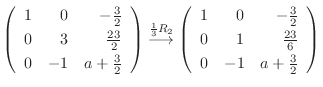 |
||
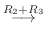 |
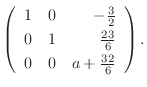 |
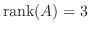 となるには
となるには
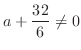 とならなければならない.よって
とならなければならない.よって
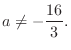
5. を基本行列の積で表すには, 単位行列から始めて基本変形を繰り返しながら
を基本行列の積で表すには, 単位行列から始めて基本変形を繰り返しながら  を作る.このとき用いた基本変形から生まれる基本行列を単位行列に左側から順にかけていけば, 基本行列の積で
を作る.このとき用いた基本変形から生まれる基本行列を単位行列に左側から順にかけていけば, 基本行列の積で  を表せる.
を表せる.
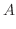 |
 |
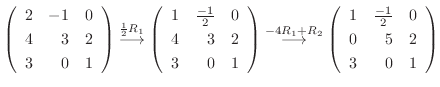 |
|
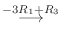 |
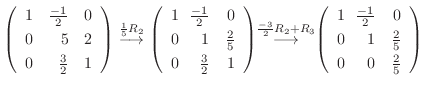 |
||
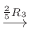 |
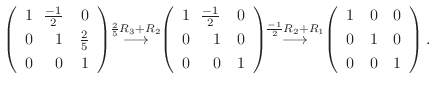 |
 は正則行列.次に, いま行なった基本変形を逆に戻し, その基本変形から生まれる基本行列を順にかけていくと
は正則行列.次に, いま行なった基本変形を逆に戻し, その基本変形から生まれる基本行列を順にかけていくと
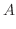 |
 |
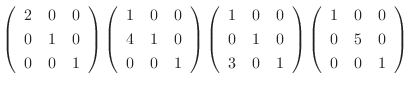 |
|
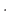 |
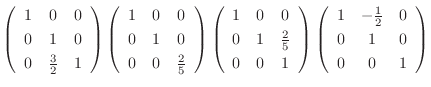 |
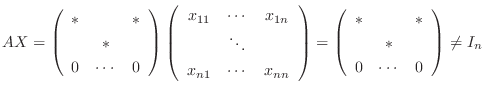
 は正則でない.
は正則でない.
別解
 を
を 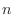 次の正方行列とする.
次の正方行列とする. のひとつの行の成分がすべて0ならば,
のひとつの行の成分がすべて0ならば,
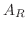 の少なくともひとつの行の成分はすべて0である.
よって
の少なくともひとつの行の成分はすべて0である.
よって
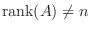 となり線形代数学入門定理3.3より
となり線形代数学入門定理3.3より  は正則でない.
は正則でない.
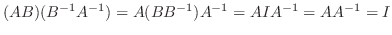
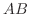 は正則.また
は正則.また
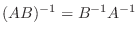 となる.
となる.
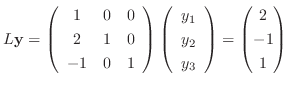
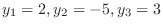 . したがって,
. したがって,
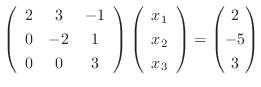
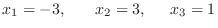
Gaussの消去法より
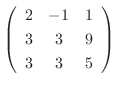 |
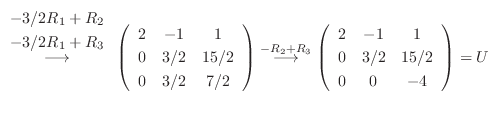 |
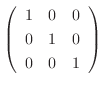 |
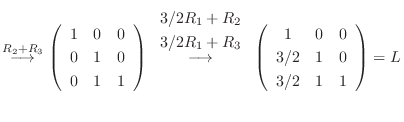 |
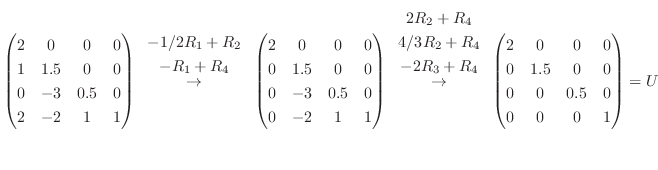
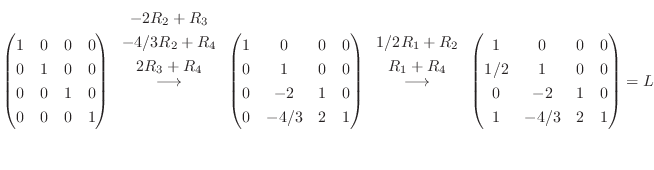
1.
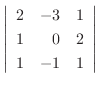 |
 |
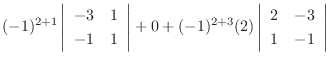 |
|
 |
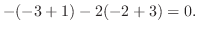 |
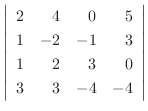
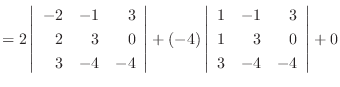
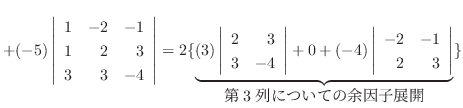
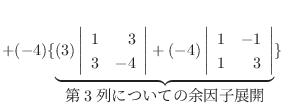
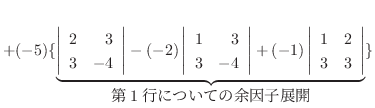
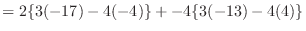
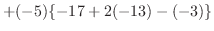
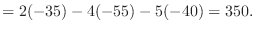
 |
 |
||
 |
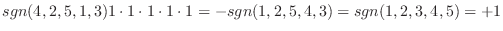 |
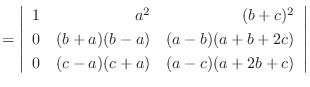
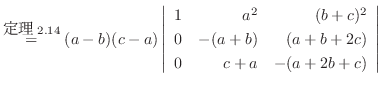
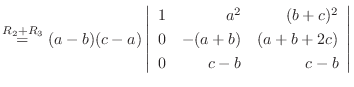
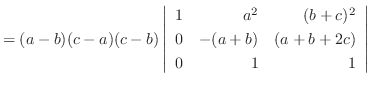
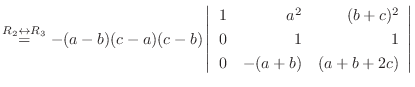
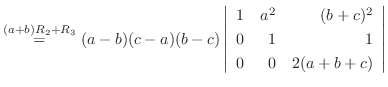
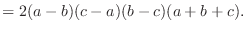
列を用いた因数分解を行なう.
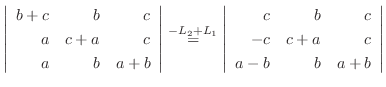 |
|||
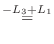 |
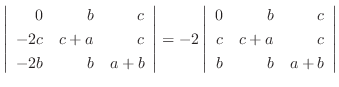 |
||
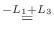 |
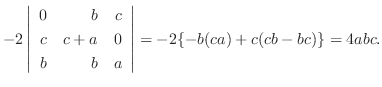 |
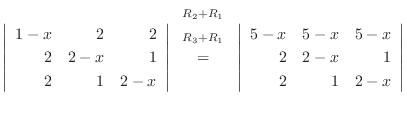 |
|||
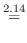 |
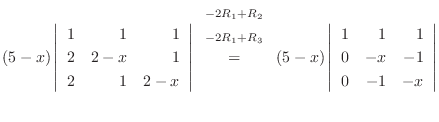 |
||
 |
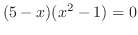 |
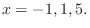
つまり
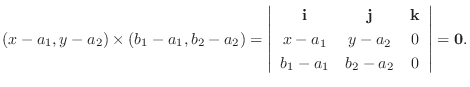
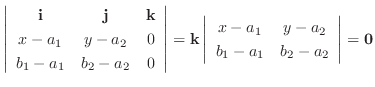
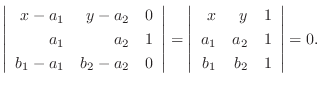
5.法線ベクトル
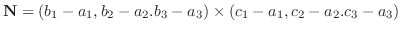 と平面上のベクトル
と平面上のベクトル
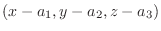 は直交するのでその内積は0.よってスカラー3重積
は直交するのでその内積は0.よってスカラー3重積
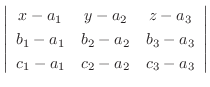 |
 |
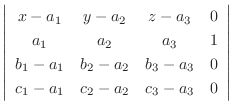 |
|
 |
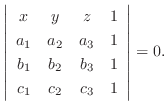 |
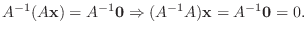
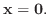
7.
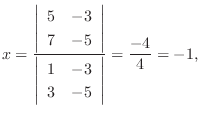
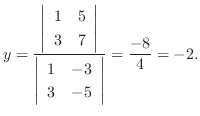
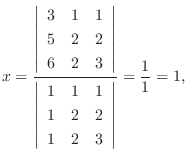
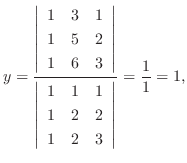
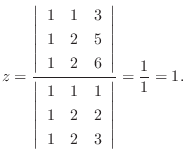
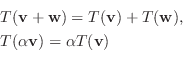
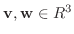 とすると,
とすると,
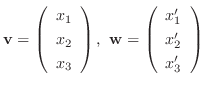 と表せる.ここで
と表せる.ここで
![$\displaystyle T_{1}[\left(\begin{array}{c}
x_{1}\\
x_{2}\\
x_{3}
\end{array}\...
...rray}{c}
x_{1}^{\prime}\\
x_{2}^{\prime}\\
x_{3}^{\prime}
\end{array}\right)]$](img671.png) |
 |
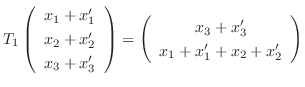 |
|
 |
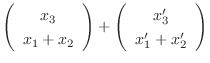 |
||
 |
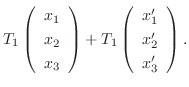 |
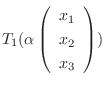 |
 |
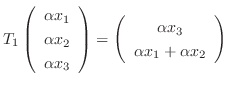 |
|
 |
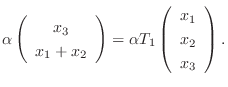 |
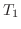 は線形写像.
は線形写像.
次に 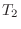 について調べる.
について調べる.
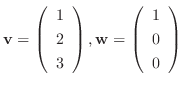 とおくと
とおくと
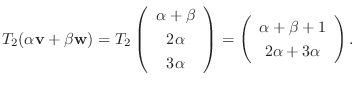
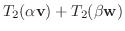 |
 |
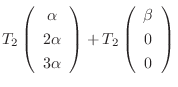 |
|
 |
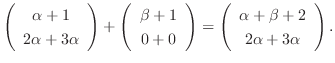 |
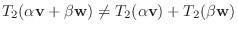 となるので
となるので 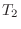 は線形写像ではない.
は線形写像ではない.
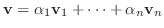
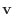 の
の 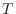 による像
による像
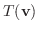 は
は 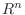 の元になるので
の元になるので
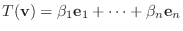
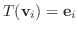 より
より
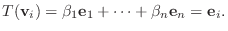
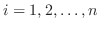 において
において
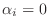 ならば
ならば
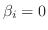 .また
.また
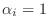 ならば
ならば
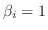 となるので
となるので
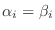 となる.よって
となる.よって
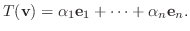
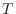 が線形写像であることを示す.
が線形写像であることを示す.
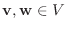 とすると,
とすると,
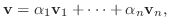
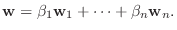
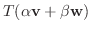 |
 |
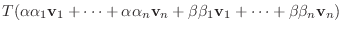 |
|
 |
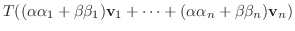 |
||
 |
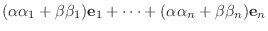 |
||
 |
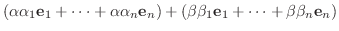 |
||
 |
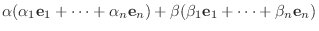 |
||
 |
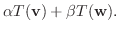 |
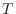 は線形写像となる.
は線形写像となる.
3.
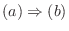
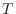 が同型写像なら線形代数学入門定理3.3より同型写像
が同型写像なら線形代数学入門定理3.3より同型写像
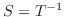 が存在し,
が存在し,
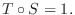
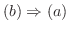
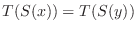 とおくと
とおくと
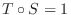 より
より
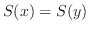 となるので
となるので 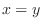 .また
.また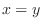 より
より
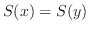 .よって
.よって 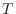 は単射.次に
は単射.次に 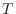 が 全射であることを示す.
が 全射であることを示す.
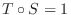 より
より
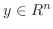 に対して
に対して
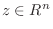 が存在し
が存在し
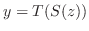 .また
.また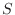 は
は 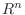 から
から 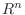 への写像よりある
への写像よりある
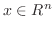 に対して
に対して 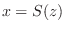 .よって
.よって 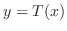 .
.
4.
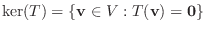 より
より
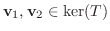 とすると,
とすると,
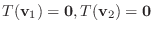 となる.よって任意の実数
となる.よって任意の実数
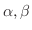 に対して,
に対して,
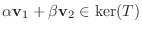 が成り立つことを示せばよい.つまり,
が成り立つことを示せばよい.つまり,
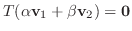 を示せばよい.さて,
を示せばよい.さて,
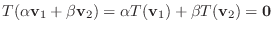
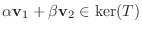 となり,
となり, 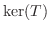 は部分空間である.
は部分空間である.
次に
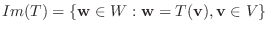 より
より
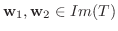 とすると,
とすると,
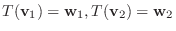 となる.よって任意の実数
となる.よって任意の実数
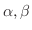 に対して,
に対して,
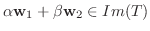 となることを示せばよい.つまり
となることを示せばよい.つまり
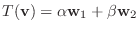 となるような
となるような
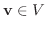 が存在することを示せばよい.さて,
が存在することを示せばよい.さて, 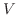 はベクトル空間なので,
はベクトル空間なので,
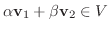 .また
.また
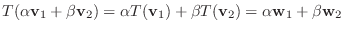
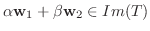 となり,
となり, 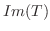 は部分空間である.
は部分空間である.
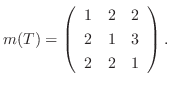
 が成り立ち,
が成り立ち,
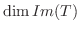 =
=
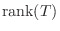 より,
より,
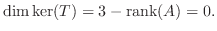
標準基底
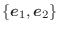 がどこに移るかを調べればよい.そこで,
がどこに移るかを調べればよい.そこで,
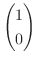 と
と
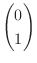 を
を
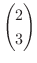 と
と
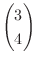 を用いて表すと,
を用いて表すと,
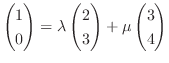
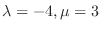 .同様に,
.同様に,
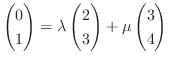
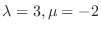 となる.
これより,
となる.
これより,
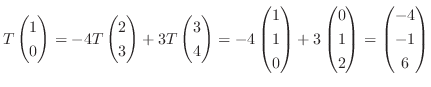
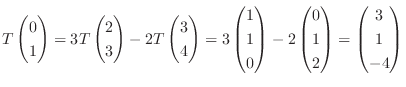
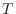 の行列表現は,
の行列表現は,
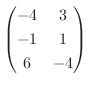 .
.
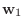 |
 |
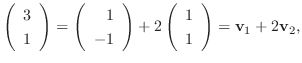 |
|
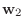 |
 |
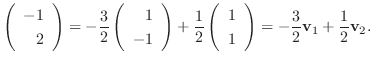 |
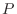 は
は
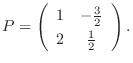
2.
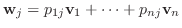 とおくと
とおくと
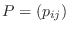 は
は
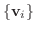 から
から
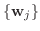 への変換行列.また
への変換行列.また
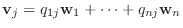 とおくと
とおくと
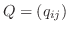 は
は
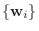 から
から
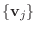 への変換行列で
への変換行列で
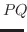 |
 |
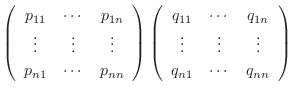 |
|
 |
 |
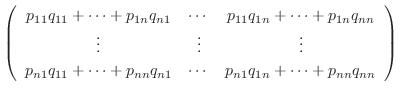 |
|
 |
 |
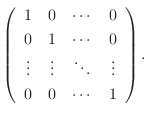 |
3.
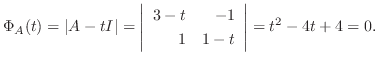
 の固有値は
の固有値は
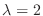 である.
である.
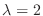 に対する固有ベクトルは
に対する固有ベクトルは
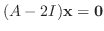 を満たす0でない
を満たす0でない
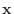 なので, 連立方程式を解くと
なので, 連立方程式を解くと
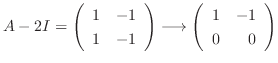
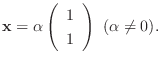
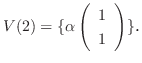
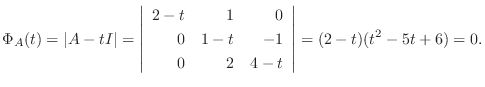
 の固有値は
の固有値は
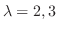 である.
である.
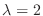 に対する固有ベクトルは
に対する固有ベクトルは
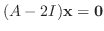 を満たす0でない
を満たす0でない
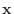 なので, 連立方程式を解くと
なので, 連立方程式を解くと

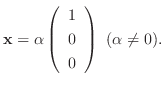
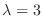 に対する固有ベクトルは
に対する固有ベクトルは
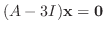 を満たす0でない
を満たす0でない
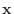 なので, 連立方程式を解くと
なので, 連立方程式を解くと
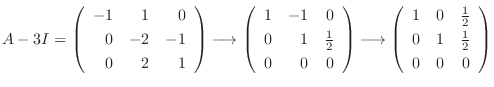
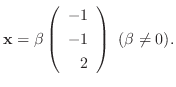
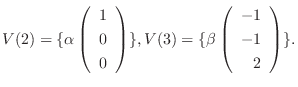
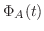 |
 |
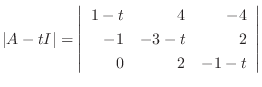 |
|
 |
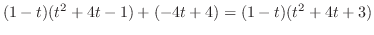 |
||
 |
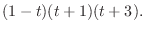 |
 の固有値は
の固有値は
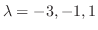 である.
である.
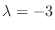 に対する固有ベクトルは
に対する固有ベクトルは
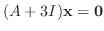 を満たす0でない
を満たす0でない
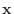 なので, 連立方程式を解くと
なので, 連立方程式を解くと
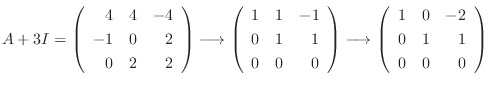
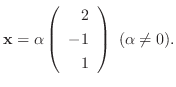
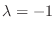 に対する固有ベクトルは
に対する固有ベクトルは
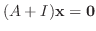 を満たす0でない
を満たす0でない
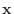 なので, 連立方程式を解くと
なので, 連立方程式を解くと
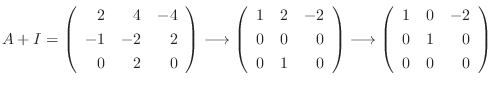
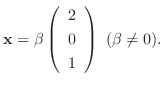
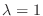 に対する固有ベクトルは
に対する固有ベクトルは
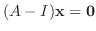 を満たす0でない
を満たす0でない
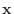 なので, 連立方程式を解くと
なので, 連立方程式を解くと
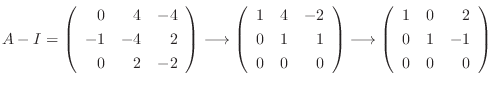
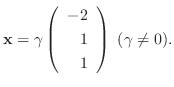
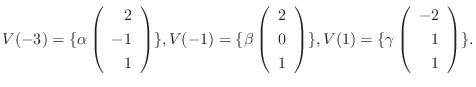
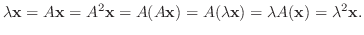
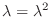 が成り立ち, これより
が成り立ち, これより
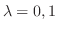 となる.
となる.
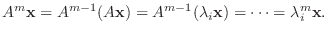
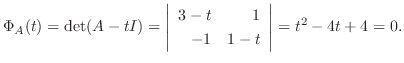
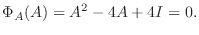
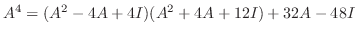 と表せるので,
と表せるので,
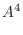 |
 |
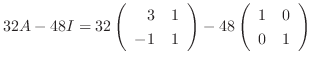 |
|
 |
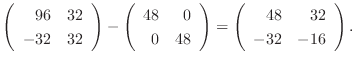 |
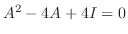 より
より
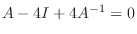 .よって
.よって
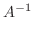 |
 |
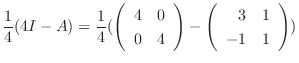 |
|
 |
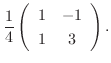 |
7.まず,
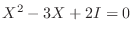 より
より
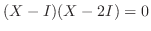 .よって
.よって 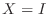 または
または 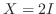 はこの2次方程式を満たす.次に
はこの2次方程式を満たす.次に
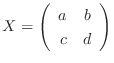 とすると, ケイリー・ハミルトンの定理より
とすると, ケイリー・ハミルトンの定理より
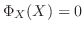 となるので,
固有方程式が
となるので,
固有方程式が
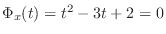 となる
となる 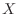 を求める.
を求める.
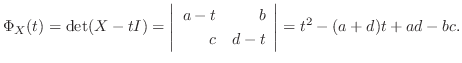
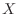 は
は
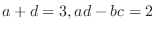 を満たせばよい.
を満たせばよい.
1.
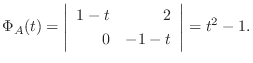
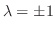 .
.
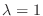 に対する固有ベクトルは
に対する固有ベクトルは
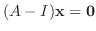 を満たす0でない
を満たす0でない
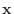 なので, 連立方程式を解くと
なので, 連立方程式を解くと
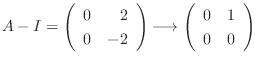
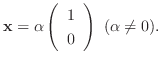
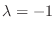 に対する固有ベクトルは
に対する固有ベクトルは
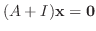 を満たす0でない
を満たす0でない
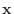 なので, 連立方程式を解くと
なので, 連立方程式を解くと
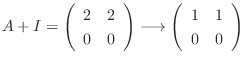
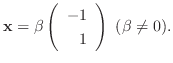
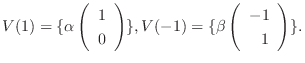
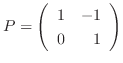 のとき,
のとき,
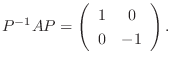
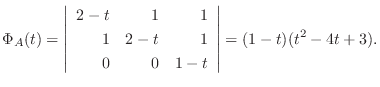
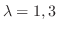 .
.
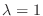 に対する固有ベクトルは
に対する固有ベクトルは
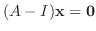 を満たす0でない
を満たす0でない
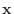 なので, 連立方程式を解くと
なので, 連立方程式を解くと
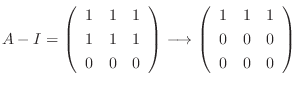
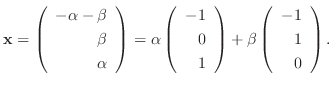
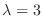 に対する固有ベクトルは
に対する固有ベクトルは
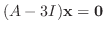 を満たす0でない
を満たす0でない
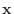 なので, 連立方程式を解くと
なので, 連立方程式を解くと
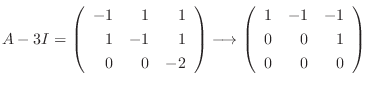
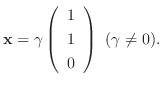
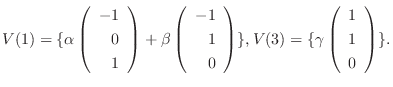
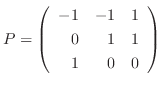 のとき,
のとき,
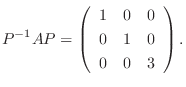
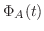 |
 |
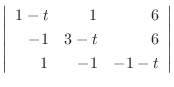 |
|
 |
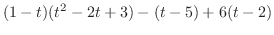 |
||
 |
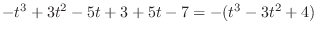 |
||
 |
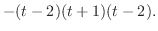 |
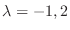 .
.
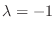 に対する固有ベクトルは
に対する固有ベクトルは
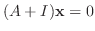 を満たす0でない
を満たす0でない
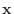 なので, 連立方程式を解くと
なので, 連立方程式を解くと
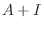 |
 |
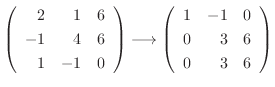 |
|
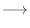 |
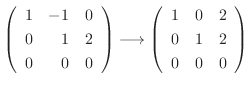 |
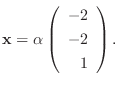
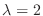 に対する固有ベクトルは
に対する固有ベクトルは
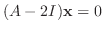 を満たす0でない
を満たす0でない
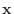 なので, 連立方程式を解くと
なので, 連立方程式を解くと
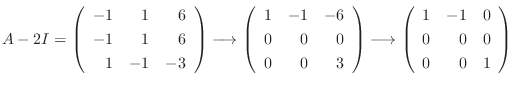
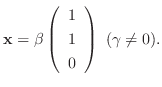
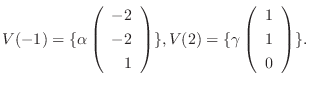

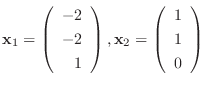
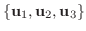 を作ると,
を作ると,
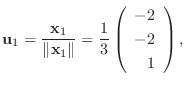
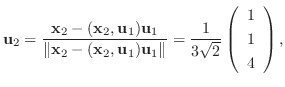
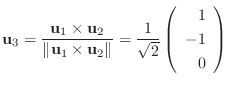
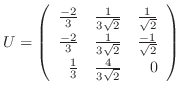 とおくと,
とおくと, 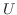 はユニタリ行列で
はユニタリ行列で
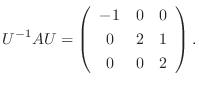
2.まず, 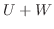 が直和ならば,
が直和ならば,
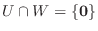 を示す.
を示す.
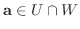 とおくと,
とおくと,
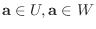 .よって
.よって
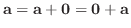 と表せる.しかし
と表せる.しかし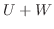 が直和なので, その表し方は一意的である.よって
が直和なので, その表し方は一意的である.よって
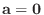 でなければならない.よって
でなければならない.よって
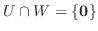 .また逆に
.また逆に
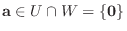 と仮定し,
と仮定し,
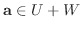 が
が
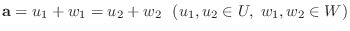
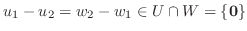
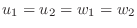 となり, 上のような表し方は一通りなので
となり, 上のような表し方は一通りなので 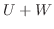 は直和である.
は直和である.
3.線形代数学入門定理次元公式より
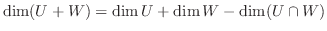 .また
.また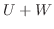 が直和ならば,
が直和ならば,
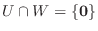 となり,
となり,
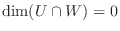 .よって
.よって
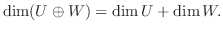
4.まず, 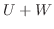 は直和であることを示す.演習問題4.1より
は直和であることを示す.演習問題4.1より
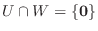 を示せばよい.
を示せばよい.
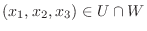 とおくと,
とおくと,
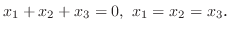
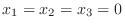 となり,
となり,
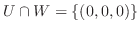 .
.
次に,
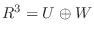 を示す.まず,
を示す.まず,
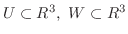 より,
より,
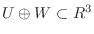 . また
. また
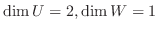 より,
より,
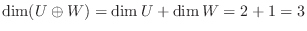
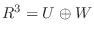 .
.
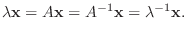
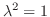 .
.
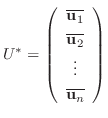
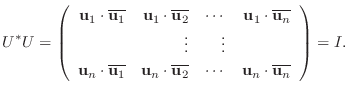
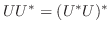 より,
より,
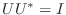 .
.
1.
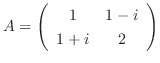 とおくと,
とおくと,
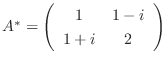 より,
より,
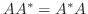 .よって
.よって  はユニタリ行列により対角化可能である.
はユニタリ行列により対角化可能である.
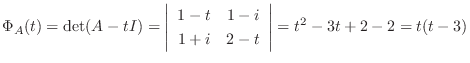
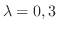 である.
である.
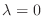 に対する固有空間は
に対する固有空間は
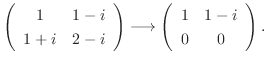
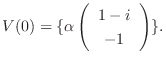
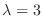 に対する固有空間は
に対する固有空間は
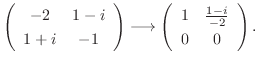
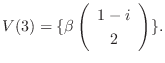
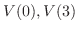 のそれぞれの正規直交基底として
のそれぞれの正規直交基底として
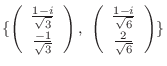
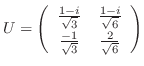
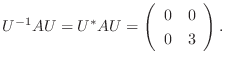
2.
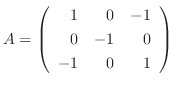 より
より  は実対称行列.よって線形代数学入門定理4.6より直交行列で対角化可能である.
は実対称行列.よって線形代数学入門定理4.6より直交行列で対角化可能である.
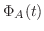 |
 |
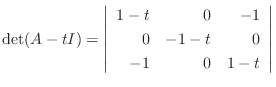 |
|
 |
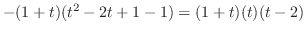 |
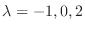 である.
である.
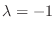 に対する固有空間は
に対する固有空間は
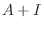 |
 |
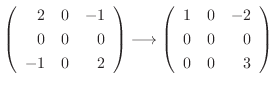 |
|
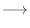 |
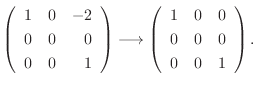 |
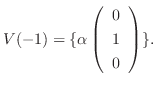
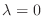 に対する固有空間は
に対する固有空間は
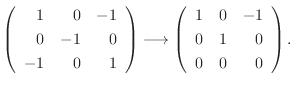
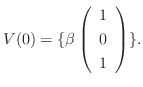
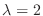 に対する固有空間は
に対する固有空間は
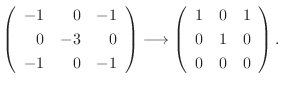
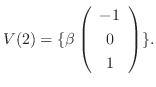
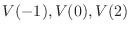 のそれぞれの正規直交基底として
のそれぞれの正規直交基底として
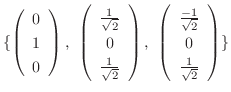
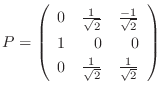
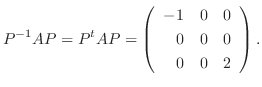
3.
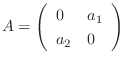 がユニタリ行列により対角行列に変換されるための必要十分条件は, 線形代数学入門定理4.5より
がユニタリ行列により対角行列に変換されるための必要十分条件は, 線形代数学入門定理4.5より  が正規行列.つまり
が正規行列.つまり
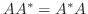 である.
である.
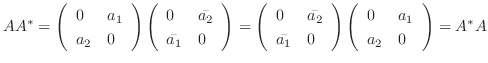
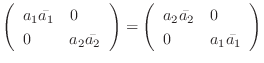
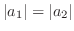 .
.
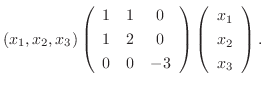
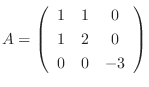 は実対称行列.よって線形代数学入門定理4.6より直交行列で対角化可能.
は実対称行列.よって線形代数学入門定理4.6より直交行列で対角化可能.
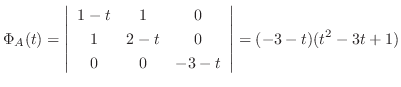
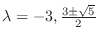 .よって
.よって
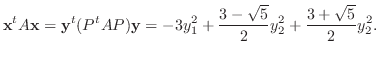
5.
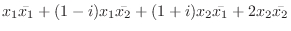 を行列を用いて表すと
を行列を用いて表すと
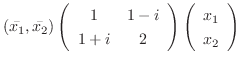
 はエルミート行列なので, 線形代数学入門定理4.5よりユニタリ行列による直交化が可能である.
はエルミート行列なので, 線形代数学入門定理4.5よりユニタリ行列による直交化が可能である.
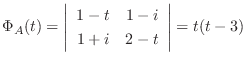
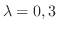 .よって
.よって
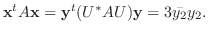
1. (a)