Next: 正規行列 Up: 行列の対角化 Previous: 行列の対角化 目次 索引
1. 次の行列は対角化可能か.可能ならば適当な正則行列 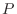 を求めて対角化せよ.もし不可能ならば三角化を行なえ.
を求めて対角化せよ.もし不可能ならば三角化を行なえ.
2. 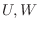 がベクトル空間
がベクトル空間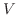 の部分空間であるとき,
の部分空間であるとき, 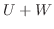 が直和であるための必要十分条件は
が直和であるための必要十分条件は
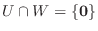 であることを証明せよ.
であることを証明せよ.
3. 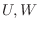 が有限次元のとき,
が有限次元のとき,
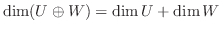
4. 3次元ベクトル空間
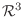 において
において
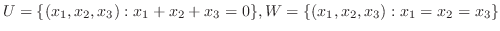
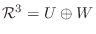 であることを証明せよ.
であることを証明せよ.
5. 直交行列の固有値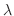 の絶対値はつねに
の絶対値はつねに 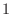 であることを証明せよ.
であることを証明せよ.
6. 正方行列 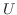 の列ベクトルが正規直交基底をなすとき,
の列ベクトルが正規直交基底をなすとき, 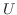 はユニタリ行列であることを証明せよ.
はユニタリ行列であることを証明せよ.