Next: 1次独立と1次従属 Up: ベクトル空間 Previous: 幾何ベクトルとベクトル空間 目次 索引
1.
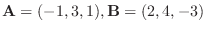 について, 次の値を求めよ.
について, 次の値を求めよ.
(a)
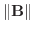 (b)
(b)
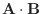 (c) A とB のなす角
(d) A方向の単位ベクトル
(c) A とB のなす角
(d) A方向の単位ベクトル
2. 次の集合のうち直交系はどれか.また直交系は対応する正規直交系を求めよ.
3. 点 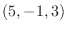 を通り, 法ベクトルが2i + j - kである平面の方程式を求めよ.
を通り, 法ベクトルが2i + j - kである平面の方程式を求めよ.
4. A,Bを空間のベクトルとするとき, 次の不等式を証明せよ.
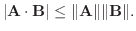
5. A, B, Cを空間のベクトルとするとき, 次の不等式を証明せよ.
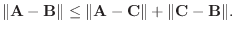
6. 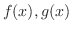 を
を ![$PC[a,b]$](img25.png) の関数とするとき, 次の不等式を証明せよ.
の関数とするとき, 次の不等式を証明せよ.
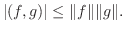
7. ![$PC[0,2]$](img27.png) において, 次の関数のノームを求めよ.
において, 次の関数のノームを求めよ.
8. 次にあげる3個の多項式はLegendreの多項式とよばれるものです.
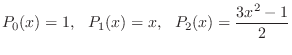
![$PC[-1,1]$](img32.png) で直交系をなすことを示せ.
で直交系をなすことを示せ.