Next: 部分空間と次元 Up: ベクトル空間 Previous: 内積空間 目次 索引
 外積
外積

ふたつのベクトルの外積を考えるために幾何ベクトルに戻ります.外積の定義は内積ほど簡単ではありませんが応用数学には欠かせないものです.ここでは外積の応用を3次元空間に限ります.他の空間には外積のやさしい一般化がないのです.
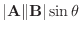 と等しく, 方向は, A,B の両方に垂直で, Aを
と等しく, 方向は, A,B の両方に垂直で, Aを
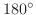 以内回転してB の方向に重ねるとき右ねじの進む方向として定まるベクトルを, A,B の 外積(cross product) といい
以内回転してB の方向に重ねるとき右ねじの進む方向として定まるベクトルを, A,B の 外積(cross product) といい
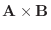 で表す.
で表す.
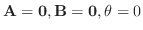 のとき, A とB に垂直な方向が定まらないが,
のとき, A とB に垂直な方向が定まらないが,
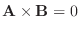 と定義する.
と定義する.
3次元空間では
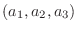 と
と
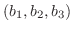 の外積は次の式で定義される.
の外積は次の式で定義される.
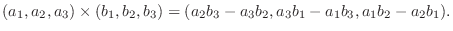
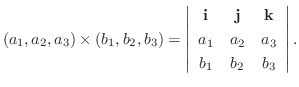
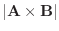 を内積を用いて表そう.
を内積を用いて表そう.
解
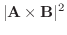 |
 |
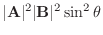 |
|
 |
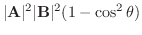 |
||
 |
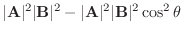 |
||
 |
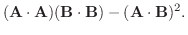 |
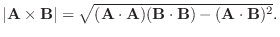

力学で点 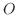 のまわりの力F の モーメント(moment)
のまわりの力F の モーメント(moment)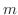 は,
は, 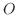 から力F の作用線までの距離を
から力F の作用線までの距離を 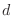 とするとき,
とするとき,
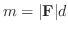 で与えられます.rを力の作用線上の任意の点
で与えられます.rを力の作用線上の任意の点  と
と 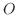 を結ぶベクトルだとすると,
を結ぶベクトルだとすると,
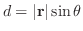 .よって
.よって
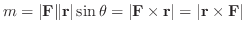
このとき,
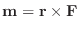 を点
を点 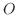 のまわりの力F の モーメントベクトル(moment vector) といいます.
のまわりの力F の モーメントベクトル(moment vector) といいます.
ある軸のまわりの剛体の回転は, 次のようにして, 角速度ベクトル(angular velocity)
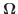 により一意的に表せます.ここで角速度ベクトル
により一意的に表せます.ここで角速度ベクトル
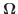 とは剛体を右ねじが回転する方向に回すとき, ねじの進む方向が
とは剛体を右ねじが回転する方向に回すとき, ねじの進む方向が
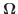 であり,
であり,
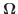 の大きさが回転の角速度となるベクトルのことです.剛体内の点
の大きさが回転の角速度となるベクトルのことです.剛体内の点  の速度ベクトル v は, 回転軸上の任意の点と
の速度ベクトル v は, 回転軸上の任意の点と  を結ぶベクトルを r とすると, 次の式で表せます.
を結ぶベクトルを r とすると, 次の式で表せます.
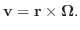
3つのベクトル A,B,C に対して,
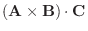 は実数となるのでスカラー三重積(scalar triple product) といい,
は実数となるのでスカラー三重積(scalar triple product) といい,
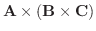 はベクトルになるので, ベクトル三重積(vector triple product) といいます.
はベクトルになるので, ベクトル三重積(vector triple product) といいます.
ベクトル三重積
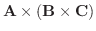 は B とC が作る平面上のベクトルです.よって, B とC が平行でなければ,
は B とC が作る平面上のベクトルです.よって, B とC が平行でなければ,
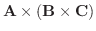 は次の式で表されます.
は次の式で表されます.
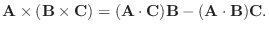
 1次結合
1次結合

ベクトル空間では和とスカラー倍は基本です.和はふたつのベクトル間の演算ですが, ベクトル空間では結合法則が成り立つので, 3つ, 4つとベクトルを加えることができます.このようにして作ったものをベクトルの1次結合といいます.
 のベクトル
のベクトル
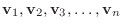 と実数
と実数
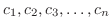 に対して,
に対して,
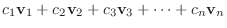
ここで注意しておきたいことは, ベクトル空間 のどんなベクトルによる1次結合も, また
のどんなベクトルによる1次結合も, また のベクトルになるということです.
のベクトルになるということです.
次に, 連続関数
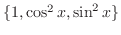 の1次結合をいくつか考えてみましょう.
の1次結合をいくつか考えてみましょう.
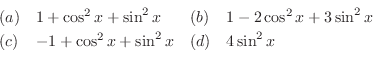
1次結合はすべての 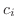 が0のとき, 0ベクトルになりますがその他のときも, 0ベクトルになることがあるでしょうか.上の例
が0のとき, 0ベクトルになりますがその他のときも, 0ベクトルになることがあるでしょうか.上の例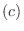 を見て下さい.
を見て下さい.
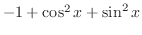 は0です.このように, 0でない
は0です.このように, 0でない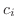 を使って作った1次結合が0と等しくなるとき, ベクトルの組
を使って作った1次結合が0と等しくなるとき, ベクトルの組
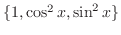 は1次従属であるといいます.
またそういう
は1次従属であるといいます.
またそういう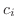 が存在しないとき, ベクトルの組は1次独立であるといいます.
が存在しないとき, ベクトルの組は1次独立であるといいます.
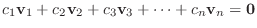
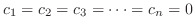 がいえれば,
がいえれば,
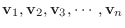 は 1次独立(linearly independent)であるといい, それ以外のとき,
は 1次独立(linearly independent)であるといい, それ以外のとき,
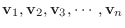 は 1次従属(linearly dependent)であるという.
は 1次従属(linearly dependent)であるという.
 は1次独立であることを証明しよう.
は1次独立であることを証明しよう.
解
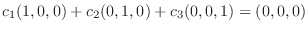 より
より
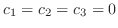 となるので,
となるので,
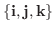 は1次独立である.
は1次独立である.

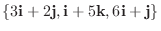 は1次独立であることを証明しよう.
は1次独立であることを証明しよう.
解
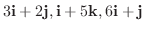 の1次結合は
の1次結合は
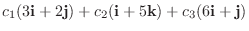 .これを書き直して0 とおくと,
.これを書き直して0 とおくと,
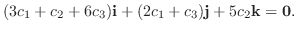
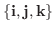 は1次独立なので,
は1次独立なので,
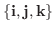 の係数はすべて0.つまり
の係数はすべて0.つまり
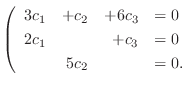
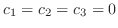 である.したがってこのベクトルは1次独立である.
である.したがってこのベクトルは1次独立である.

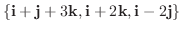 は1次従属か1次独立か調べよう.
は1次従属か1次独立か調べよう.
解
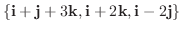 の1次結合を 0 とおくと,
の1次結合を 0 とおくと,
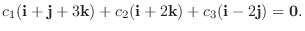
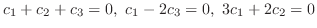
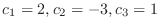 のように0以外の解をもっている.よって,
のように0以外の解をもっている.よって,
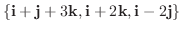 は1次従属である.
は1次従属である.

上の例題をもう少し注意深くみると,
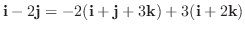 と表せることがかわります.一般に次のことがいえます.
と表せることがかわります.一般に次のことがいえます.
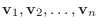 の1次結合で表されるならば,
w と
の1次結合で表されるならば,
w と
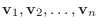 は互いに1次従属である.
は互いに1次従属である.
逆に, 数個のベクトルが互いに1次従属ならば, そのうちの 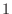 個は残りのベクトルの1次結合で表される.
個は残りのベクトルの1次結合で表される.
証明
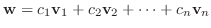
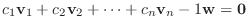
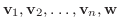 は互いに1次従属である.
は互いに1次従属である.
逆に,
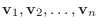 が1次従属ならば, 関係式
が1次従属ならば, 関係式
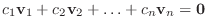
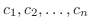 のうちには0でないものが少なくとも一つはある.そのうちの一つを
のうちには0でないものが少なくとも一つはある.そのうちの一つを
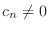 とすれば
とすれば
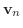 は
は
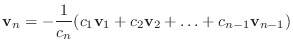
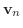 は
は
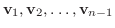 の1次結合で表される.
の1次結合で表される.

幾何ベクトルが1次独立かでないかを調べるとき, スカラー三重積を使うと簡単に調べられます.つまり
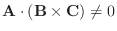 である.
である.
証明
演習問題1.3よりスカラー三重積は平行六面体の体積と考えられる.したがって,
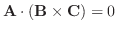 は A,B,C が同一平面上にあることと同値である.また, 定理1.1よりこれは A,B,C が1次従属であるのと同値である.
は A,B,C が同一平面上にあることと同値である.また, 定理1.1よりこれは A,B,C が1次従属であるのと同値である.

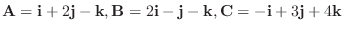 は1次独立であることを証明しよう.
は1次独立であることを証明しよう.
解
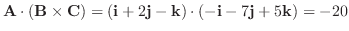 .よって1次独立である.
.よって1次独立である.

1.
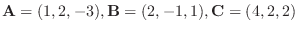 について,
について,
2. 点(1,0,1)を通り,
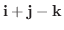 と
と
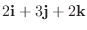 によって作られる平面に平行な平面を求めよ.
によって作られる平面に平行な平面を求めよ.
3. 2点
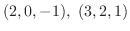 を通り平面
を通り平面
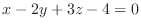 に垂直な平面の方程式を求めよ.
に垂直な平面の方程式を求めよ.
4.
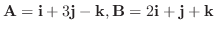 を2辺とする三角形の面積を求めよ.
を2辺とする三角形の面積を求めよ.
5.
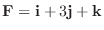 のとき, 点
のとき, 点 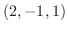 のまわりの力F のモーメントベクトルを求めよ.
のまわりの力F のモーメントベクトルを求めよ.
6. 剛体が直線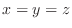 のまわりを角速度ベクトル
のまわりを角速度ベクトル
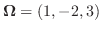 で回転しているとき, 剛体内の点
で回転しているとき, 剛体内の点 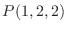 の速度を求めよ.
の速度を求めよ.
7. 3つのベクトル A,B,C の作る平行六面体の体積は, スカラー三重積
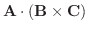
8.
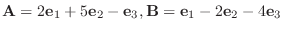 で
で
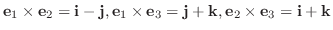 のとき,
のとき,
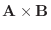 を求めよ.
を求めよ.
9.
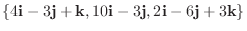 は1次独立か1次従属か調べよ.
は1次独立か1次従属か調べよ.
10. 次の関数はどの区間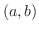 でも1次独立であることを示せ.
でも1次独立であることを示せ.
11. 幾何ベクトル A, B が1次独立であるための必要十分条件は
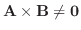 であることを示せ.
であることを示せ.