Next: 1次独立と1次従属 Up: ベクトル空間 Previous: 幾何ベクトルとベクトル空間 目次 索引
 区分的に連続な関数
区分的に連続な関数

ここでは幾何ベクトル空間には似ても似つかないベクトル空間を紹介します.まず区間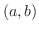 で連続な関数の集まりを
で連続な関数の集まりを 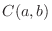 で表し, 区間
で表し, 区間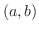 で区分的に連続な関数(piecewise continuous function) の集まりを
で区分的に連続な関数(piecewise continuous function) の集まりを 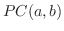 で表します. 関数
で表します. 関数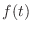 が区間
が区間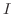 で区分的に連続とは、
で区分的に連続とは、
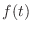 は区間
は区間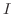 で有限個の点を除いて連続である.
で有限個の点を除いて連続である.
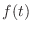 の不連続点
の不連続点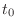 では, 左側および右側極限値が存在する.
では, 左側および右側極限値が存在する.
ここで、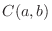 と
と 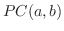 の
の 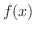 と
と 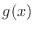 に対して, 和およびスカラー倍を次のように定義します.
に対して, 和およびスカラー倍を次のように定義します.
1.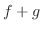 は点
は点 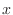 で
で 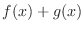 の値をとる関数.
の値をとる関数.
2.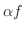 は点
は点 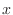 で
で
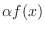 の値をとる関数.
の値をとる関数.
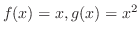 のとき,
のとき,
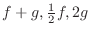 を求めよう.
を求めよう.
解
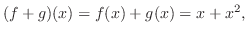
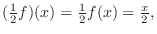
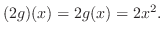

この和とスカラー倍によって, ベクトル空間になるための9個の性質が
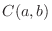 と
と 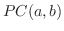 において成り立ちます.
において成り立ちます.
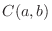 と
と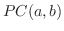 はベクトル空間をなす.
はベクトル空間をなす.
これより, ベクトル空間に含まれる 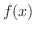 や
や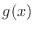 をベクトルとよぶことができます.幾何ベクトルと姿や形が違いますが立派なベクトルです.ベクトル空間の中には大きさや方向を考える必要のないものもありますが, 大きさを与えることのできるベクトル空間を 計量ベクトル空間(normed vector space) といいます.ここでは内積が定義できる計量ベクトル空間について考えます.
をベクトルとよぶことができます.幾何ベクトルと姿や形が違いますが立派なベクトルです.ベクトル空間の中には大きさや方向を考える必要のないものもありますが, 大きさを与えることのできるベクトル空間を 計量ベクトル空間(normed vector space) といいます.ここでは内積が定義できる計量ベクトル空間について考えます.
 内積
内積

幾何ベクトルにおいて次の3つのことは基本です.(1)和, (2)スカラー倍, (3)内積(スカラー積).
和とスカラー倍については、すでに学んだので、ここでは幾何ベクトルの内積について紹介します.
0でないベクトルA, Bとそれらのなす角を
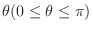 とします.このとき, 実数
とします.このとき, 実数
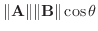 をAとBの内積(dot product)またはスカラー積といい
をAとBの内積(dot product)またはスカラー積といい
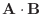 と表します.つまり
と表します.つまり
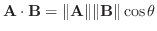
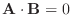 と定めます.
と定めます.
これまでに私たちは和およびスカラー倍の一般化を行いました.そこでここでは内積の一般化に挑戦します.
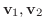 に対して, 実数
に対して, 実数
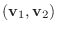 または
または
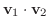 が定まり, 次の性質をもつとき,
が定まり, 次の性質をもつとき,
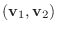 または
または
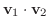 を
を
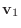 と
と
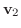 の 内積(inner product) という.
の 内積(inner product) という.
あるベクトル空間のすべてのベクトル
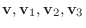 とすべての実数
とすべての実数
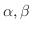 に対して,
に対して,
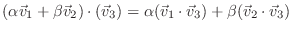 (線形性)
(線形性)
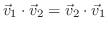 対称性
対称性
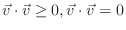 と
と
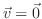 は同値.
は同値.
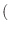 正定値性
正定値性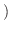 が成り立つ.
が成り立つ.
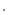 B は次のように与えられます.
B は次のように与えられます.
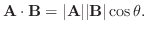
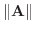 と
と 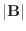 は A とB の長さを表し,
は A とB の長さを表し, 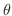 はベクトル A とB が作る小さいほうの角度を表します.このスカラー積は内積の性質
はベクトル A とB が作る小さいほうの角度を表します.このスカラー積は内積の性質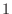 から
から 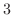 を満たしていることを示してみよう.
を満たしていることを示してみよう.
解
A とB のなす角を 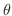 , A とA+B のなす角を
, A とA+B のなす角を 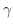 ,A とC のなす角を
,A とC のなす角を 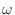 とすると,
とすると,
1.
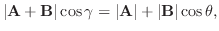
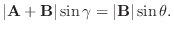
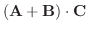 |
 |
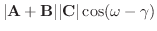 |
|
 |
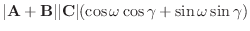 |
||
 |
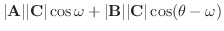 |
||
 |
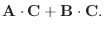 |
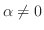 のとき,
のとき,
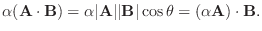
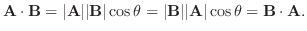
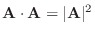 , よって,
, よって,
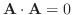 とA = 0は同値.
とA = 0は同値.

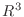 に内積を定義してみよう.
に内積を定義してみよう.
解
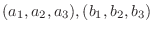 を
を 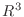 の任意の元とすると,
の任意の元とすると,
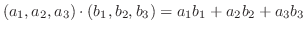
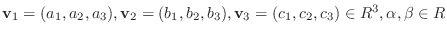 とすると
とすると
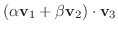 |
 |
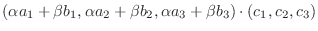 |
|
 |
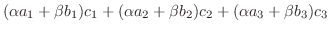 |
||
 |
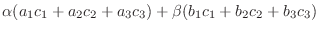 |
||
 |
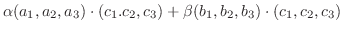 |
||
 |
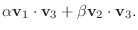 |
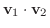 |
 |
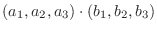 |
|
 |
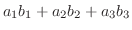 |
||
 |
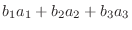 |
||
 |
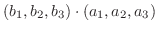 |
||
 |
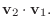 |
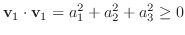
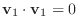 |
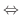 |
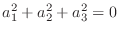 |
|
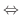 |
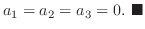 |
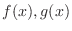 を
を ![$PC[a,b]$](img145.png) の元とすると, 内積
の元とすると, 内積 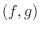 は次の式で与えられる.
は次の式で与えられる.
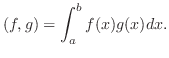
 を満たしています.
を満たしています.
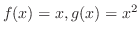 が
が ![$PC[0,2]$](img149.png) に属しているとき, 内積
に属しているとき, 内積 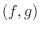 を計算しよう.
を計算しよう.
解
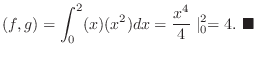
ベクトル空間上に内積が定義されると, ノーム(ベクトルの大きさ)が定義されます.
 ノーム(norm) は
ノーム(norm) は
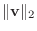 で表され, 次の式で与えられる.
で表され, 次の式で与えられる.
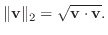
よって、内積の性質より、 ノームは次の性質を持っている.
ノームは次の性質を持っている.
すべてのベクトル
 とすべての実数
とすべての実数  に対して,
に対して,
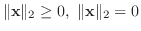 と
と
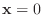 は同値
は同値
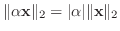
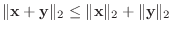
例えば、幾何ベクトル空間では,
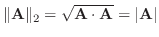 となるのでA の長さと同じです.3次元ベクトル空間では
となるのでA の長さと同じです.3次元ベクトル空間では
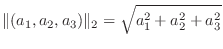
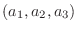 までの最短距離と考えられます. 関数空間 (function space)
までの最短距離と考えられます. 関数空間 (function space) ![$PC[a,b]$](img145.png) では,
では,
![$\displaystyle \Vert f\Vert _{2} = \{\int_{a}^{b}[f(x)]^2dx\}^{1/2}.$](img161.png)
この ノームの他にも、
ノームの他にも、
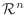 でよく用いられるものに、
でよく用いられるものに、
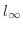 ノームがあります.
ノームがあります.
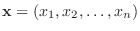 の
の
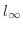 ノーム(norm) は
ノーム(norm) は
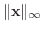 で表され, 次の式で与えられる.
で表され, 次の式で与えられる.
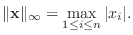
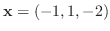 の
の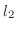 ノームと
ノームと
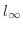 ノームを求めよう.
ノームを求めよう.
解
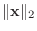 |
 |
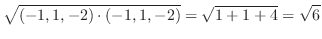 |
|
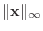 |
 |
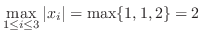 |
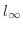 ノームも
ノームも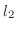 ノームと同様に次の性質を持っています.
ノームと同様に次の性質を持っています.
すべてのベクトル
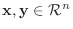 とすべての実数
とすべての実数  に対して,
に対して,
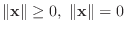 と
と
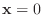 は同値
は同値
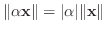
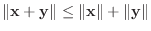
 直交
直交

2つの幾何ベクトルが直交すると、
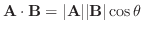 で
で
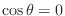 となるので、内積は零.また、
となるので、内積は零.また、
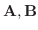 が零ベクトルでなく、内積が零ならば、
が零ベクトルでなく、内積が零ならば、
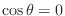 となり、
となり、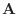 と
と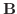 は直交していることが分かります.
は直交していることが分かります.
このように、ベクトル空間に内積が定義されると, ノームだけでなく垂直という概念の一般化として直交を定義できます.
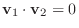 のとき, ベクトル
のとき, ベクトル
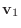 とベクトル
とベクトル
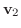 は 直交(orthogonal)しているという.また異なるベクトルがみな直交しているベクトルの集合を 直交系(orthogonal system) という.
は 直交(orthogonal)しているという.また異なるベクトルがみな直交しているベクトルの集合を 直交系(orthogonal system) という.
幾何ベクトル空間では, 有向線分A,B の内積
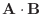 は例題
1.2より
は例題
1.2より
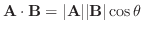 で与えられるので, もし0でない有向線分A,B に対して, 内積
で与えられるので, もし0でない有向線分A,B に対して, 内積
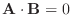 ならば
ならば
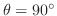 .つまり, A とB は垂直となります.
.つまり, A とB は垂直となります.
3次元ベクトル空間でベクトル
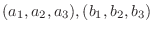 の内積は例題1.2より,
の内積は例題1.2より,
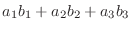 , また3次元ベクトルを幾何ベクトルと考えると,
, また3次元ベクトルを幾何ベクトルと考えると,
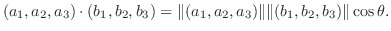
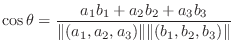
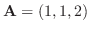 と
と
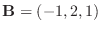 のなす角を求めよう.
のなす角を求めよう.
解
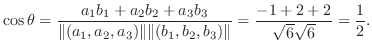
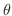 を
を
![$\displaystyle{[0, \frac{\pi}{2}]}$](img188.png) で捜すと
で捜すと
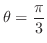 となる.
となる.

 平面の方程式
平面の方程式

空間の中に直交座標系を取り, 平面を考えます.平面とはある点を通り, その法ベクトルが一定な面と考えることができます.ここで, 法ベクトル(normal vector) とは, 面に接するベクトルに直交するベクトルのことです.内積を使うと簡単にこの平面の方程式が求まります.まず点
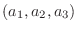 を求める平面上の点とします.そしてN =
を求める平面上の点とします.そしてN = 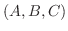 をその平面の法ベクトルとします.
をその平面の法ベクトルとします.
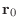 を原点と点
を原点と点
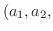
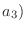 を結ぶ位置ベクトル, rを原点と点
を結ぶ位置ベクトル, rを原点と点
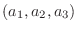 以外の平面上の点を結ぶ位置ベクトルとします.すると
以外の平面上の点を結ぶ位置ベクトルとします.すると
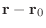 は平面上のベクトルとなるので,
は平面上のベクトルとなるので,
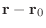 とN の間の角は
とN の間の角は
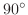 .よって
.よって
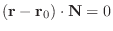 となり, これが求める平面の方程式です.
となり, これが求める平面の方程式です.
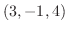 を通り, 法ベクトル
を通り, 法ベクトル 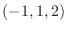 をもつ平面の方程式を求めよう.
をもつ平面の方程式を求めよう.
解
位置ベクトル rを(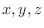 )とすると, 平面の方程式は
)とすると, 平面の方程式は
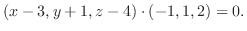
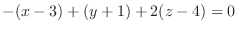
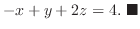
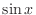 と
と 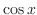 は
は
![$[-\pi,\pi]$](img204.png) で直交するが
で直交するが
![$\displaystyle{[0,\frac{\pi}{4}]}$](img205.png) では直交しないことを示そう.
では直交しないことを示そう.
解
![$[-\pi,\pi]$](img204.png) で
で
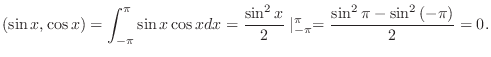
![$\displaystyle{[0,\frac{\pi}{4}]}$](img205.png) で
で
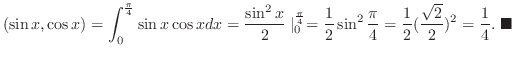
関数空間での直交は直角に交わるということではありませんので注意して下さい.
0でない幾何ベクトル Aをその大きさで割り, 単位ベクトル
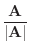 を求めることがよくあります.もっと一般的な場合にもベクトル vをそのノームで割り, 単位ベクトル
を求めることがよくあります.もっと一般的な場合にもベクトル vをそのノームで割り, 単位ベクトル
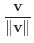 を求めることがあります.このようにして大きさが1のベクトルを求めることを, 正規化(normalize)するといいます.また, 直交系のすべてのベクトルを正規化してできた集合を 正規直交系(orthonormal system) といいます.正規直交系の例として3次元ベクトル空間での{i,j,k} があげられます.なぜこれが大事なのか次の節ではっきりするでしょう.
を求めることがあります.このようにして大きさが1のベクトルを求めることを, 正規化(normalize)するといいます.また, 直交系のすべてのベクトルを正規化してできた集合を 正規直交系(orthonormal system) といいます.正規直交系の例として3次元ベクトル空間での{i,j,k} があげられます.なぜこれが大事なのか次の節ではっきりするでしょう.
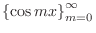 は
は ![$[0,\pi]$](img211.png) で直交系をなすことを示し, 対応する正規直交系を求めよう.
で直交系をなすことを示し, 対応する正規直交系を求めよう.
解
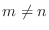 のとき,
のとき,
 |
 |
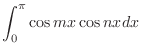 |
|
 |
![$\displaystyle \frac{1}{2}\int_{0}^{\pi}[\cos{(m+n)x} + \cos{(m-n)x}]dx$](img215.png) |
||
 |
![$\displaystyle \frac{1}{2}[\frac{\sin{(m+n)x}}{(m+n)} + \frac{\sin{(m-n)x}}{(m-n)}] \mid_{0}^{\pi} = 0.$](img216.png) |
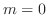 のとき,
のとき,
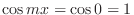 より
より
![$\displaystyle \Vert 1 \Vert = [ \int_{0}^{\pi}(1)^2 dx]^{1/2} = \sqrt{\pi}. $](img219.png)
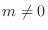 のとき,
のとき,
![$\displaystyle \Vert\cos{mx}\Vert = [ \int_{0}^{\pi}\cos^2{mx} dx]^{1/2} = \sqrt{\frac{\pi}{2}}. $](img221.png)
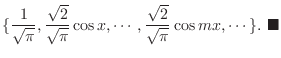
 フーリエ級数
フーリエ級数

この正規直交系を用いると, 区分的に連続な関数
![$f(x) \in [0,L]$](img223.png) は, 次の式で表現することができます.
は, 次の式で表現することができます.
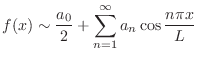
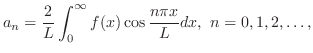
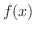 のフーリエ級数(Fourier series)といい,
のフーリエ級数(Fourier series)といい, 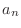 をフーリエ係数(Fourier coefficient)といいます.
をフーリエ係数(Fourier coefficient)といいます.
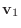 と
と
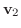 に対して, 三角不等式
に対して, 三角不等式
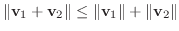
解
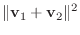 |
 |
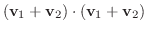 |
|
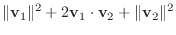 |
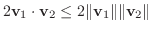
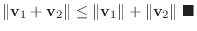
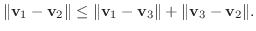
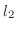 ノームは私たちが普段使っている距離とほぼ同じ働きをすることが分かります.
ノームは私たちが普段使っている距離とほぼ同じ働きをすることが分かります.
![$PC[0,2]$](img149.png) において,
において, 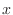 と
と 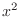 の距離を求めよう.
の距離を求めよう.
解
![$\displaystyle \Vert x - x^2\Vert = [\int_{0}^{2}(x -x^2)^2 dx]^{1/2} = \frac{4}{\sqrt{15}} .
\ensuremath{ \blacksquare}
$](img235.png)
1.
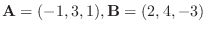 について, 次の値を求めよ.
について, 次の値を求めよ.
(a)
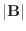 (b)
(b)
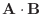 (c) A とB のなす角
(d) A方向の単位ベクトル
(c) A とB のなす角
(d) A方向の単位ベクトル
2. 次の集合のうち直交系はどれか.また直交系は対応する正規直交系を求めよ.
3. 点  を通り, 法ベクトルが2i + j - kである平面の方程式を求めよ.
を通り, 法ベクトルが2i + j - kである平面の方程式を求めよ.
4. A,Bを空間のベクトルとするとき, 次の不等式を証明せよ.
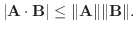
5. A, B, Cを空間のベクトルとするとき, 次の不等式を証明せよ.
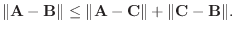
6. 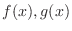 を
を ![$PC[a,b]$](img145.png) の関数とするとき, 次の不等式を証明せよ.
の関数とするとき, 次の不等式を証明せよ.
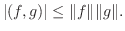
7. ![$PC[0,2]$](img149.png) において, 次の関数のノームを求めよ.
において, 次の関数のノームを求めよ.
8. 次にあげる3個の多項式はLegendreの多項式とよばれるものです.
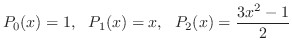
![$PC[-1,1]$](img248.png) で直交系をなすことを示せ.
で直交系をなすことを示せ.