Next: 内積空間 Up: ベクトル空間 Previous: ベクトル空間 目次 索引
平面や空間での有向線分によって表されるベクトルにはすでに出会ったことがあるでしょう.ここでは, 一般のベクトルと区別するため, 有向線分で表されるベクトルを 幾何ベクトル(geometric vector) とよびます.幾何ベクトルは, 方向と大きさをもつ線分を表します.方向と大きさはまだ定義していないので, この初等的な幾何ベクトルの定義は完全ではありません.ただ, 皆さんが日常使っているユークリッド幾何での方向と大きさと考えれば十分です.
これから先, 幾何ベクトルはいつも有向線分で表されます.幾何ベクトルは, 皆さんが今まで扱ってきた数と違い, 同じ方向と大きさをもちさえすれば等しいということができます.つまり, どの有向線分もそれに平行で大きさが同じ有向線分で置き換えても等しく, このことから, 有向線分は方向と大きさを変えないで自由に動かすことができます.
初めに, ふたつの初等的な演算, 加法(vector addition)およびスカラー乗法(scalar multiplication)を幾何ベクトルに対して定義します.ベクトルの和を作る操作を加法といい, ベクトルを定数倍することをスカラー乗法といいます.このふたつの演算とそこから派生する性質が, 後にもっと完全なベクトルの定義へと導いてくれます.そして, この定義は後の多くの応用のための基礎概念となってくれます.
 幾何ベクトルの和
幾何ベクトルの和

ふたつの 幾何ベクトルの和(vector sum) は, 一方の幾何ベクトルの尻尾(始点)をもう一方の幾何ベクトルの頭(終点)につけることにより定義されます.よって, ふたつの幾何ベクトルの和は最初の幾何ベクトルの尻尾から次の幾何ベクトルの頭を結んだ有向線分で表せます.ほかの見方をすると, ふたつの幾何ベクトル A,B の和A 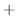 B は A とB によって作られる平行四辺形の対角線として表せます.
B は A とB によって作られる平行四辺形の対角線として表せます.
幾何ベクトルの和は次のような性質をもっています.各自確かめておいて下さい.
 幾何ベクトルのスカラー倍
幾何ベクトルのスカラー倍

幾何ベクトルの スカラー倍 (scalar multiple)  A は幾何ベクトル Aを実数
A は幾何ベクトル Aを実数  の大きさ
の大きさ 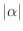 倍することで定義されます.ただし,
倍することで定義されます.ただし,  が負のときは方向が反対になります.幾何ベクトルのスカラー倍は次のような性質をもっています.各自確かめておいて下さい.
が負のときは方向が反対になります.幾何ベクトルのスカラー倍は次のような性質をもっています.各自確かめておいて下さい.
 と
と 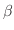 に対して,
に対して,  (
(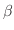 A) = (
A) = (
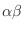 )A が成り立つ.(結合法則)
)A が成り立つ.(結合法則)
 と
と 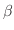 に対して, (
に対して, (
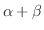 )A =
)A =  A +
A + 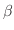 A が成り立ち, 任意の幾何ベクトル A とB に対して,
A が成り立ち, 任意の幾何ベクトル A とB に対して,  (A+B) =
(A+B) =  A +
A +  B が成り立つ.(分配法則)
B が成り立つ.(分配法則)
 0 = 0 が成り立つ.
0 = 0 が成り立つ.
 幾何ベクトル空間
幾何ベクトル空間

平面や空間の幾何ベクトルにおいて上の1から9までの性質が成り立ちます.このとき, 平面や空間の幾何ベクトルの集まりを 幾何ベクトル空間 (geometric vector space) といいます.幾何ベクトル空間はしばしばユークリッド空間ともよばれ, これから学ぶもっと抽象的なベクトル空間の一例です.一般に, 和およびスカラー倍が上の性質1から9を満たす物の集まりを ベクトル空間(vector space) とよび, その集合の要素を ベクトル(vector) といいます.よって, これから登場してくるベクトルには, 幾何ベクトルとは似ても似つかない物が沢山あります.
 空間のベクトル
空間のベクトル

平面上の幾何ベクトル
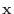 に対して、直交座標を用意し、始点が原点になるように平行移動したとき、終点の座標
に対して、直交座標を用意し、始点が原点になるように平行移動したとき、終点の座標
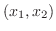 をこの幾何ベクトルとみなしてやります. つまり、
をこの幾何ベクトルとみなしてやります. つまり、
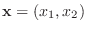 とします. すると、2つの幾何ベクトル
とします. すると、2つの幾何ベクトル
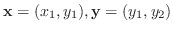 の和の
の和の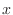 座標は、
座標は、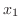 に
に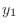 を加えた値になり、また、
を加えた値になり、また、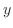 座標は
座標は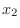 に
に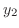 を加えた値になることが分かります. そこで、
を加えた値になることが分かります. そこで、
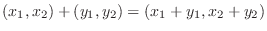
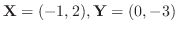 について,
について,
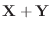 を求めよ.
を求めよ.
解
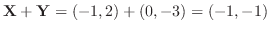

この考え方を一般化するため、3次元の空間の幾何ベクトルに直交座標を用意し、始点が原点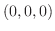 になるように平行移動したときの終点の座標を
になるように平行移動したときの終点の座標を
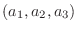 とします.
とします.
空間のベクトル(space vector) は3個の実数の組
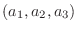 で表され,
で表され, 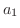 を
を 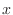 -成分,
-成分, 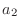 を
を 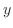 -成分,
-成分, 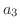 を
を 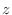 -成分といいます.これらのベクトルの集まりを{
-成分といいます.これらのベクトルの集まりを{
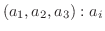 実数 } で表し, 加法およびスカラー乗法を適宜決めることにより, ベクトル空間にすることができます.このベクトル空間を 3次元ベクトル空間(three dimensional vector space) といい
実数 } で表し, 加法およびスカラー乗法を適宜決めることにより, ベクトル空間にすることができます.このベクトル空間を 3次元ベクトル空間(three dimensional vector space) といい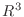 で表します.
で表します.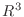 では, ベクトルの和は対応する成分どうしの和によって定義します.つまり
では, ベクトルの和は対応する成分どうしの和によって定義します.つまり
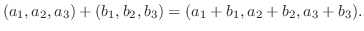
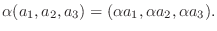
この空間の零元を 零ベクトル(zero vector) といい(0,0,0)で表します.3個の実数の組
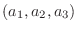 自身は方向も大きさももっていませんが,
自身は方向も大きさももっていませんが,
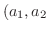 ,
, 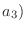 を直交座標上の点
を直交座標上の点
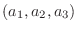 と考え, 原点からこの点にのびる有向線分を表すものとします.この考え方により幾何ベクトルと空間のベクトルを同じものとして扱うことができます.よって, ベクトルの大きさ
と考え, 原点からこの点にのびる有向線分を表すものとします.この考え方により幾何ベクトルと空間のベクトルを同じものとして扱うことができます.よって, ベクトルの大きさ
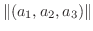 は, 原点と点
は, 原点と点
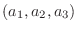 を結ぶ線分の距離となり,
を結ぶ線分の距離となり,
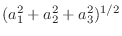 で表せます.
で表せます.
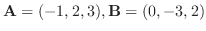 について, 次の値を求めよう.
について, 次の値を求めよう.
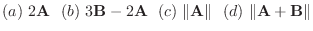
解
(a)
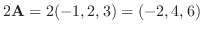 .
.
(b)
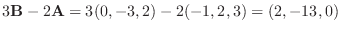 .
.
(c)
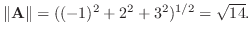
(d)
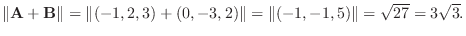

(1,0,0),(0,1,0),(0,0,1)という3つのベクトルはそれぞれi,j,kで表されます.この記号を使うと, ベクトル
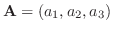 は
は
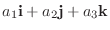 と表せます(どうやって?).またベクトル i,j,k のように大きさが1のベクトルを 単位ベクトル(unit vector) といいます.
と表せます(どうやって?).またベクトル i,j,k のように大きさが1のベクトルを 単位ベクトル(unit vector) といいます.
4個の実数の組, 5個の実数の組, または  個の実数の組(n-tuples)についても, 3個の組のときと同じ様に扱うことができます.ただ, 紙面の都合上, たとえば, 5個の実数の組は
個の実数の組(n-tuples)についても, 3個の組のときと同じ様に扱うことができます.ただ, 紙面の都合上, たとえば, 5個の実数の組は
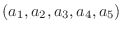 と表す代わりに,
と表す代わりに,
 と表すこともあります.その和およびスカラー倍は次のように定義します.
と表すこともあります.その和およびスカラー倍は次のように定義します.
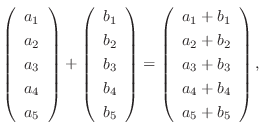
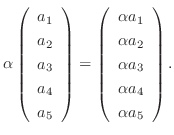
 個の実数の組についても和およびスカラー倍が定義できます.そしてこの和とスカラー倍はベクトル空間の性質1から9を満たします.
個の実数の組についても和およびスカラー倍が定義できます.そしてこの和とスカラー倍はベクトル空間の性質1から9を満たします.
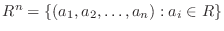 はベクトル空間をなす.
はベクトル空間をなす.
1. ベクトル A = 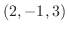 とベクトル B =
とベクトル B = 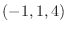 について, 次の値を求めよ.
について, 次の値を求めよ.
2. ベクトル A = 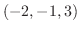 とベクトル B =
とベクトル B = 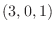 について, 次のベクトルを
について, 次のベクトルを
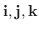 を用いて表せ.
を用いて表せ.
3. 1.1で定義した幾何ベクトルの和は性質1から5を満たすことを示せ.
4. 1.1で定義したスカラー倍は性質6から9を満たすことを示せ.
5. 1.1で定義した空間のベクトルの和およびスカラー倍は性質1から9を満たすことを示せ.
6. ベクトル A とB の始点が同じとき, A とB の作る角を二等分するベクトル Cを求めよ.
7.
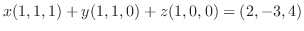 を解き,
を解き, 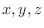 を求めよ.
を求めよ.