Next: Rotation Up: Scalar field, vector field Previous: Surface integrals Contents Index
 defined in an area of space.
The component of
defined in an area of space.
The component of
 is
is
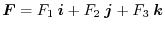
 is called the divergence of the vector field and defined as follows.
is called the divergence of the vector field and defined as follows.
|
If we use the operator  ,we can write div
,we can write div
 .
.
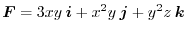 .
.
Answer
 |
 |
 |
|
 |
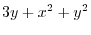 |
Next, let's think about what the divergence of a vector field is, using actual physical phenomena. Here, we consider the movement of liquid, gas, etc. spreading in space. At this time, the velocity of the particles in that space is a vector field and
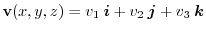 .Here, consider a Cartesian coordinate system with the point P in space as the origin, as shown in the figure
.Here, consider a Cartesian coordinate system with the point P in space as the origin, as shown in the figure ![[*]](crossref.png) .
Imagine a small rectangular parallelepiped
.
Imagine a small rectangular parallelepiped
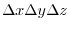 in a liquid.The area formed by
in a liquid.The area formed by
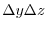 is denoted by
is denoted by
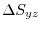 .
.
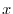 component of the vector perpendicular to the plane of the rectangular parallelepiped of the fluid entering the rectangular parallelepiped at the point
component of the vector perpendicular to the plane of the rectangular parallelepiped of the fluid entering the rectangular parallelepiped at the point 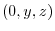 is
is
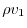 , where
, where 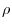 is the density of the liquid. Therefore, the flow rate of the fluid flowing from the back surface within the unit time
is the density of the liquid. Therefore, the flow rate of the fluid flowing from the back surface within the unit time 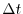 is
is
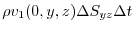
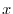 component of the vector perpendicular to the plane of the rectangular parallelepiped of the fluid coming out of the rectangular parallelepiped is
component of the vector perpendicular to the plane of the rectangular parallelepiped of the fluid coming out of the rectangular parallelepiped is
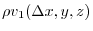 |
 |
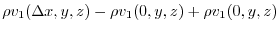 |
|
 |
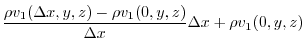 |
||
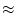 |
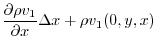 |
Therefore, the flow rate of the fluid flowing out from the front surface is
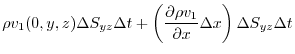
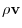 on six closed surfaces
on six closed surfaces
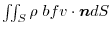 is , As learned in the previous chapter, it represents the total flow velocity (total flow rate), so it can be approximated by adding all of these.
is , As learned in the previous chapter, it represents the total flow velocity (total flow rate), so it can be approximated by adding all of these.
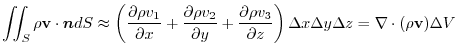
Here, the left side is the flow rate of the fluid flowing out from the surface  of a small rectangular parallelepiped to the outside in 1 second. In other words, it is considered to be the flow rate of the fluid that springs out in one second. Therefore
of a small rectangular parallelepiped to the outside in 1 second. In other words, it is considered to be the flow rate of the fluid that springs out in one second. Therefore
|
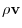 at P.Thus at P
at P.Thus at P
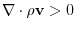 implies spill out. implies spill out. |
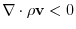 implies swallow. implies swallow. |
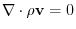 implies equilibrium. implies equilibrium. |
Basic formula
For every vector field
 ,
,
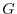 , and the scalar field
, and the scalar field  ,the following formula holds..
,the following formula holds..
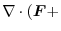
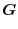
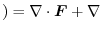
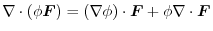
Proof
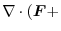 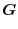  |
 |
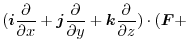   |
|
 |
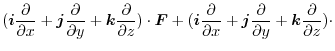  |
||
 |
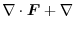 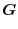 |
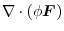 |
 |
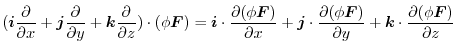 |
|
 |
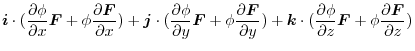 |
||
 |
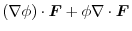 |
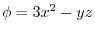 ,
,
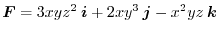 ,find the following scalar.
,find the following scalar.
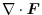 (2)
(2)
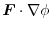 (3)
(3)
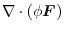 Answer (1)
Answer (1)
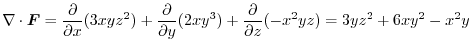
(2)
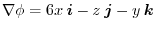 implies
implies
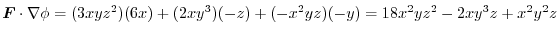
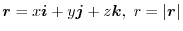 .Prove the following:
.Prove the following:
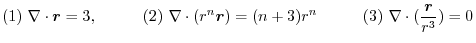
Answer (1)
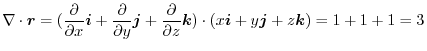
(2) By the differentiation of composite functions,,
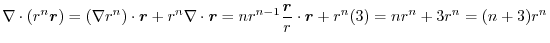
(3)
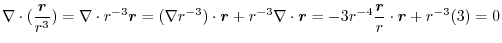
Laplacian
If
 is conservative, then
is conservative, then
 can be expressed by
can be expressed by
 |
 |
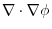 |
|
 |
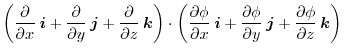 |
||
 |
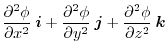 |
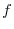 and denoted by
and denoted by
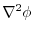 or
or
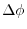 .Here,the inner product of the operators
.Here,the inner product of the operators
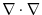 is represented by
is represented by 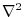 . Then
. Then
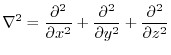
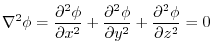
 is calledharmonic function
.
is calledharmonic function
.
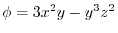 のとき,
のとき,
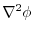 .
Answer
.
Answer
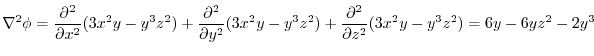
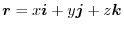 ,
,
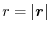 . Find the followings.
. Find the followings.
(1)
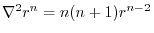
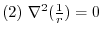
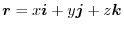 ,
,
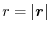 .
.
(1) Prove that
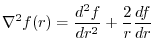 よ.
よ.
(2) Find 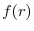 so that
so that
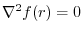 ..
..
Answer (1)
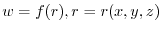 implies
implies
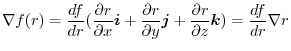
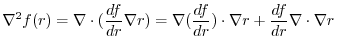
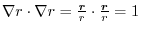 . Also,
. Also,
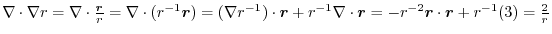 . Therefore,
. Therefore,
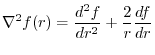
(2) Since
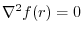 ,we have
,we have
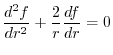
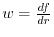 ,then
,then
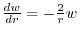 and it is separable.Thus,
and it is separable.Thus,
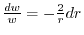 and integrate both sides, we have
and integrate both sides, we have
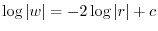 . Thus,
. Thus,
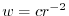 .
.
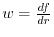 and
and
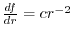 .Therefore,
.Therefore,
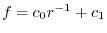 .
.
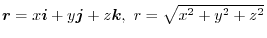 . Then
. Then
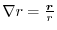
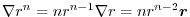
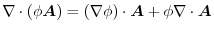
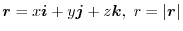 .Find the following scalar.
.Find the following scalar.
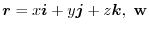 be a constant vector. Then show that .
be a constant vector. Then show that .
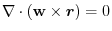
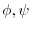 , prove the followings.
(1)
, prove the followings.
(1)
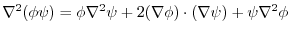
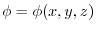 which satisfies
which satisfies
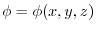
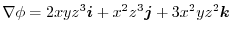 .provided
.provided
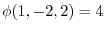 .
.
 , show the following.
, show the following.
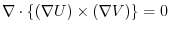
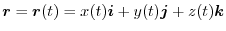 and the scalar field
and the scalar field
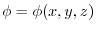 ,show that the derivative
,show that the derivative
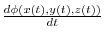 of
of  along the curve is equal to
along the curve is equal to
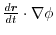 .
.
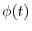 which is composed by putting
which is composed by putting
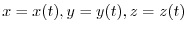 into
into
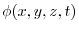 is
is
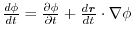 .provided,
.provided,
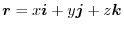 .
.