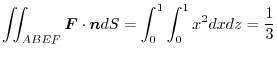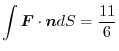Next: Divergence Up: Scalar field, vector field Previous: Line integral Contents Index
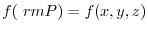 be the scalar field defined for any point
be the scalar field defined for any point
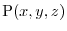 on the surface
on the surface
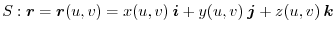 .Here,
.Here, is a smooth surface.
is a smooth surface.
Divide  into
into  small faces
small faces
 , and represent this division with
, and represent this division with  . Next, let the area of the curved surface
. Next, let the area of the curved surface 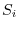 be
be
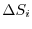 , and take the point
, and take the point
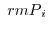 in
in 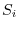 and consider the following sum.
and consider the following sum.
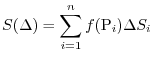
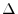 is made as small as possible, if
is made as small as possible, if 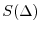 approaches
approaches  as much as possible, this limit value
as much as possible, this limit value  is called surface integral of the scalar field
is called surface integral of the scalar field 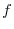 and denoted by
and denoted by
|
Here the area element 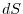 is approximated by the area of parallelogram with the sides
is approximated by the area of parallelogram with the sides
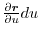 and
and
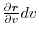 .
.
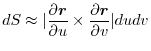
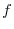 on the surface
on the surface  is expressed as follows.
is expressed as follows.
|
Here, 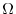 is the area on the
is the area on the 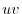 plane that corresponds to
plane that corresponds to  .
.
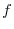 on the paraboloid
on the paraboloid
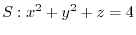 where
where  .
.
Answer
Let
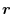 be the position vector corresponds to
be the position vector corresponds to
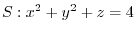 . Then
. Then
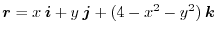
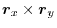 of
of  .
.
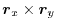 |
 |
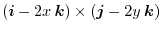 |
|
 |
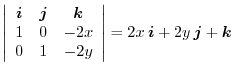 |
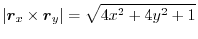
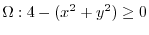 . Then
. Then
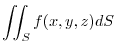 |
 |
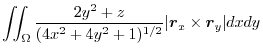 |
|
 |
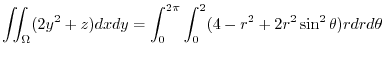 |
||
 |
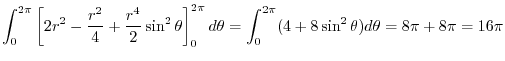 |
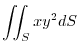 , where
, where
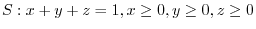 .
.
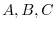 be the intersection of the plane
be the intersection of the plane
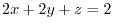 and
and 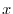 -axis,
-axis,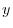 -axis,
-axis, 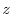 -axis and let the
-axis and let the  ABC be the surface
ABC be the surface  . Find
. Find
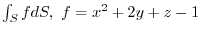 .
.
Surface integral of vector field
As in the line integral, we define surface integral of
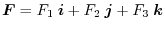 on the surface
on the surface  using the normal vector
using the normal vector
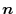 of
of  or area vector
or area vector 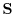 and expressed as
and expressed as
|
Note that the direction of
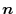 and the direction of
and the direction of
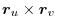 are the same.
are the same.
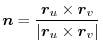
Therefore, the surface integral of the vector field
 on the surface
on the surface  is expressed by the double integral as follows.
is expressed by the double integral as follows.
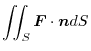 |
 |
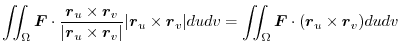 |
|
 |
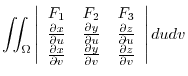 |
Also, using the directional cosine
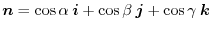 can be written as follows.
can be written as follows.
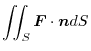 |
 |
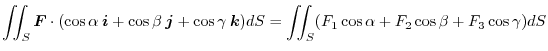 |
|
 |
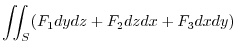 |
 be the surface represented by the equation
be the surface represented by the equation
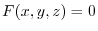 . Prove that the unit normal vector
. Prove that the unit normal vector
 of the surface
of the surface  is given by the following equation. Here
is given by the following equation. Here
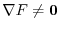 .
.
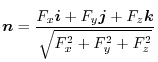
Flux
Here, when the vector field is the velocity field at a certain point when the fluid flows constantly in the flow tube,
is the velocity field at a certain point when the fluid flows constantly in the flow tube,
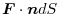 is called flux towards
is called flux towards
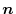 of
of
 .Therefore, the flux of
.Therefore, the flux of
 is
is 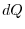 and the surface integral is
and the surface integral is
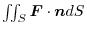 which is called flux integral and Reprresents the total flux (total flow rate).
which is called flux integral and Reprresents the total flux (total flow rate).
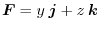 ,surface be
,surface be
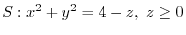 .Find the surface integral of
.Find the surface integral of
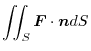
Answer
The position vector is
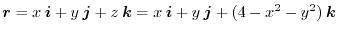 . Then
. Then
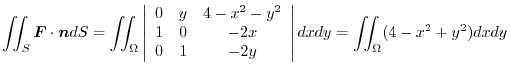
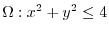 . Then
. Then
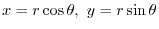 implies
implies
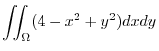 |
 |
![$\displaystyle \int_{0}^{2\pi} \int_{0}^{2}(4 - r^2 + 2r^2 \sin^{2}{\theta})r dr...
...eft[2r^2 - \frac{r^2}{4} + \frac{r^4}{2}\sin^{2}\theta \right ]_{0}^{2} d\theta$](img610.png) |
|
 |
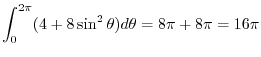 |
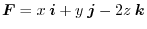 , and the surface be
, and the surface be
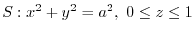 .Then find the surface integral of
.Then find the surface integral of
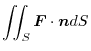 .
.
 be the sphere of the radius
be the sphere of the radius 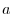 with the center O.Let
with the center O.Let
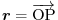 be the position vector of
be the position vector of 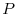 .Then by taking the unit normal vector
.Then by taking the unit normal vector
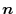 of the sperical surface
of the sperical surface  outward, prove the followings.
outward, prove the followings.
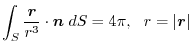
Answer Since
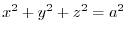 ,for
,for 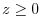 ,the position vector is
,the position vector is
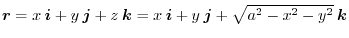 . Thus,
. Thus,
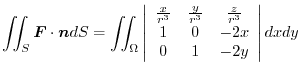
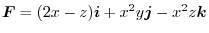 ,Let the surface
,Let the surface  be a bounded part of the plane
be a bounded part of the plane
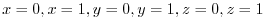 .Then find the surface integral
.Then find the surface integral
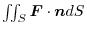 .
.
Answer
![\includegraphics[width = 6cm]{VECANALFIG/cube.eps}](img622.png)
For the plane DEFG: since 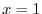 , the position vector is
, the position vector is
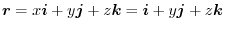 . Here the positive direction is from the bck of the plane to the front of DEFG. Thus, the unit normal vector is
. Here the positive direction is from the bck of the plane to the front of DEFG. Thus, the unit normal vector is
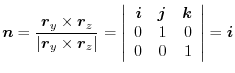
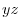 plane is
plane is
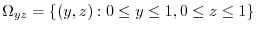 . Then,
. Then,
![$\displaystyle \iint_{DEFG}\boldsymbol{F}\cdot\boldsymbol{n}dS = \int_{0}^{1}\in...
...;dz = \int_{0}^{1}(2-z)dx = \left[2z - \frac{z^2}{2}\right]_{0}^1 = \frac{3}{2}$](img628.png)
For the plane ABCO: since 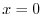 , the position vector is
, the position vector is
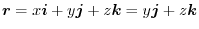 . Here,the positive direction is the direction of the back of plane ABCO to the front.Thus,the unit normal vector is
. Here,the positive direction is the direction of the back of plane ABCO to the front.Thus,the unit normal vector is
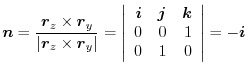
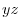 plane is
plane is
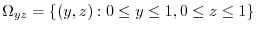 . Then
. Then
![$\displaystyle \iint_{ABCO}\boldsymbol{F}\cdot\boldsymbol{n}dS = \int_{0}^{1}\in...
...y=0}^{1}\;dz = \int_{0}^{1}zdx = \left[\frac{z^2}{2}\right]_{0}^1 = \frac{1}{2}$](img632.png)
For the plane ABEF: since 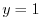 , the position vector is
, the position vector is
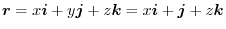 . Here the positive direction is the direction of the back of the plane ABEF to the front. Thus, the unit normla vector is
. Here the positive direction is the direction of the back of the plane ABEF to the front. Thus, the unit normla vector is
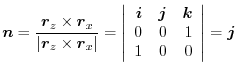
 plane is
plane is
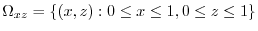 . Then
. Then