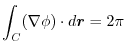Next: Surface integrals Up: Scalar field, vector field Previous: Gradient and directional derivative Contents Index
 the curve connecting two points R,Q. However, this curve should be a smooth curve. Let
the curve connecting two points R,Q. However, this curve should be a smooth curve. Let 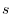 be the arc length measured along
be the arc length measured along  .Then, as we learned in Chapter 2, the points on the curve
.Then, as we learned in Chapter 2, the points on the curve  can be expressed by
can be expressed by 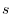 as a parameter.So the equation for the curve
as a parameter.So the equation for the curve  is
is
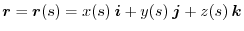
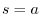 and
and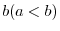 , respectively.
At this time, the scalar field defined for any point P
, respectively.
At this time, the scalar field defined for any point P 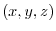 on the curve
on the curve
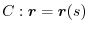 is
is
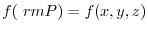 .
.
The curve  is divided into
is divided into 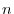 arcs
arcs
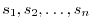 , and this division is represented by
, and this division is represented by 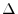 . Let the arc length of each curve
. Let the arc length of each curve 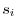 be
be
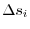 , take an arbitrary point
, take an arbitrary point
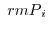 in
in 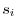 ,
,
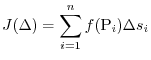
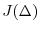 approaches the limit value
approaches the limit value 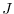 when this division is made finer and
when this division is made finer and 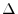 is made as small as possible, then this limit value
is made as small as possible, then this limit value 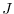 is called line integral of the scalar field
is called line integral of the scalar field 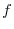 along C and denoted by
along C and denoted by
|
When the curve  is closed, it is expressed as
is closed, it is expressed as
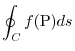
Since the definition of line integral is based on the same Riemann sum as the previous integral, it is clear that the following formula holds for line integral.
|
Also, when the curve  is not smooth but is made up of a finite number of smooth curves
is not smooth but is made up of a finite number of smooth curves
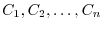 , this curve is Piecewise smooth curve , and the line integral along such a curve is
, this curve is Piecewise smooth curve , and the line integral along such a curve is
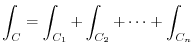
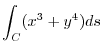 , where
, where  is a line connecting the points
is a line connecting the points  and
and 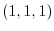 .
.
Answer
When the straight line connecting the point 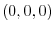 and the point
and the point 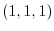 is displayed as a parameter
is displayed as a parameter
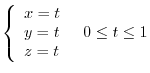
 is expressed as
is expressed as
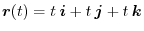 and the length
and the length 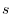 of
of  is
is
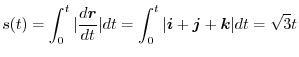
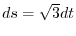 and the line integral is
and the line integral is
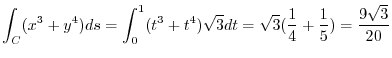
Line integral of vector field
Oriented curve
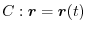 and the vector field defined on
and the vector field defined on  ,
,
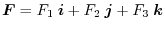 are given.Here, the unit tangent vector
are given.Here, the unit tangent vector 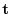 of
of  is positive direction.Then
is positive direction.Then
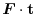 is a scalar field defined on
is a scalar field defined on  and the line integral of this scalar field on
and the line integral of this scalar field on  is expressed by
is expressed by
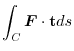
 oriented curve
oriented curve
 .EEspecially, note that
.EEspecially, note that
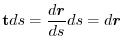
|
Considering the case where the vector field
 is an electric field.
is an electric field.
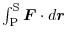 can be thought of as the work per unit charge performed by the electric field
can be thought of as the work per unit charge performed by the electric field
 . when the positive charge moves from point P to point S along the curve
. when the positive charge moves from point P to point S along the curve  , which is called the potential difference or voltage between two points.
, which is called the potential difference or voltage between two points.
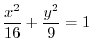 . Note that vector field is given by
. Note that vector field is given by
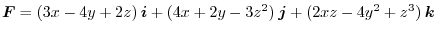
Answer
Let
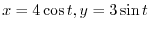 . Then
. Then
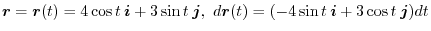
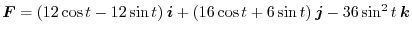
![$\displaystyle \int_{C} \boldsymbol{F} \cdot d \boldsymbol{r} = \int_{0}^{2\pi} [48 - 30\sin{t}\cos{t}]dt = 96\pi$](img492.png)
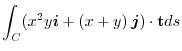 .Here,
.Here,  is the curve
is the curve
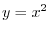 from
from 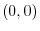 to
to 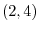 .
.
Answer
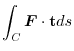 |
 |
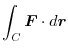 |
|
 |
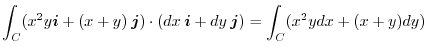 |
||
 |
![$\displaystyle \int_{0}^{2} x^2 x^2 dx + \int_{0}^{2}(x + x^2)(2xdx) = \left[\fr...
...} + \left[\frac{2}{3}x^{3} + \frac{2}{4}x^{4} \right ]_{0}^{2} = \frac{296}{15}$](img499.png) |
Alternate answer
Express the curve  using a parameter.
using a parameter.
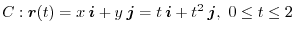
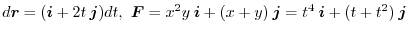
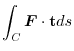 |
 |
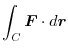 |
|
 |
![$\displaystyle \int_{0}^{2}(t^4\:\boldsymbol{i} + (t+t^2)\:\boldsymbol{j}) \cdot...
...5}t^{5} + \frac{2}{3}t^{3} + \frac{2}{4}t^{4} \right ]_{0}^{2} = \frac{296}{15}$](img502.png) |
In this example, 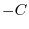 is a reversed curve of
is a reversed curve of  so that the direction is from
so that the direction is from 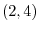 to
to 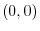 . Then
the parameteric expression of
. Then
the parameteric expression of 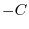 is
is
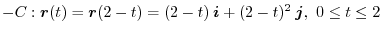
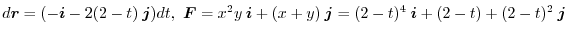
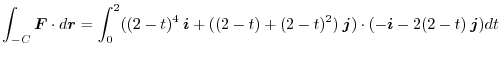
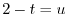 . Then
. Then 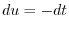 and
and
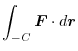 |
 |
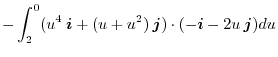 |
|
 |
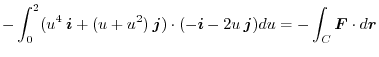 |
|
So far, in the conservation field, we have already learned that the vector field is equal in magnitude to the gradient of the scalar field. Now let's investigate what holds true in relation to line integrals.
|
Potential energy
Suppose the force field
 has the potential
has the potential 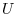 . That is, suppose
. That is, suppose
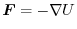 holds. Consider the curve
holds. Consider the curve  in the field of this force, and assume that the curve
in the field of this force, and assume that the curve  goes from the point P to Q..When a mass moves from point P to Q along this curve
goes from the point P to Q..When a mass moves from point P to Q along this curve  while being affected by this force field, the work
while being affected by this force field, the work 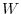 that this mass receives from
that this mass receives from
 is
is
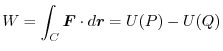
 that connects the two points P and Q.Therefore, the value
that connects the two points P and Q.Therefore, the value
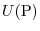 at the point P of the potential
at the point P of the potential  is called potential energy at the point P of this force field.
is called potential energy at the point P of this force field.
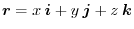 ,
,
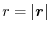 . Then show that the vector field
. Then show that the vector field
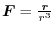 has the scalar potential
has the scalar potential
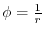 and find the potential energy at each point in space.
and find the potential energy at each point in space.
Answer
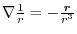 implies
implies
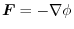 .
or,
.
or,
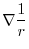 |
 |
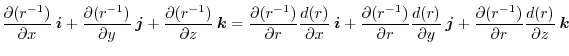 |
|
 |
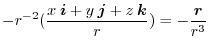 |
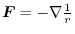 and the vector field
and the vector field
 has a potential
has a potential
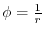 . Therefore, the potential energy at P is
. Therefore, the potential energy at P is
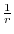 .
.
 has the potential
has the potential 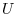 . Prove that the following equation holds when a mass point with mass
. Prove that the following equation holds when a mass point with mass 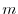 moves in this force field and moves from point A to point B.
moves in this force field and moves from point A to point B.
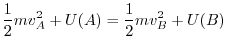
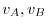 are magnitude of the velocity vectors at
are magnitude of the velocity vectors at 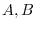 , respectively.
, respectively.
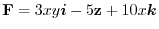 . Find the work done by
. Find the work done by
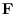 which is
which is
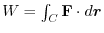 , moving along the curve
, moving along the curve
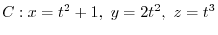
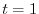 to
to 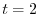 .
.
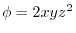 ,the field
,the field
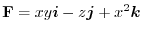 . Let the curve
. Let the curve  be parametrized by
be parametrized by
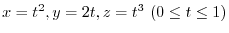 .Find the following line integrals.
.Find the following line integrals.
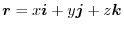 .Then for any closed curve
.Then for any closed curve  , prove that
, prove that
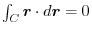 .
.
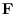 has the potential
has the potential 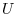 .Within the force field, the point mass with the mass
.Within the force field, the point mass with the mass 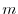 moves from the point A to the point B, show that following equation holds.
moves from the point A to the point B, show that following equation holds.
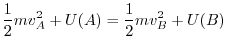
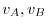 are the magnitude of velocity vectors of A and B.
are the magnitude of velocity vectors of A and B.
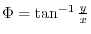 is defined in the domain
is defined in the domain 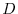 excluding the
excluding the 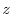 axis from the whole space.
Let
axis from the whole space.
Let  be a circle with a radius of
be a circle with a radius of 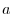 centered at the origin O on the
centered at the origin O on the 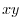 plane. Prove the following equation.
plane. Prove the following equation.