Next: Index Up: Introduction to Vector Analysis Previous: Stokes'theorem Contents Index
1.
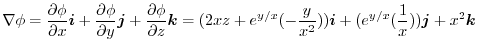
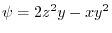 implies,
implies,
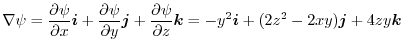
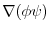 |
 |
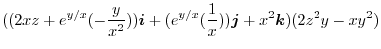 |
|
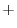 |
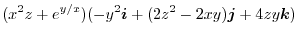 |
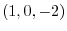 is
is
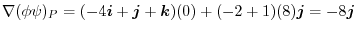
2. The directional derivative of  at P
at P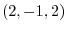 in the direction of
in the direction of 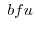 is,
is,
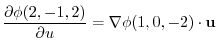
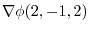 |
 |
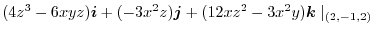 |
|
 |
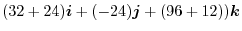 |
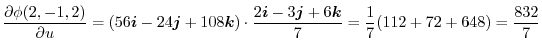
3. Use
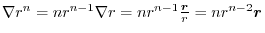
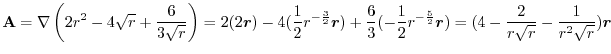
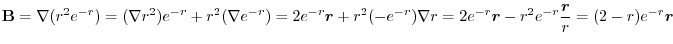
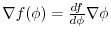 , we have
, we have
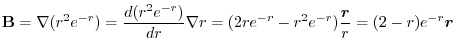
4. Note that
 of
of
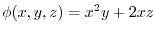 is orthogonal to
is orthogonal to
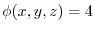 .Therefore the unit normal vector
.Therefore the unit normal vector
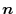 is
is
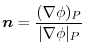
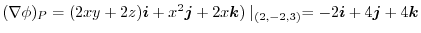 implies
implies
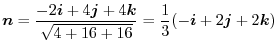
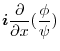 |
 |
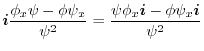 |
|
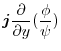 |
 |
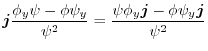 |
|
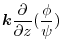 |
 |
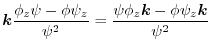 |
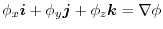 ,
,
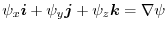 . Thus,
. Thus,
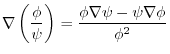
6.
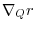 |
 |
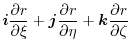 |
|
 |
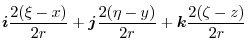 |
||
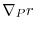 |
 |
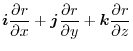 |
|
 |
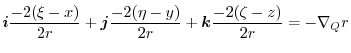 |
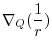 |
 |
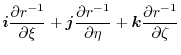 |
|
 |
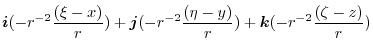 |
||
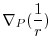 |
 |
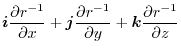 |
|
 |
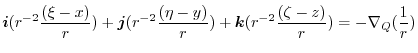 |
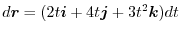
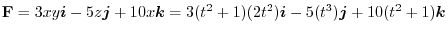 .
Therefore,
.
Therefore,
 |
 |
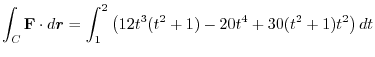 |
|
 |
![$\displaystyle \int_{1}^{2} (12t^5 + 10t^4 + 12t^3 + 30t^2 )dt = \left[2t^6 + 2t^5 + 3t^4 + 10t^3\right]_{1}^{2}$](img1096.png) |
||
 |
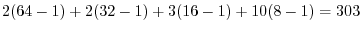 |
2.
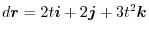
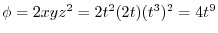 .Therefore,
.Therefore,
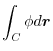 |
 |
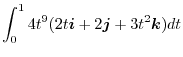 |
|
 |
![$\displaystyle \int_{0}^{1}(8t^{10}\boldsymbol{i} + 8t^{9}\boldsymbol{j} + 12t^{...
...bol{i} + \frac{8}{10}t^{10}\boldsymbol{j} + t^{12}\boldsymbol{k}\right]_{0}^{1}$](img1103.png) |
||
 |
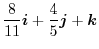 |
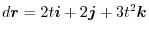
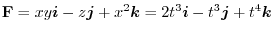 .Therefore,
.Therefore,
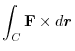 |
 |
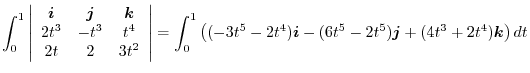 |
|
 |
![$\displaystyle \left[(-\frac{t^6}{2} - \frac{2t^5}{5})\boldsymbol{i} - \frac{4t^6}{6}\boldsymbol{j} + (t^4 + \frac{2t^5}{5})\boldsymbol{k}\right]_{0}^{1}$](img1108.png) |
||
 |
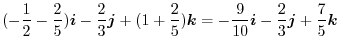 |
3. Note that if 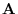 satisfies
satisfies
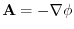 ,then
,then 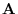 has a scalar potential and
has a scalar potential and
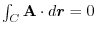 . Thus we find
. Thus we find  so that,
so that,
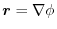 .
.
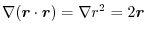
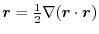 .Therefore,
.Therefore,
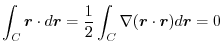
4. The force field
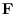 has a potential
has a potential 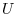 . Then
. Then
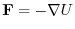 .This suggest that the equation of motion of this mass point is
.This suggest that the equation of motion of this mass point is
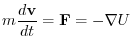
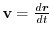 .Then
.Then
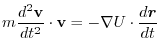
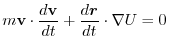
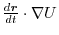 .
.
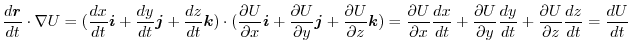
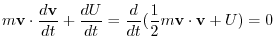
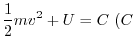 constant
constant
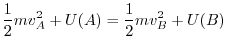
5.
If the origin O is centered on this  plane and the circle with radius
plane and the circle with radius 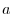 is
is  , the equation of motion of the mass point is parametrized by
, the equation of motion of the mass point is parametrized by
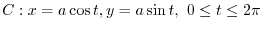 .Thus,
.Thus,
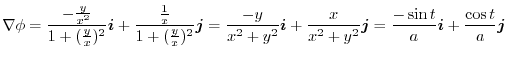
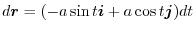
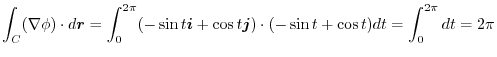
Exercise Answer3.4
1.
(1) When the curved surface  is projected onto the
is projected onto the  plane,
plane, maps to
maps to
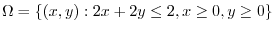 . Also,from the surface
. Also,from the surface
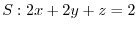 , if the corresponding
, if the corresponding
 is the position vector,
is the position vector,
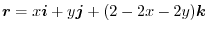
 which is
which is
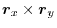 ,
,
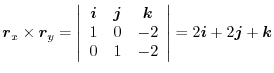
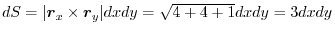 . Then
. Then
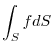 |
 |
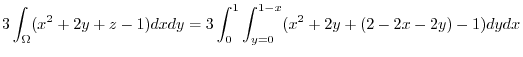 |
|
 |
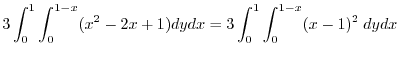 |
||
 |
![$\displaystyle 3\int_{0}^{1}\left[(x-1)^2y\right]_{0}^{1-x}dx = 3\int_{0}^{1}(1-x)^3\;dx = -3\left[\frac{1}{4}(1-x)^{4}\right]_{0}^{1} = \frac{3}{4}$](img1137.png) |
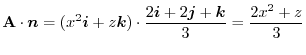
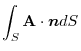 |
 |
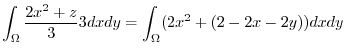 |
|
 |
![$\displaystyle \int_{0}^{1}\int_{0}^{1-x}(2x^2 - 2x - 2y + 2)dy dx = \int_{0}^{1}\left[2x^2 y - 2xy -y^2 + 2y\right]_{0}^{1-x}dx$](img1143.png) |
||
 |
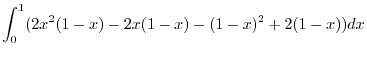 |
||
 |
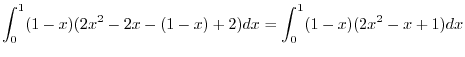 |
||
 |
![$\displaystyle \int_{0}^{1}(-2x^3 +3x^2 - 2x + 1)dx = \left[-\frac{x^4}{2} + x^3 - x^2 + x\right]_{0}^{1}$](img1146.png) |
||
 |
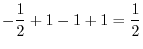 |
2. Since the surface  is region on the
is region on the 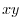 plane,the unit normal vector is
plane,the unit normal vector is
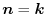 .
.
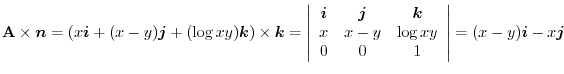
 is on the
is on the 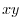 plane. Then
plane. Then
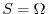 ,
,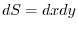 .Here,
.Here,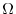 is a disk, so we use the polar coordinates, then
is a disk, so we use the polar coordinates, then
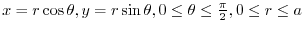 and
and
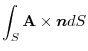 |
 |
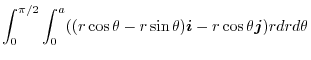 |
|
 |
![$\displaystyle \int_{0}^{\pi/2}\left[\frac{r^3}{3}\right]_{0}^{a}\left((\cos{\theta} - \sin{\theta})\boldsymbol{i} - \cos{\theta}\boldsymbol{j}\right)d\theta$](img1155.png) |
||
 |
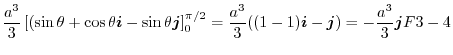 |
3. By projecting  onto
onto  plane, then
plane, then  aps to
aps to
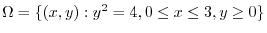 .
Next by letting
.
Next by letting 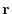 be a position vector
be a position vector
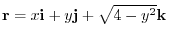 .
Thus,the normal vector of the surface
.
Thus,the normal vector of the surface  is
is
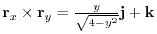 .
Therefore,,
.
Therefore,,
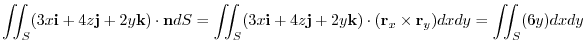
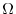 using vertical simple, we have,
using vertical simple, we have,
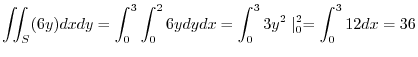
4. By projecting the surface  onto
onto  plane,
plane,  maps to
maps to
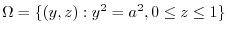 .
Next,let
.
Next,let 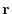 be a postion vector
be a postion vector
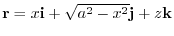 .
Thus,the normal vector of
.
Thus,the normal vector of  is
is
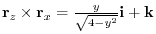 .
.
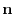 |
 |
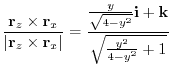 |
|
 |
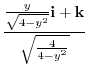 |
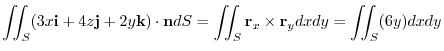
 using the vertical simple,
using the vertical simple,
Exercise Answer3.5
Basic formula Let
 . Then (1)
. Then (1)
1.
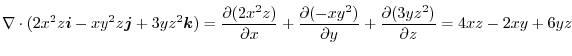
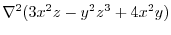 |
 |
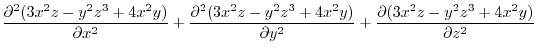 |
|
 |
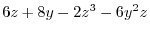 |
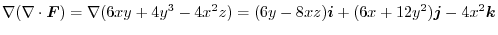
2.
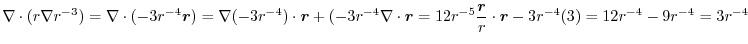
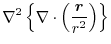 |
 |
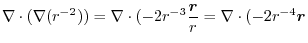 |
|
 |
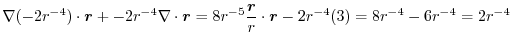 |
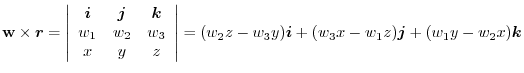
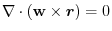
4.
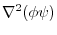 |
 |
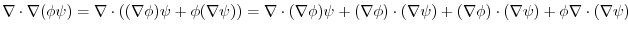 |
|
 |
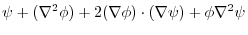 |
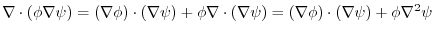 |
(3) (2) implies,
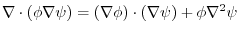 . By symmetry
. By symmetry
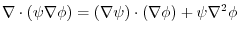 . Therefore,
. Therefore,
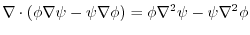 |
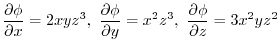
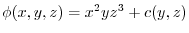 .Here using
.Here using
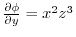 ,
,
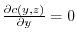 . Then
. Then
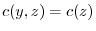 .Finally,
.Finally,
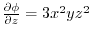 implies
implies
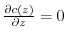 . Then
. Then 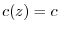 .Thus,
.Thus,
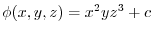 . Now by the initial value
. Now by the initial value
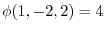 , we have
, we have 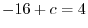 and
and 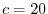 .
.
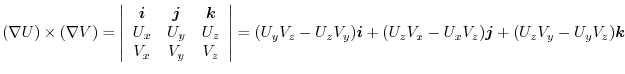
 |
 |
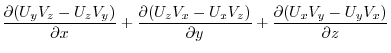 |
|
 |
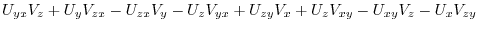 |
||
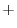 |
 |
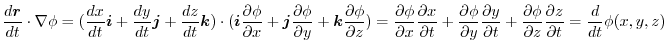
![\includegraphics[width = 4cm]{VECANALFIG/3-5-8.eps}](img1207.png)
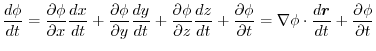
Exercise詳Answer3.6
1.
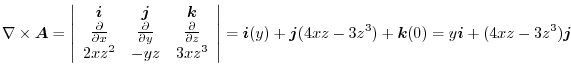
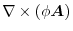 |
 |
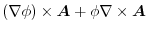 |
|
 |
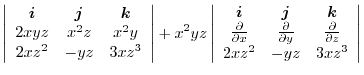 |
||
 |
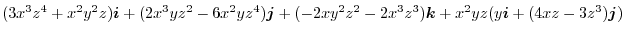 |
||
 |
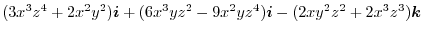 |
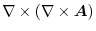 |
 |
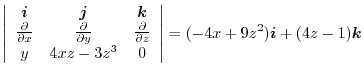 |
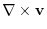 |
 |
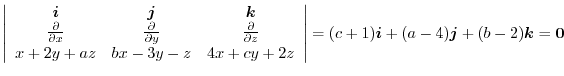 |
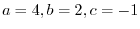
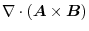 |
 |
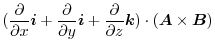 |
|
 |
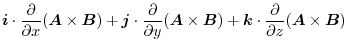 |
||
 |
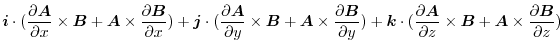 |
||
 |
![$\displaystyle \boldsymbol{B}\cdot(\boldsymbol{i} \times \frac{\partial \boldsym...
...\frac{\partial \boldsymbol{A}}{\partial z})\ \hskip 1cm ([A\ B\ C] = [C\ A\ B])$](img1225.png) |
||
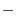 |
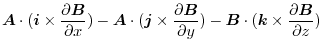 |
||
 |
 |
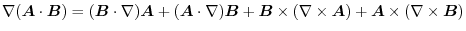
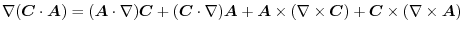
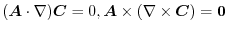 implies
implies
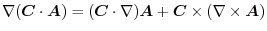
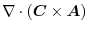 |
 |
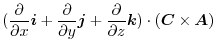 |
|
 |
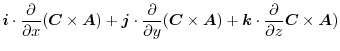 |
||
 |
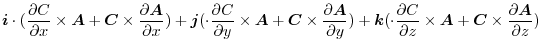 |
||
 |
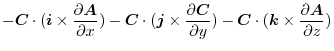 |
||
 |
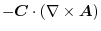 |
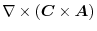 |
 |
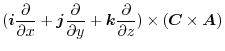 |
|
 |
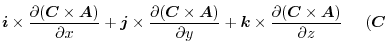 constant vector constant vector |
||
 |
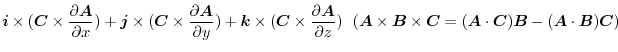 |
||
 |
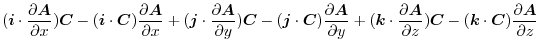 |
||
 |
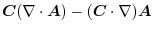 |
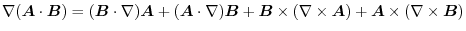
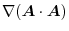 |
 |
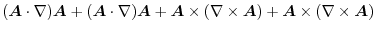 |
|
 |
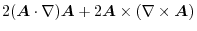 |
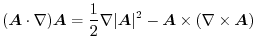
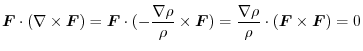
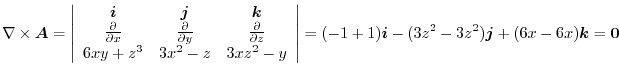
Note that there exits  so that
so that
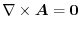 implies
implies
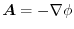 .
.
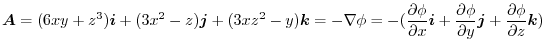
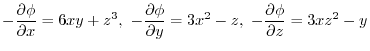
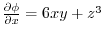 implies
implies
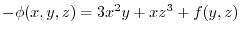 .Now partially differentiate
.Now partially differentiate  by
by 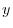 ,
,
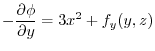
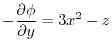
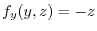
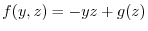 .Thus,
.Thus,
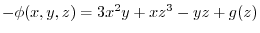 .
Here partially differentiate
.
Here partially differentiate
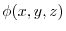 by
by 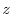 ,
,
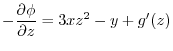
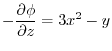
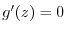
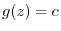 and
and
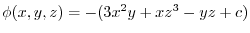
Exercise Answer4.1
1.
(1) Gauss's divergence theorem implies
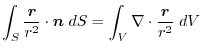
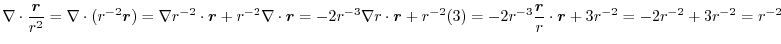
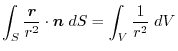
(2) Tranform
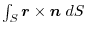 into the surface integral.Usiing any constant vetor
into the surface integral.Usiing any constant vetor
 and the triple scalar product,
and the triple scalar product,
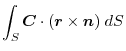 |
 |
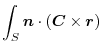 |
|
 |
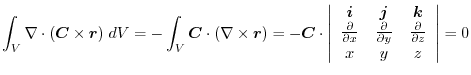 |
 is a constant vector implies
is a constant vector implies
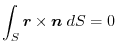
(3) Gauss's dievergence theorem implies
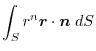 |
 |
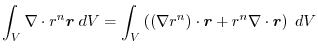 |
|
 |
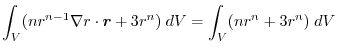 |
||
 |
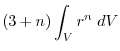 |
(4) Transfrom
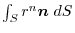 into surface integral.Using a constant vector
into surface integral.Using a constant vector
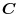 ,
,
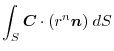 |
 |
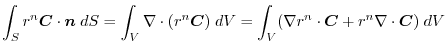 |
|
 |
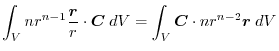 |
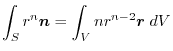
(5) Transform
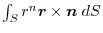 into surface integral.Using a constant vector
into surface integral.Using a constant vector
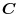 and the triple scalar product,
and the triple scalar product,
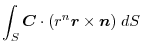 |
 |
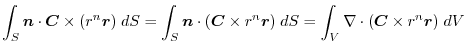 |
|
 |
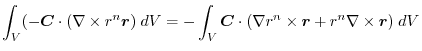 |
||
 |
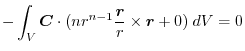 |
(6) Transform
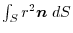 into surface integral.Using a constant vector
into surface integral.Using a constant vector
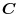 , we have
, we have
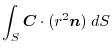 |
 |
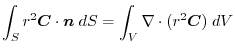 |
|
 |
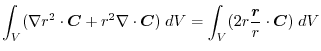 |
||
 |
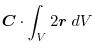 |
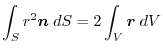
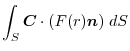 |
 |
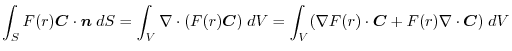 |
|
 |
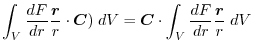 |
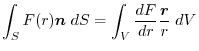
2. Using
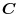 ,we write into surfacee integral.
,we write into surfacee integral.
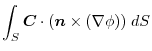 |
 |
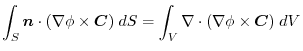 |
|
 |
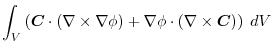 |
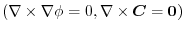 .
.
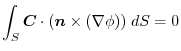
3. Let  be the boundary of the curved surface
be the boundary of the curved surface  , and let
, and let  and
and  be the curved surfaces separated by the boundary. Also,let the unit normal vector of
be the curved surfaces separated by the boundary. Also,let the unit normal vector of  be
be
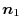 ,the unt normal vector of
,the unt normal vector of  be
be
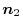 .Then let the unit normal vector of the surface
.Then let the unit normal vector of the surface  be
be
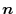 . We have
. We have
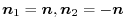 or
or
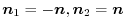 .Here, ,
.Here, ,
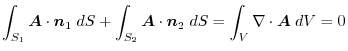
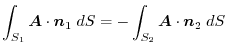
4.
(1) Gauss's divergence theorem implies
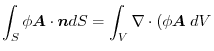
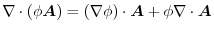 .
.
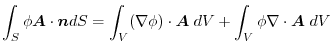
(2) Gauss's divergence theorem implies
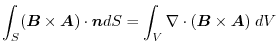
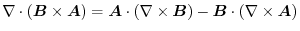 .Thus,
.Thus,
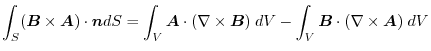
(3) Gauss's divergence theorem implies
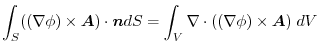
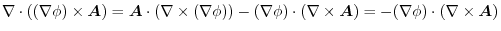
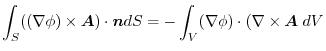
(4) Gauss's divergence theorem implies
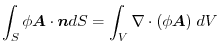
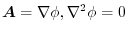 implies
implies
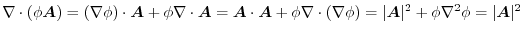
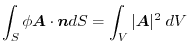
5.
(1)
labelenshu:4-1-5-1
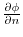 is the directional derivative of the direction of unit normal vector
is the directional derivative of the direction of unit normal vector
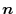 implies
implies
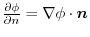 .Thus,
.Thus,
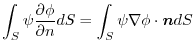
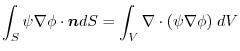
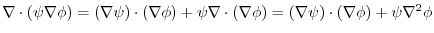 implies
implies
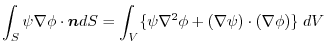
(2)
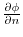 is the directional derivative of the direction of unit normal vector implies
is the directional derivative of the direction of unit normal vector implies
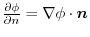 .Thus,
.Thus,
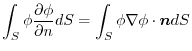
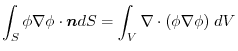
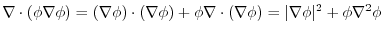 implies
implies
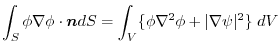
(3) The result of (1) subtracts the result of (2). Then,
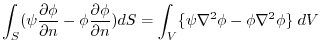
(4)  is harmonic function means that
is harmonic function means that
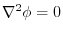 .Therefore,using (2),
.Therefore,using (2),
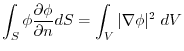
(5)
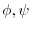 are harmonic functions means that
are harmonic functions means that
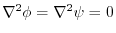 .Therefore,using (3),
.Therefore,using (3),
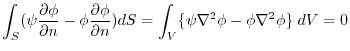
(6)  is harmonic function. Then (4)implies
is harmonic function. Then (4)implies
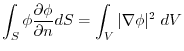
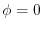 on
on  . Then
. Then
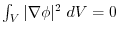 and
and
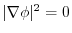 .Thus,
.Thus,
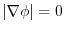 . Hence,
. Hence,
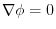 .Therefore,
.Therefore, は定数.
は定数.
6. If
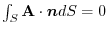 ,then Gauss's divergence theorem implies
,then Gauss's divergence theorem implies
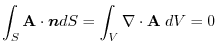
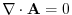 . The theorem 3.4 implies
. The theorem 3.4 implies 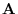 has a vector potential.
has a vector potential.
7.
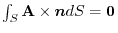 .Here, using a constant vector
.Here, using a constant vector 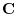 , rewrite into surface integral.
, rewrite into surface integral.
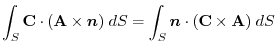
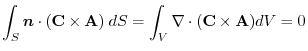
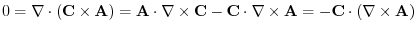
 and
and  has a scalar potential.
has a scalar potential.
Exercise Answer4.2
1.
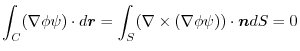
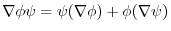
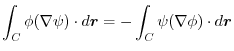
2.
(1) Rewrite a line integral into
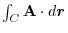 .To do so, using a constant vector
.To do so, using a constant vector 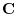 and the triple scalar product,we have
and the triple scalar product,we have
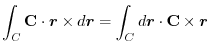
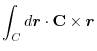 |
 |
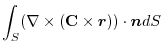 |
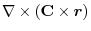 |
 |
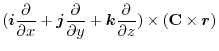 |
|
 |
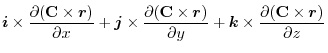 |
||
 |
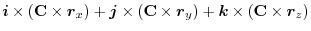 |
||
 |
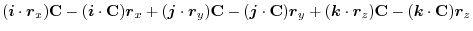 |
||
 |
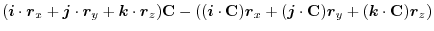 |
||
 |
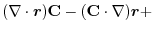 |
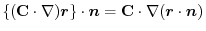
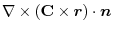 |
 |
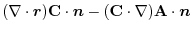 |
|
 |
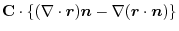 |
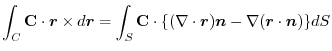
 is a constant vector. Then,
is a constant vector. Then,
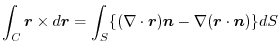
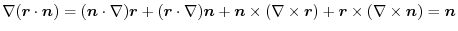
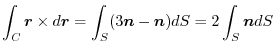
 |
 |
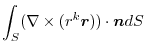 |
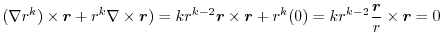
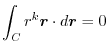
(3) Let  be a constant vector. Then using Stokes' theorem,
be a constant vector. Then using Stokes' theorem,
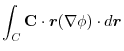 |
 |
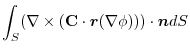 |
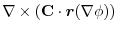 |
 |
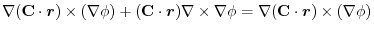 |
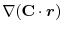 |
 |
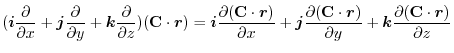 |
|
 |
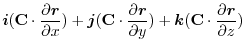 |
||
 |
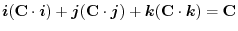 |
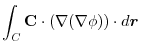 |
 |
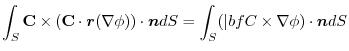 |
|
 |
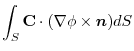 |
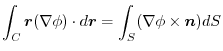
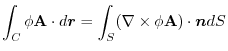
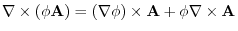
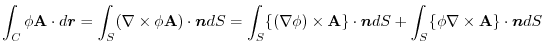
4. Rewrite the line integral into
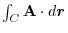 .Then using a constant vector
.Then using a constant vector 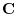 and the triple scalar product,and Stokes' theorem,we have
and the triple scalar product,and Stokes' theorem,we have
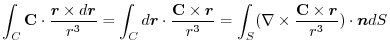
Here using the triple scalar product, we have
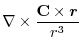 |
 |
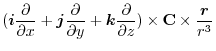 |
|
 |
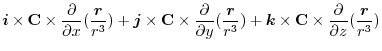 |
||
 |
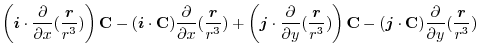 |
||
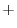 |
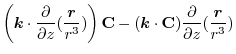 |
||
 |
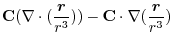 |
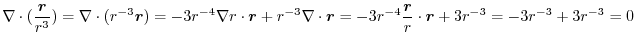
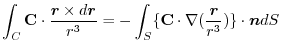
 is a constant vector.
is a constant vector.
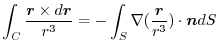
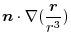 |
 |
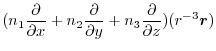 |
|
 |
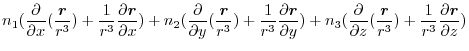 |
||
 |
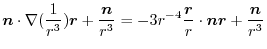 |
||
 |
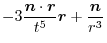 |
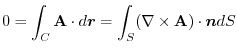
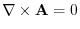 .Therefore,
.Therefore,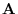 has a scalar potential.
has a scalar potential.