Next: Exercise Answer Up: Integral formula Previous: Gauss's divergence theorem Contents Index
Stokes' theorem
A generalization of Green's theorem by Irish mathematician and physicist George Gabriel Stokes (1819-1903) is called Stokes' theorem.First, To study Stokes' theorem, we need to orient the surface..
Stokes' theorem gives an equation that rewrites the line integral along the bounding curve
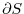 of the oriented surface
of the oriented surface  to the surface integral on
to the surface integral on  .
.
|
Proof
Firsr consider
![$\iint_{S} [\nabla \times F_{1}\boldsymbol{i}] \cdot\boldsymbol{n}dS$](img959.png) .
.
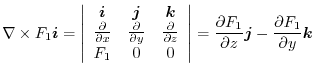
![$\boldsymbol{r} = {}^t[x,y,z]$](img962.png) be a position vector. Then
be a position vector. Then
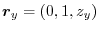 is a tangent vector of
is a tangent vector of  . Thus it is orthogonal to the normal vecto
. Thus it is orthogonal to the normal vecto
 .
.
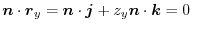 or
or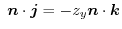
![$\displaystyle [\nabla \times F_{1}\boldsymbol{i}] \cdot\boldsymbol{n}dS = - \le...
...ac{\partial F_{1}}{\partial y} \right ) \boldsymbol{n} \cdot \boldsymbol{k} dS $](img966.png)
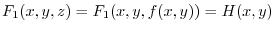 on
on  . Thus by the differentiation of composite functions, we have
. Thus by the differentiation of composite functions, we have
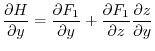
![$\displaystyle [\nabla \times F_{1}\boldsymbol{i}] \cdot\boldsymbol{n}dS = - \fr...
...}\boldsymbol{n} \cdot \boldsymbol{k} dS = - \frac{\partial H}{\partial y}dx dy $](img969.png)
![$\displaystyle \iint_{S}[\nabla \times F_{1}\boldsymbol{i}] \cdot\boldsymbol{n}dS = \iint_{\Omega}- \frac{\partial H}{\partial y}dx dy $](img970.png)
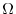 is a normal projection of
is a normal projection of  on the
on the 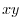 plane. The integral on the right is the integral on the plane, which is
plane. The integral on the right is the integral on the plane, which is
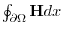 according to Green's theorem.
The value of
according to Green's theorem.
The value of 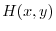 at the point
at the point 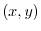 on the boundary of
on the boundary of 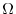 and at the point
and at the point 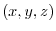 on the boundary of
on the boundary of  The values of
The values of
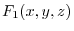 are equal, and
are equal, and 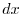 is the same for both curves.
is the same for both curves.
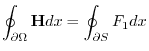
![$\displaystyle \iint_{S}[\nabla \times F_{1}\boldsymbol{i}] \cdot\boldsymbol{n}dS = \oint_{\partial S}{F_{1}}dx $](img976.png)
![$\displaystyle \iint_{S}[\nabla \times F_{2}\boldsymbol{j}] \cdot\boldsymbol{n}d...
...times F_{3}\boldsymbol{k}] \cdot\boldsymbol{n}dS = \oint_{\partial S}{F_{3}}dz $](img977.png)
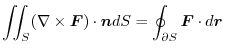
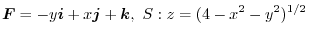 ,show that Stokes' theorem holds.
,show that Stokes' theorem holds.
Answer
The boundary of  ,
,
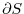 is a circle
is a circle
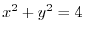 .Thus the position vector is
.Thus the position vector is
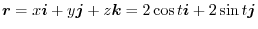 . Then we find the line integral
. Then we find the line integral
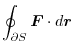 |
 |
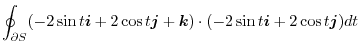 |
|
 |
![$\displaystyle \int_{0}^{2\pi}[4\sin^{2}{t} + 4\cos^{2}{t}]dt = 8\pi$](img984.png) |
Next we find the surface integral..
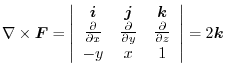
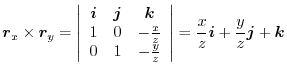
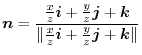
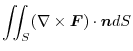 |
 |
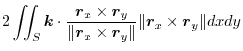 |
|
 |
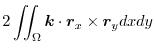 |
||
 |
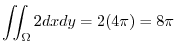 |
So far we have already learned that in a conservative field, the vector field is equal to the gradient of the scalar field, and the rotation of the vector field is zero. Now let's investigate what holds true in relation to line integrals.
|
Proof Show
(1)
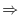 (2)
(2)
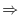 (3)
(3)
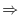 (1).
(1).
(1)
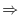 (2)
(2)
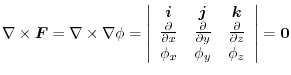
(2)
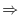 (3) Consider the surface
(3) Consider the surface  bounded by
bounded by  and apply Stokes' theorem.
and apply Stokes' theorem.
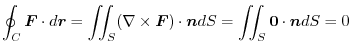
(3)
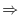 (1) Two curves
(1) Two curves
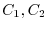 connecting the fixed point P
connecting the fixed point P
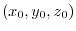 and the moving point Q
and the moving point Q 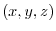 . Starting from P passing
. Starting from P passing 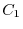 to Q and from Q passing
to Q and from Q passing 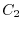 to P. Set this whole path
to P. Set this whole path  .
.
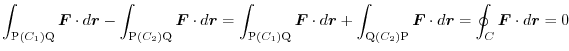
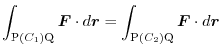
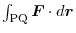 is given by the function of the coordinate
is given by the function of the coordinate 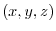 of the end point Q regardless of the route in the middle. So if you set this to
of the end point Q regardless of the route in the middle. So if you set this to
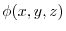 , then we have
, then we have
|
We let vector equation for any curve from P to Q as
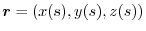 . Then
. Then
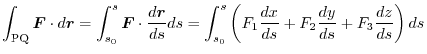
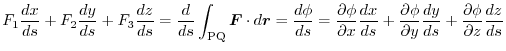
 is also an arbitrary function.,
is also an arbitrary function.,
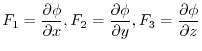
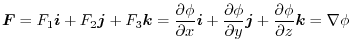
From this theorem, we can see that the answer is 0 even without integration if the vector field has a scalar potential when performing line integrals
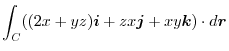 .where
.where  is a curve connecting from the point
is a curve connecting from the point 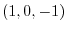 to
to 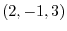 and back to the starting point..
and back to the starting point..
Answer
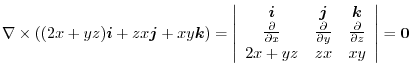
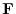 has a scalar potential.So, we find
has a scalar potential.So, we find 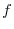 so that
so that
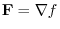 .
.
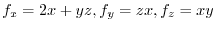 implies
implies
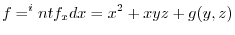
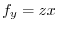 imlies
imlies
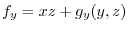 . Thus,
. Thus,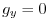 . in other words,
. in other words,
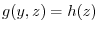 . Next,
. Next,
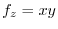 implies
implies
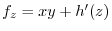 . Thus
. Thus 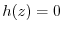 .Here,let
.Here,let 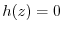 . Then
. Then
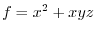
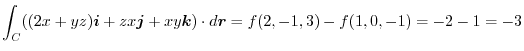
 and its boundary
and its boundary  within the common domain of
within the common domain of
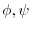 , prove the following equation holds.
, prove the following equation holds.
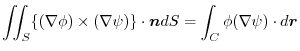
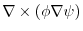 .
.
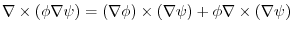
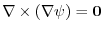 implies
implies
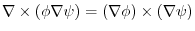
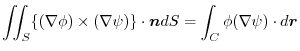
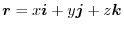 .Prove for any surface
.Prove for any surface  and its boundary
and its boundary  , the following is true.
, the following is true.
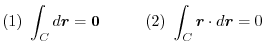
 and its boundary
and its boundary  in the common domain of the scalar fields
in the common domain of the scalar fields 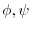 ..
..
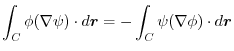
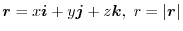 and
and  be a scalar field. Then prove the following equation holds for any surface
be a scalar field. Then prove the following equation holds for any surface  and its boundary
and its boundary  .
.
 and its boundary
and its boundary  in the common domain of the scalar field
in the common domain of the scalar field  and the vector field
and the vector field 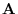 .
.
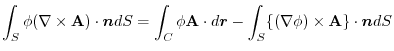
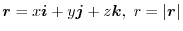 and
and  be a scalar field. Prove that for any surface
be a scalar field. Prove that for any surface  and its boundary
and its boundary  , the following equation holds.
, the following equation holds.
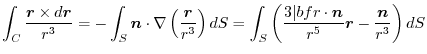
 is defined in the whole space..About the border
is defined in the whole space..About the border  of any curved surface if
of any curved surface if
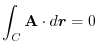
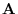 has a scalar potential. Prove this.
has a scalar potential. Prove this.