Next: Stokes'theorem Up: Integral formula Previous: Integral formula Contents Index
Gauss's divergence theorem
Proof First, suppose 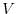 is sandwiched between two curved surfaces
is sandwiched between two curved surfaces
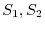 from the bottom and top..Also,
from the bottom and top..Also, 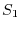 is given by
is given by
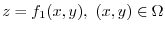 ,
,  is given by
is given by
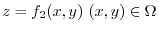 . Then
. Then
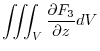 |
 |
![$\displaystyle \iiint_{V}\frac{\partial F_{3}}{\partial z} dzdydx = \iint_{\Omega}[\int_{z=f_{1}(x,y)}^{f_{2}(x,y)}\frac{\partial F_{3}}{\partial z} dz] dydx$](img848.png) |
|
 |
![$\displaystyle \iint_{\Omega}\left[F_{3}\right ]_{z = f_{1}(x,y)}^{f_{2}(x,y)}dydx$](img849.png) |
||
 |
![$\displaystyle \iint_{\Omega}[F_{3}(x,y,f_{2}(x,y)) - F_{3}(x,y,f_{1}(x,y)) ]dy dx$](img850.png) |
 ,normal unit vector for curvilinear coordinates
,normal unit vector for curvilinear coordinates 
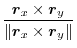
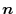 . On the surface
. On the surface 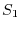 , the unit normal vector is equal to
, the unit normal vector is equal to
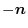 . Thus,
. Thus,
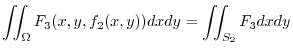
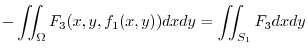
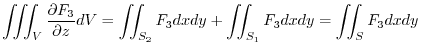
 onto another plane, we can show
onto another plane, we can show
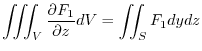
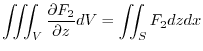
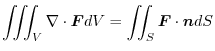
If the region  is common, you can prove it by dividing
is common, you can prove it by dividing  into subregions
into subregions
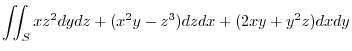
 is the upper sphere
is the upper sphere
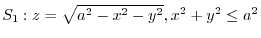 と
と
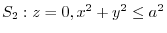 .
.
(1) Evaluate this surface integral by using Gauss's divergence theorem.
(2) Evaluate this surface integral directly.
Answer (1)
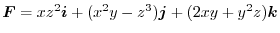 より
より
 を求めると
を求めると
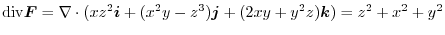
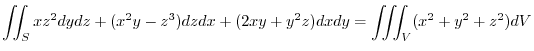
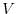 is an upper sphere with the radius
is an upper sphere with the radius 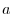 . Then by the spherical coordinate transformation
. Then by the spherical coordinate transformation
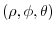 , we have
, we have
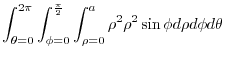 |
 |
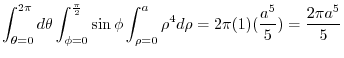 |
(2)
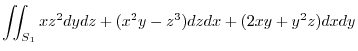 |
 |
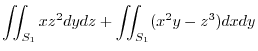 |
|
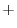 |
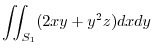 |
Since
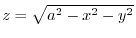 ,projection onto
,projection onto 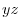 plane,
plane,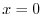 implies
implies
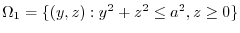 . Here,we consier
. Here,we consier 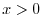 and
and 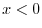 .
.
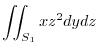 |
 |
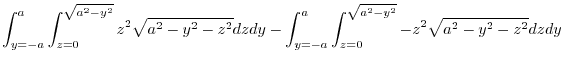 |
|
 |
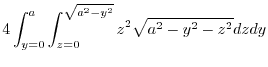 |
Next projection onto 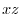 plane. Then
plane. Then 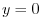 implies
implies
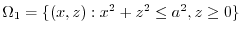 .Thus,for
.Thus,for 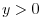 and
and 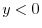 ,
,
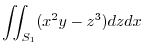 |
 |
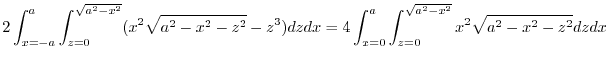 |
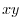 plane. Then
plane. Then 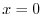 implies
implies
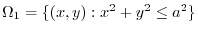 .
.
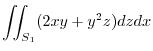 |
 |
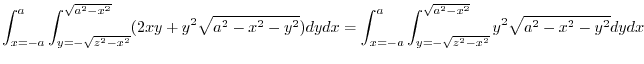 |
|
 |
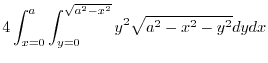 |
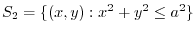 .First projection onto,
.First projection onto,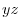 plane.
plane.  maps to
maps to
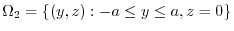 .
.
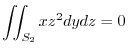
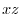 plane,
plane, maps to
maps to
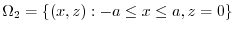 .,
.,
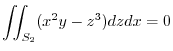
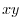 plane,
plane,  maps to
maps to
 .
.
Adding these,
 |
 |
 |
|
 |
 |
Here using the polar coorinates,we have
 . Thus
. Thus
 |
 |
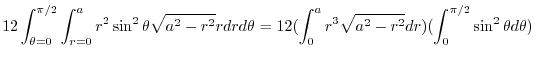 |
|
 |
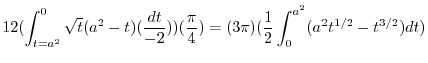 |
||
 |
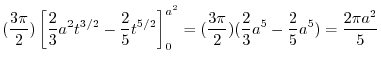 |
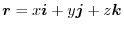 .Show the followings for the region
.Show the followings for the region 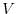 and the boundary surface
and the boundary surface  . Here, denote the vaolume of the region
. Here, denote the vaolume of the region 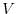 by
by 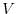 .
.
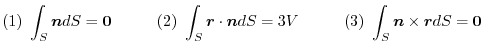
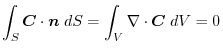
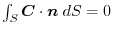
(2) By Gauss's divergence theorem,
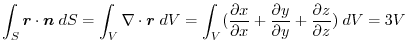
(3) Using a constant vector,we express by the surface integral and apply the triple scalar product and Gauss's divergance theorem,
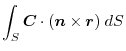 |
 |
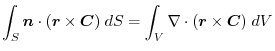 |
|
 |
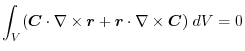 |
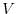 in the scalar field
in the scalar field  and its boundary surface
and its boundary surface  .
.
(1)
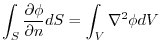
(2) If  is a harmonic function, then
is a harmonic function, then
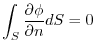
Answer
(1) The problem of surface integral is always rewrite into
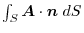 .In this case,
.In this case,
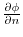 isa directional derivative in the direction of the unit normal vector
isa directional derivative in the direction of the unit normal vector
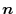 . Then
. Then
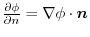 .Therefore,,
.Therefore,,
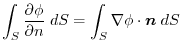
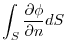 |
 |
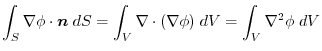 |
(2)  is harmonic function. Then
is harmonic function. Then
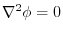 . Thus,(1) implies
. Thus,(1) implies
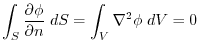
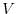 and its bounary surface
and its bounary surface  within the common definition of the scalar field
within the common definition of the scalar field  and the vector field
and the vector field
 , if
, if
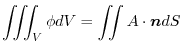
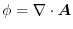 .
Proof By Gauss's divergence theorem,
.
Proof By Gauss's divergence theorem,
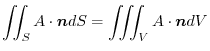
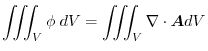
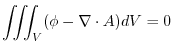
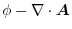 is a continuous function and for any region
is a continuous function and for any region 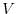 , the followings are true. Thus by the properties of the continuous function, we have
, the followings are true. Thus by the properties of the continuous function, we have
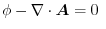 in other words
in other words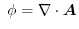
 of any region
of any region 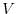 in
in
 , prove that if
, prove that if
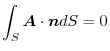
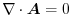 .
.
Proof If 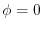 in the above theorem,then
in the above theorem,then
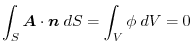
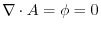 .
.
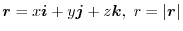 .Prove that for any region
.Prove that for any region 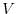 and the boundary surface
and the boundary surface  , the followings are true.
, the followings are true.
 of any region
of any region 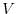 in the scalar field
in the scalar field .
.
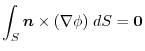
 satisfies
satisfies
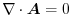 .Take the closed curve
.Take the closed curve  that is the boundary of the curved surface
that is the boundary of the curved surface  in this vector field.At this time, the surface integral
in this vector field.At this time, the surface integral
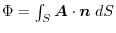 is always the same value for any curved surface
is always the same value for any curved surface  whose boundary is
whose boundary is  . And its value is determined by the closed surface
. And its value is determined by the closed surface  .Prove the above.
.Prove the above.
 and the vector field
and the vector field
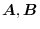 are within the comon domain. Prove the following equation for any region
are within the comon domain. Prove the following equation for any region 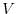 and its bounary surface
and its bounary surface  .
.
(4)
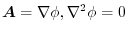 ならば,
ならば,
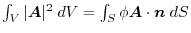
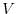 and its boundary surface
and its boundary surface  within the common definition of the scalar fields
within the common definition of the scalar fields  and
and 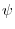 .
.
(3)
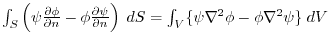 Green's formula
Green's formula
(4) If  is harmonic function, then
is harmonic function, then
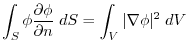
(5) If
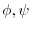 are harmonic functions, then
are harmonic functions, then
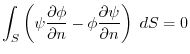
(6) If 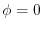 on
on  ,then the harmonic function
,then the harmonic function  is 0 in
is 0 in 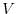 .
.
 is defined in all space. Prove that if
is defined in all space. Prove that if
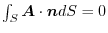 for any boundary surface
for any boundary surface  ,then
,then
 has a vector potential.
has a vector potential.
 is defined for all space. Prove that if
is defined for all space. Prove that if
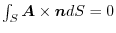 for any boundary surface
for any boundary surface  ,then
,then
 has a scalar potential.
has a scalar potential.