Next: Integral formula Up: Scalar field, vector field Previous: Divergence Contents Index
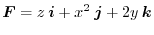 .
.
Answer
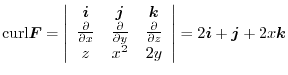
It is not so difficult to find the rotation of the vector field, but it is difficult to understand what the rotation of the vector field is. So let's understand what the rotation of a vector field is by considering the following example.
For
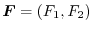 ,we study how much quadrilateral ABCD can be rotated, where quadrilateral ABCD are given by A
,we study how much quadrilateral ABCD can be rotated, where quadrilateral ABCD are given by A
 , B
, B
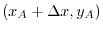 , C
, C
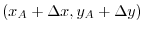 , D
, D
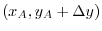
First,the horizontal component at point A
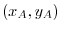 is
is
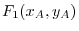 .
The horizontal component at point D
.
The horizontal component at point D
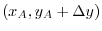 is
is
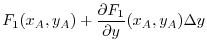
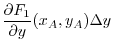 is positive, the quadrilateral ABCD rotates clockwise.
Also, the difference in the vertical components at points A and B,
is positive, the quadrilateral ABCD rotates clockwise.
Also, the difference in the vertical components at points A and B,
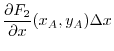 is positive,the quadrilateral ABCD rotates counter clockwise.Thus
is positive,the quadrilateral ABCD rotates counter clockwise.Thus
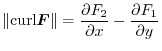
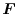 and the direction of the force is orthogonal to the quadrilateral
and the direction of the force is orthogonal to the quadrilateral
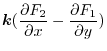 . This is the name curl comes from.Thus, for
. This is the name curl comes from.Thus, for
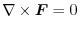 , the vector field
, the vector field
 becomes no votex.
.
becomes no votex.
.
 is conservative, show that
is conservative, show that
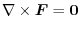 .
.
Answer
Since
 is conservative, there exists
is conservative, there exists 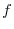 so that
so that
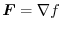 .Now we find
.Now we find
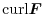 . Then
. Then
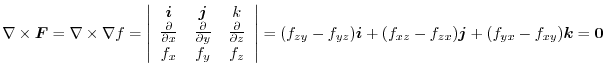
 and any vector field
and any vector field
 , show that
, show that

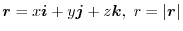 and
and
 be a constant vector, prove the followings..
be a constant vector, prove the followings..
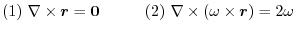
(1)
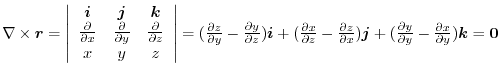
(2) Let
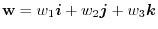 . Then
. Then
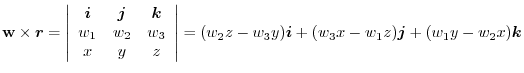
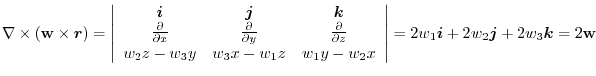
Scalar potential
If vector field
 has the potential
has the potential  ,then
,then
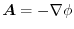 . Thus by the theorem 3.2,
. Thus by the theorem 3.2,
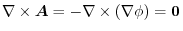 .How about the converse?.
.How about the converse?.
 on all spacesatisfies
on all spacesatisfies
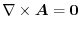 ,then the vector field
,then the vector field
 has a potential
has a potential
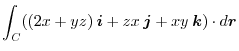 . for
. for
 is a close curve
is a close curve
 is a curve connecting from the point
is a curve connecting from the point
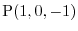 to the point
to the point
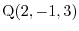 .
.
Answer (1)
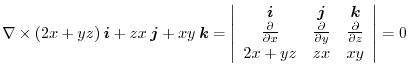
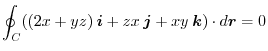
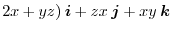 has a scalar potential, we find the scalar potential.
has a scalar potential, we find the scalar potential.
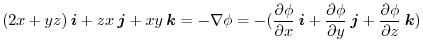
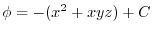 .Note that
.Note that
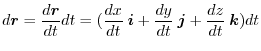
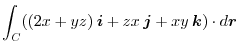 |
 |
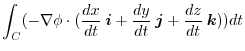 |
|
 |
![$\displaystyle \int_{{\rm P}}^{{\rm Q}}(-d \phi) = -\phi]_{P}^{Q} = (x^2 + xyz)]_{P}^{Q} = 4-6 - 1 = -3$](img802.png) |
Vector potential
For the vector field
 , if there exists the vector field
, if there exists the vector field 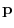 satisfying
satisfying
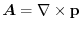
 has vector potential
has vector potential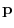 .Here,if the vector field
.Here,if the vector field
 has the vector potential
has the vector potential 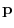 , then by the theorem3.2,
, then by the theorem3.2,
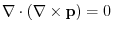 . we have
. we have
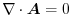 .How about the converse?.
.How about the converse?.
 defined in all space,if
defined in all space,if
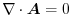 ,then the vector field
,then the vector field
 has a vector potential.
has a vector potential.
To solve the exercise,we introduce a nes symbol. Formal inner product of
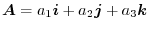 and
and  is an operator such as
is an operator such as
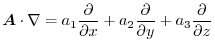
When this is applied to the scalar field  and the vector field
and the vector field
 ,we can write
,we can write
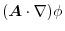 |
 |
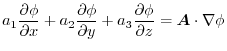 |
|
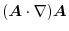 |
 |
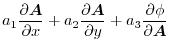 |
The formula
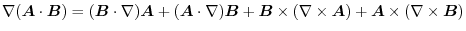
To process an expression containing the operator  ,put
,put  as
as
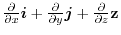 . Then excute
. Then excute  . After that, processing is performed using the scalar triple product and vector triple product learned in vector algebra.
. After that, processing is performed using the scalar triple product and vector triple product learned in vector algebra.
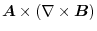 |
 |
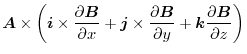 |
|
 |
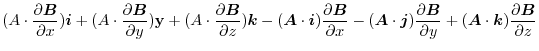 |
 and
and
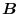 . Then
. Then
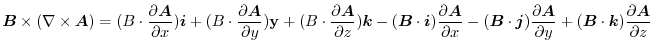
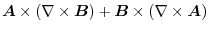 |
|||
 |
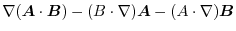 |
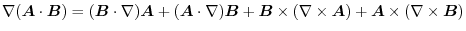
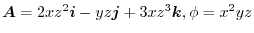 .Find the followings..
.Find the followings..
 so that
so that
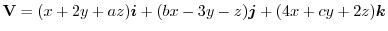 satisfies
satisfies
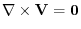 .
.
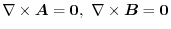 ,then prove that
,then prove that
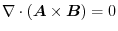 .
.
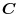 be a constant vector.Then prove the following equation for arbitray vecot field
be a constant vector.Then prove the following equation for arbitray vecot field
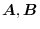 .
.
 , prove the following.
, prove the following.
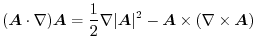
 and
and 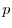 be scalar fields.If
be scalar fields.If
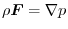 ,then prove that
,then prove that
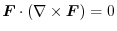 .
.