Next: Rotation Up: Scalar field, vector field Previous: Surface integral Contents Index
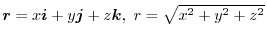 . Then
. Then
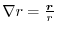
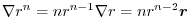
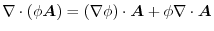
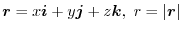 .Find the following scalar.
.Find the following scalar.
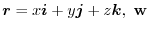 be a constant vector. Then show that .
be a constant vector. Then show that .
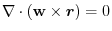
 , prove the followings.
(1)
, prove the followings.
(1)
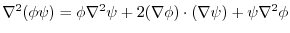
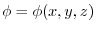 which satisfies
which satisfies
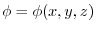
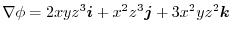 .provided
.provided
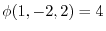 .
.
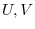 , show the following.
, show the following.
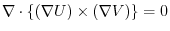
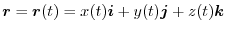 and the scalar field
and the scalar field
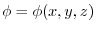 ,show that the derivative
,show that the derivative
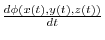 of
of 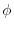 along the curve is equal to
along the curve is equal to
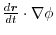 .
.
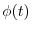 which is composed by putting
which is composed by putting
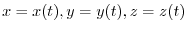 into
into
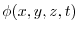 is
is
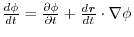 .provided,
.provided,
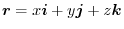 .
.
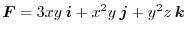 .
.
10. For
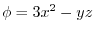 ,
,
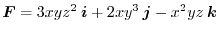 ,find the following scalar.
,find the following scalar.
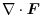
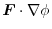
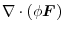
11.
Let
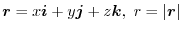 .Prove the following:
.Prove the following:
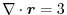 ,
,
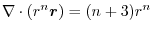
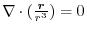
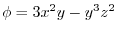 のとき,
のとき,
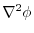 .
.