Rotation

Exercise3.6

1.

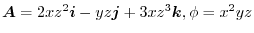Let $\boldsymbol{A} = 2xz^2 \boldsymbol{i} - yz\boldsymbol{j} + 3xz^3\boldsymbol{k}, \phi = x^2 yz$．Find the followings.．

(1)

$\nabla \times \boldsymbol{A}$

(2)

$\nabla \times (\phi \boldsymbol{A})$

(3)

$\nabla \times (\nabla \times \boldsymbol{A})$

2.

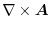
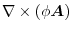
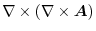
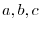Find $a,b,c$ so that 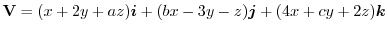$${{\bf V} = (x + 2y + az)\boldsymbol{i} + (bx - 3y -z)\boldsymbol{j} + (4x + cy + 2z)\boldsymbol{k}}$$ satisfies $\nabla \times {\bf V} = {\bf0}$.

3.

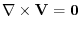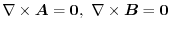If $\nabla \times \boldsymbol{A} = {\bf0},\ \nabla \times \boldsymbol{B} = {\bf0}$，then prove that $\nabla \cdot(\boldsymbol{A} \times \boldsymbol{B}) = 0$．

4.

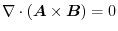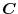Let $\boldsymbol{C}$ be a constant vector．Then prove the following equation for arbitray vecot field $\boldsymbol{A}, \boldsymbol{B}$.

(1)

$\nabla(\boldsymbol{C}\cdot\boldsymbol{A}) = (\boldsymbol{C}\cdot\nabla)\boldsymbol{A} + \boldsymbol{C} \times (\nabla \times \boldsymbol{A})$

(2)

$\nabla \cdot(\boldsymbol{C} \times \boldsymbol{A}) = -\boldsymbol{C} \cdot(\nabla \times \boldsymbol{A})$

(3)

$\nabla \times (\boldsymbol{C} \times \boldsymbol{A}) = \boldsymbol{C} (\nabla \cdot\boldsymbol{A}) - (\boldsymbol{C} \cdot\nabla)\boldsymbol{A}$

5.

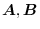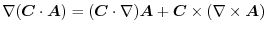
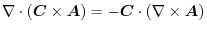
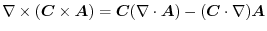
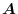For an arbitrary vector field $\boldsymbol{A}$, prove the following．

$$(\boldsymbol{A}\cdot\nabla)\boldsymbol{A} = \frac{1}{2}\nabla \vert\boldsymbol{A}\vert^2 - \boldsymbol{A} \times (\nabla \times \boldsymbol{A})$$

6.

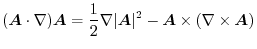
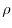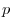Let $\rho$ and $p$ be scalar fields．If 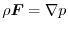$\rho \boldsymbol{F} = \nabla p$，then prove that $\boldsymbol{F}\cdot(\nabla \times \boldsymbol{F}) = 0$．

7.

Find the curl of $${\boldsymbol{F} = z\:\boldsymbol{i} + x^2\:\boldsymbol{j} + 2y\:\boldsymbol{k}}$$

8.

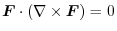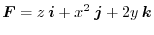
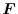If $\boldsymbol{F}$ is conservative， show that $${\nabla \times \boldsymbol{F} = {\bf0}}$$．

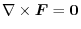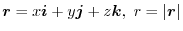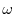9. Let $\boldsymbol{r} = x\boldsymbol{i} + y\boldsymbol{j} + z\boldsymbol{k},\ r = \vert\boldsymbol{r}\vert$ and ${\bf\omega}$ be a constant vector, prove the followings.．

(1)

$$\nabla \times \boldsymbol{r} = {\bf0}\hskip 1cm (2)\ \nabla \times ({\bf\omega} \times \boldsymbol{r}) = 2{\bf\omega}$$

(2)

$\nabla \times \boldsymbol{r} = \left\vert\begin{array}{ccc} \boldsymbol{i} & \b... ...\partial y}{\partial y} - \frac{\partial x}{\partial y})\boldsymbol{k} = {\bf0}$

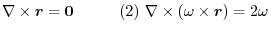
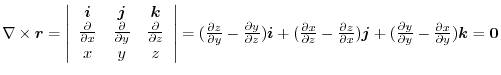
10. Find 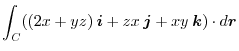$${\int_{C}((2x+yz)\:\boldsymbol{i} + zx\:\boldsymbol{j} + xy\:\boldsymbol{k}) \cdot d\boldsymbol{r}}$$. for

(1)

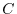$C$ is a close curve

(2)

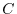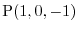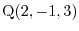$C$ is a curve connecting from the point ${\rm P}(1,0,-1)$ to the point ${\rm Q}(2,-1,3)$.