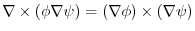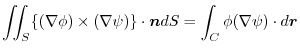Next: Index Up: Introduction to Exercises in Previous: Stokes'theorem Contents Index
 |
 |
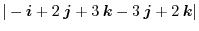 |
|
 |
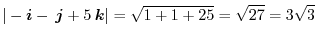 |
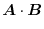 |
 |
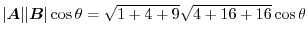 |
|
 |
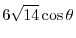 |
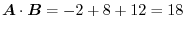 . Thus,
. Thus,
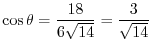
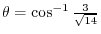 .
.
Exercise Answer1.2
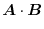 |
 |
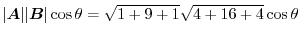 |
|
 |
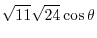 |
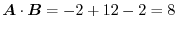 . Thus,
. Thus,
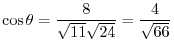
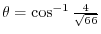 .
.
(2) The unit vector 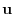 with the direction of
with the direction of
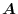 is
is
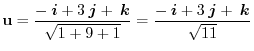
Exercise Answer1.3
![$\displaystyle {}^t[1\ 2\ 1] \times {}^t[2\ -1\ -2]$](img295.png) |
 |
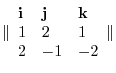 |
|
 |
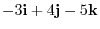 |
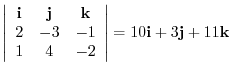
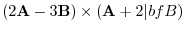 |
 |
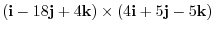 |
|
 |
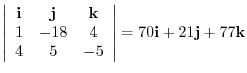 |
(1) The area of parallelogram is
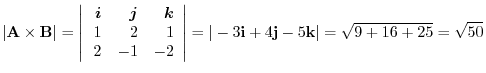
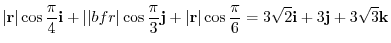
Exercise Answer1.5
1.
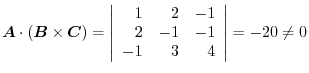 .Thus they are not coplanar.
.Thus they are not coplanar.
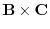 |
 |
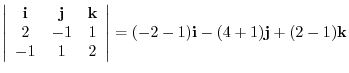 |
|
 |
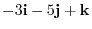 |
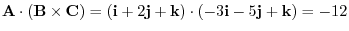
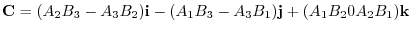
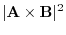 |
 |
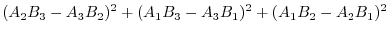 |
|
 |
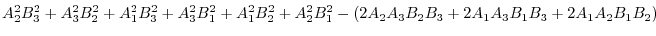 |
||
 |
 |
||
 |
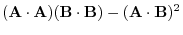 |
Exercise Answer2.1
1. The components of
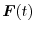 are
are
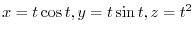 . Then
. Then
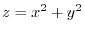 and the trace of
and the trace of
 ,
,
 is on the paraboloid
is on the paraboloid
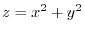 .
.
2. Differentiate eachcomponents, we have
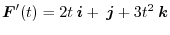
3.
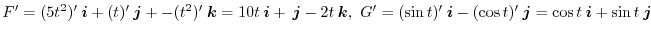 .
.
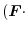 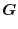 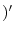 |
 |
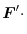 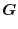 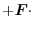 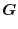  |
|
 |
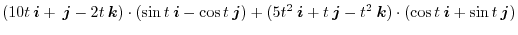 |
||
 |
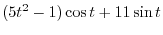 |
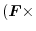 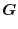 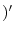 |
 |
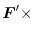 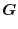 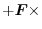 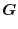  |
|
 |
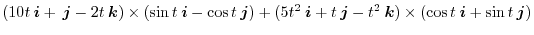 |
||
 |
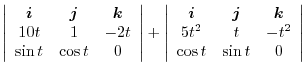 |
||
 |
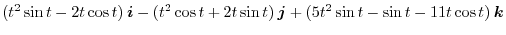 |
4. Let
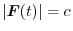 . Then
. Then
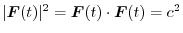 .
Thus, by the derivative of the vector function, we have
.
Thus, by the derivative of the vector function, we have
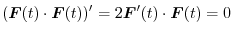
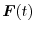 and
and
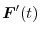 are orthogonal.
are orthogonal.
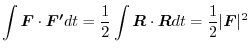
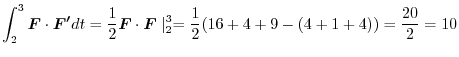
Exercise Answer2.2
1. The straight line to be found has a starting point of 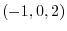 and a direction of
and a direction of
![${}^t [1,4,3]-{}^t [-1,0,2] = {}^t [2,4,1]$](img345.png) . Let the arbitrary point on the line as
. Let the arbitrary point on the line as 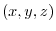 . Then,
. Then,
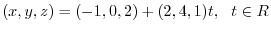
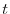 , we have
, we have
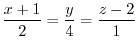
3. The straight line to be found has a starting point of 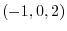 and a direction of
and a direction of
![${}^t [1,4,3]-{}^t [-1,0,2] = {}^t [2,4,1]$](img345.png) . Let the arbitrary point on the line as
. Let the arbitrary point on the line as 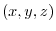 . Then,
. Then,
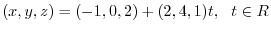
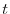 , we have
, we have
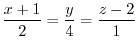
4. Since
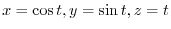 ,we have
,we have
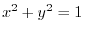 . Thus,
. Thus,
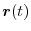 is a smooth curve that spirally rotates around a cylinder with a radius of 1.
is a smooth curve that spirally rotates around a cylinder with a radius of 1.
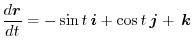
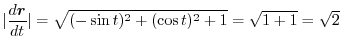
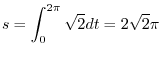
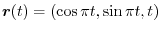
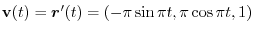
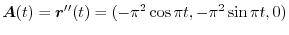
 ,
,
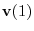 |
 |
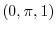 |
|
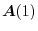 |
 |
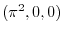 |
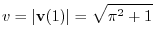
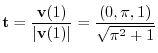
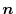 .
Here we will consider a method that is easy to calculate.
.
Here we will consider a method that is easy to calculate.
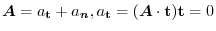
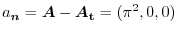
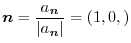
Other way is
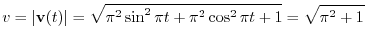
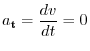
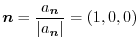
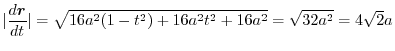
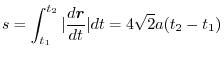
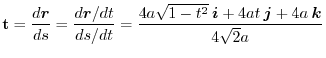
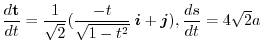 implies
implies
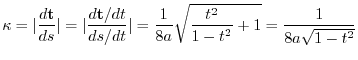
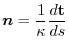 implies
implies
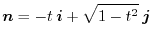
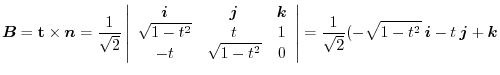
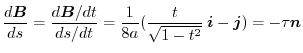
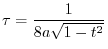
Exercise Answer3.1
1. Let the level surface through the point
 be
be
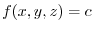
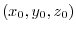 on this level surface be
on this level surface be
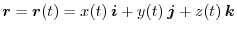
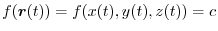 . Thus differentiate both sides by
. Thus differentiate both sides by 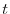 .
.
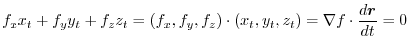
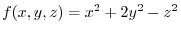
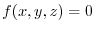 . Also, ,
the normal vector is given by
. Also, ,
the normal vector is given by 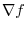 . Thus
. Thus
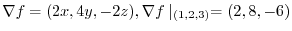
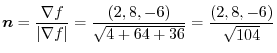
Next, find the directional unit vector to find the directional derivative in the 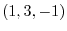 direction at the point
direction at the point 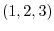 .
.
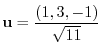 .Then the directional derivative is
.Then the directional derivative is
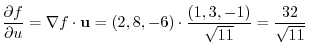
Also, the equation of the tangent plane is
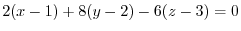 that is
that is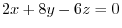
3. Let
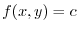 be a streamline equation. Then
be a streamline equation. Then
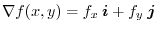 expresses the normal vector of
expresses the normal vector of
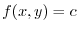 .
.
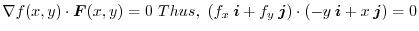
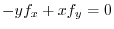 .Note that the slope of the tangent line of
.Note that the slope of the tangent line of
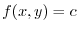 is
is
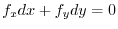 implies
implies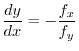
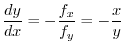
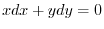 .Thus
.Thus
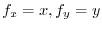 and
Next differentiate the equation 5.1 with respect to
and
Next differentiate the equation 5.1 with respect to 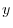 . Then
. Then
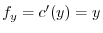 implies
implies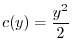
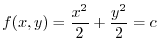
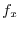 |
 |
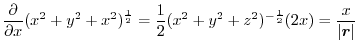 |
|
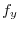 |
 |
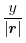 |
|
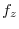 |
 |
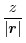 |
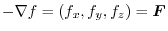 .
Thus,
.
Thus,
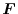 is a conservative field.
is a conservative field.
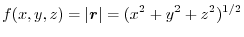
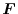 .
.
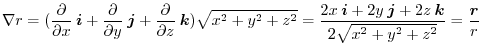
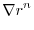 |
 |
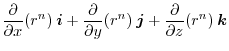 |
|
 |
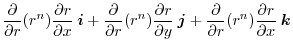 |
||
 |
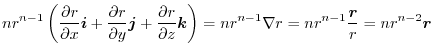 |
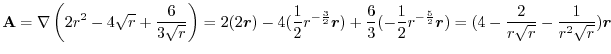
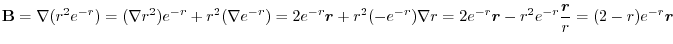
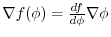 , we have
, we have
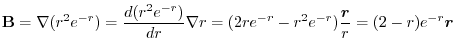
7. Note that
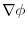 of
of
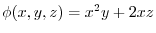 is orthogonal to
is orthogonal to
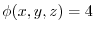 .Therefore the unit normal vector
.Therefore the unit normal vector
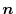 is
is
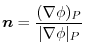
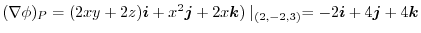 implies
implies
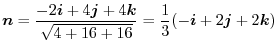
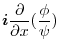 |
 |
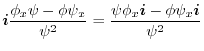 |
|
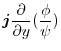 |
 |
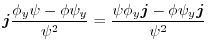 |
|
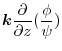 |
 |
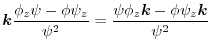 |
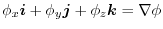 ,
,
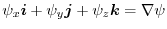 . Thus,
. Thus,
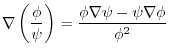
Exercise Answer3.2
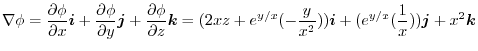
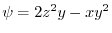 implies,
implies,
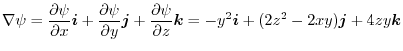
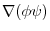 |
 |
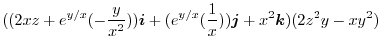 |
|
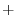 |
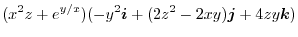 |
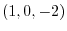 is
is
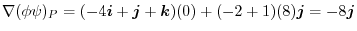
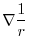 |
 |
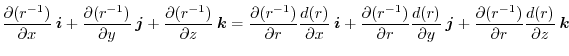 |
|
 |
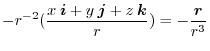 |
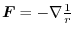 and the vector field
and the vector field
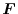 has a potential
has a potential
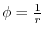 . Therefore, the potential energy at P is
. Therefore, the potential energy at P is
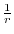 .
.
3. Use
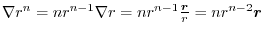
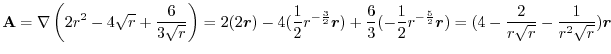
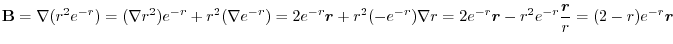
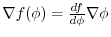 , we have
, we have
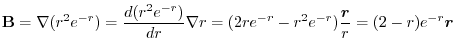
4. Note that
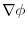 of
of
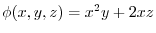 is orthogonal to
is orthogonal to
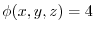 .Therefore the unit normal vector
.Therefore the unit normal vector
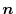 is
is
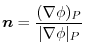
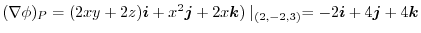 implies
implies
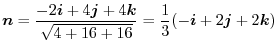
 |
 |
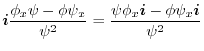 |
|
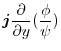 |
 |
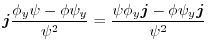 |
|
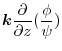 |
 |
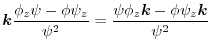 |
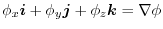 ,
,
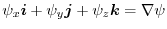 . Thus,
. Thus,
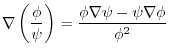
6.
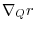 |
 |
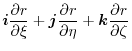 |
|
 |
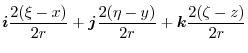 |
||
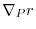 |
 |
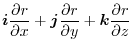 |
|
 |
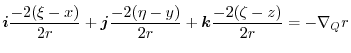 |
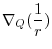 |
 |
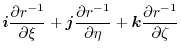 |
|
 |
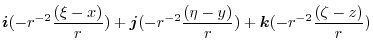 |
||
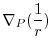 |
 |
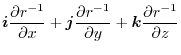 |
|
 |
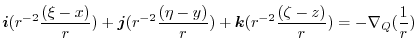 |
Exercise Answer3.3
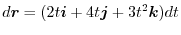
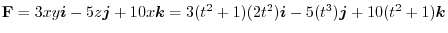 .
Therefore,
.
Therefore,
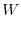 |
 |
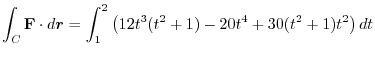 |
|
 |
![$\displaystyle \int_{1}^{2} (12t^5 + 10t^4 + 12t^3 + 30t^2 )dt = \left[2t^6 + 2t^5 + 3t^4 + 10t^3\right]_{1}^{2}$](img477.png) |
||
 |
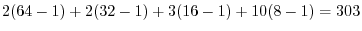 |
2.
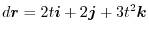
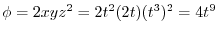 .Therefore,
.Therefore,
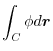 |
 |
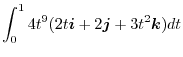 |
|
 |
![$\displaystyle \int_{0}^{1}(8t^{10}\boldsymbol{i} + 8t^{9}\boldsymbol{j} + 12t^{...
...bol{i} + \frac{8}{10}t^{10}\boldsymbol{j} + t^{12}\boldsymbol{k}\right]_{0}^{1}$](img484.png) |
||
 |
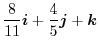 |
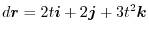
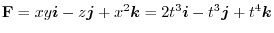 .Therefore,
.Therefore,
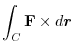 |
 |
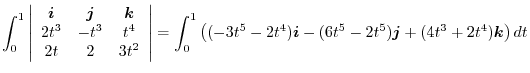 |
|
 |
![$\displaystyle \left[(-\frac{t^6}{2} - \frac{2t^5}{5})\boldsymbol{i} - \frac{4t^6}{6}\boldsymbol{j} + (t^4 + \frac{2t^5}{5})\boldsymbol{k}\right]_{0}^{1}$](img489.png) |
||
 |
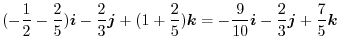 |
3. Note that if 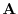 satisfies
satisfies
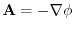 ,then
,then 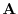 has a scalar potential and
has a scalar potential and
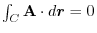 . Thus we find
. Thus we find 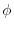 so that,
so that,
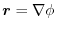 .
.
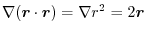
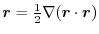 .Therefore,
.Therefore,
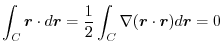
4. The force field
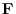 has a potential
has a potential 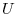 . Then
. Then
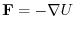 .This suggest that the equation of motion of this mass point is
.This suggest that the equation of motion of this mass point is
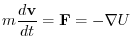
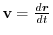 .Then
.Then
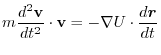
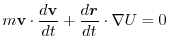
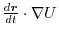 .
.
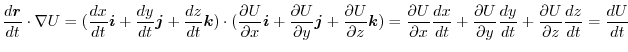
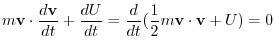
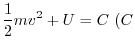 constant
constant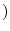
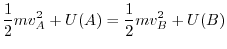
5.
If the origin O is centered on this 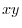 plane and the circle with radius
plane and the circle with radius 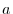 is
is 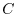 , the equation of motion of the mass point is parametrized by
, the equation of motion of the mass point is parametrized by
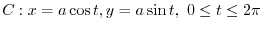 .Thus,
.Thus,
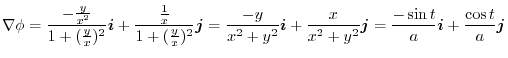
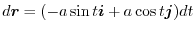
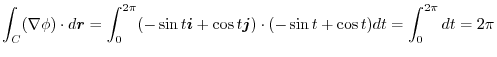
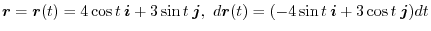
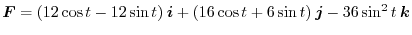
![$\displaystyle \int_{C} \boldsymbol{F} \cdot d \boldsymbol{r} = \int_{0}^{2\pi} [48 - 30\sin{t}\cos{t}]dt = 96\pi$](img514.png)
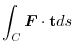 |
 |
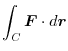 |
|
 |
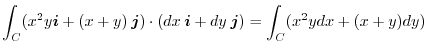 |
||
 |
![$\displaystyle \int_{0}^{2} x^2 x^2 dx + \int_{0}^{2}(x + x^2)(2xdx) = \left[\fr...
...} + \left[\frac{2}{3}x^{3} + \frac{2}{4}x^{4} \right ]_{0}^{2} = \frac{296}{15}$](img518.png) |
8. The directional derivative of 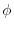 at P
at P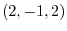 in the direction of
in the direction of 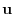 is,
is,
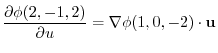
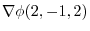 |
 |
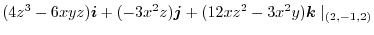 |
|
 |
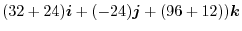 |
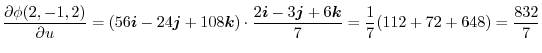
Exercise Answer3.4
1.
(1) When the curved surface  is projected onto the
is projected onto the 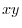 plane,
plane, maps to
maps to
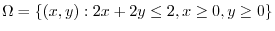 . Also,from the surface
. Also,from the surface
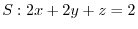 , if the corresponding
, if the corresponding
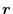 is the position vector,
is the position vector,
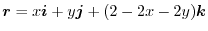
 which is
which is
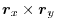 ,
,
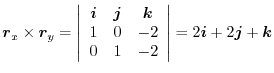
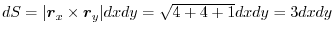 . Then
. Then
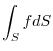 |
 |
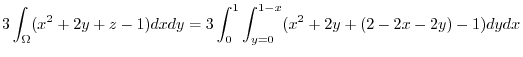 |
|
 |
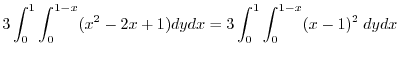 |
||
 |
![$\displaystyle 3\int_{0}^{1}\left[(x-1)^2y\right]_{0}^{1-x}dx = 3\int_{0}^{1}(1-x)^3\;dx = -3\left[\frac{1}{4}(1-x)^{4}\right]_{0}^{1} = \frac{3}{4}$](img534.png) |
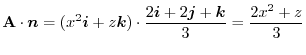
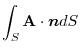 |
 |
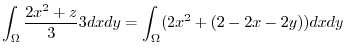 |
|
 |
![$\displaystyle \int_{0}^{1}\int_{0}^{1-x}(2x^2 - 2x - 2y + 2)dy dx = \int_{0}^{1}\left[2x^2 y - 2xy -y^2 + 2y\right]_{0}^{1-x}dx$](img540.png) |
||
 |
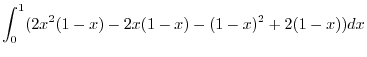 |
||
 |
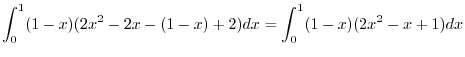 |
||
 |
![$\displaystyle \int_{0}^{1}(-2x^3 +3x^2 - 2x + 1)dx = \left[-\frac{x^4}{2} + x^3 - x^2 + x\right]_{0}^{1}$](img543.png) |
||
 |
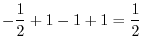 |
2. Since the surface  is region on the
is region on the 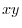 plane,the unit normal vector is
plane,the unit normal vector is
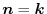 .
.
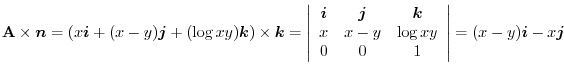
 is on the
is on the 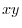 plane. Then
plane. Then
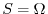 ,
,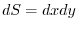 .Here,
.Here,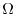 is a disk, so we use the polar coordinates, then
is a disk, so we use the polar coordinates, then
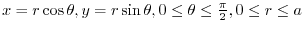 and
and
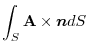 |
 |
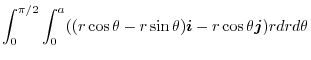 |
|
 |
![$\displaystyle \int_{0}^{\pi/2}\left[\frac{r^3}{3}\right]_{0}^{a}\left((\cos{\theta} - \sin{\theta})\boldsymbol{i} - \cos{\theta}\boldsymbol{j}\right)d\theta$](img553.png) |
||
 |
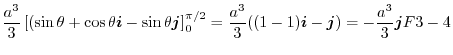 |
3. By projecting  onto
onto 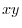 plane, then
plane, then  aps to
aps to
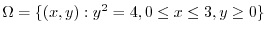 .
Next by letting
.
Next by letting 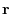 be a position vector
be a position vector
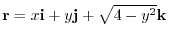 .
Thus,the normal vector of the surface
.
Thus,the normal vector of the surface  is
is
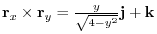 .
Therefore,,
.
Therefore,,
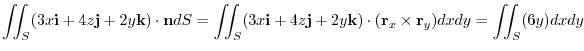
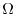 using vertical simple, we have,
using vertical simple, we have,
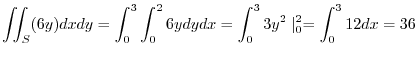
4. By projecting the surface  onto
onto 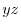 plane,
plane,  maps to
maps to
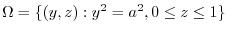 .
Next,let
.
Next,let 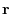 be a postion vector
be a postion vector
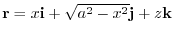 .
Thus,the normal vector of
.
Thus,the normal vector of  is
is
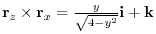 .
.
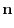 |
 |
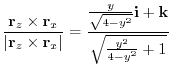 |
|
 |
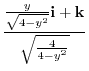 |
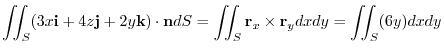
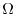 using the vertical simple,
using the vertical simple,
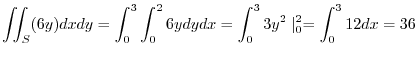
5. The position vector is
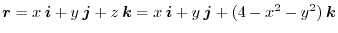 . Then
. Then
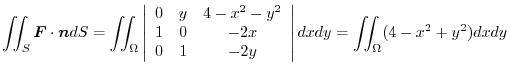
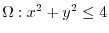 . Then
. Then
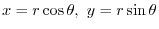 implies
implies
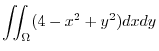 |
 |
![$\displaystyle \int_{0}^{2\pi} \int_{0}^{2}(4 - r^2 + 2r^2 \sin^{2}{\theta})r dr...
...eft[2r^2 - \frac{r^2}{4} + \frac{r^4}{2}\sin^{2}\theta \right ]_{0}^{2} d\theta$](img574.png) |
|
 |
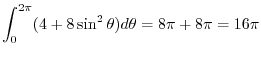 |
6. Let
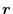 be the position vector corresponds to
be the position vector corresponds to
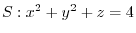 . Then
. Then
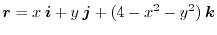
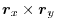 of
of  .
.
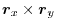 |
 |
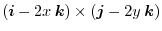 |
|
 |
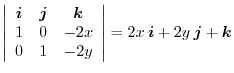 |
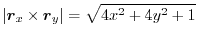
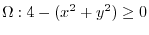 . Then
. Then
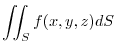 |
 |
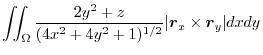 |
|
 |
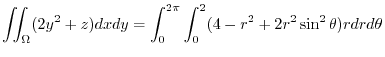 |
||
 |
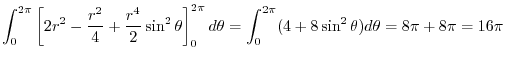 |
8. Since
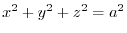 ,for
,for 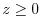 ,the position vector is
,the position vector is
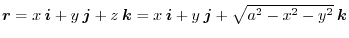 . Thus,
. Thus,
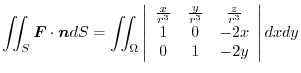
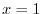 , the position vector is
, the position vector is
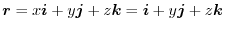 . Here the positive direction is from the bck of the plane to the front of DEFG. Thus, the unit normal vector is
. Here the positive direction is from the bck of the plane to the front of DEFG. Thus, the unit normal vector is
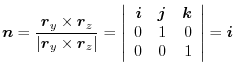
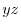 plane is
plane is
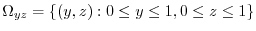 . Then,
. Then,
![$\displaystyle \iint_{DEFG}\boldsymbol{F}\cdot\boldsymbol{n}dS = \int_{0}^{1}\in...
...;dz = \int_{0}^{1}(2-z)dx = \left[2z - \frac{z^2}{2}\right]_{0}^1 = \frac{3}{2}$](img594.png)
For the plane ABCO: since 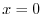 , the position vector is
, the position vector is
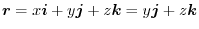 . Here,the positive direction is the direction of the back of plane ABCO to the front.Thus,the unit normal vector is
. Here,the positive direction is the direction of the back of plane ABCO to the front.Thus,the unit normal vector is
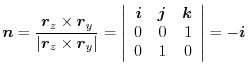
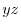 plane is
plane is
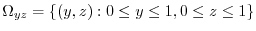 . Then
. Then
![$\displaystyle \iint_{ABCO}\boldsymbol{F}\cdot\boldsymbol{n}dS = \int_{0}^{1}\in...
...y=0}^{1}\;dz = \int_{0}^{1}zdx = \left[\frac{z^2}{2}\right]_{0}^1 = \frac{1}{2}$](img598.png)
For the plane ABEF: since 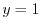 , the position vector is
, the position vector is
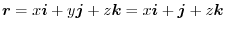 . Here the positive direction is the direction of the back of the plane ABEF to the front. Thus, the unit normla vector is
. Here the positive direction is the direction of the back of the plane ABEF to the front. Thus, the unit normla vector is
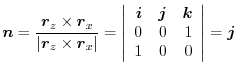
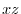 plane is
plane is
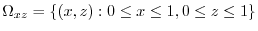 . Then
. Then
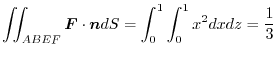
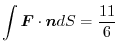
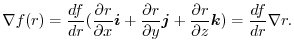
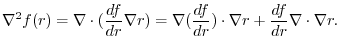
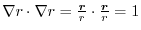 . Also,
. Also,
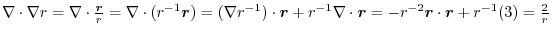 . Therefore,
. Therefore,
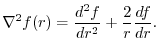
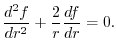
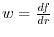 ,then
,then
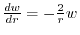 and it is separable.Thus,
and it is separable.Thus,
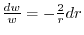 and integrate both sides, we have
and integrate both sides, we have
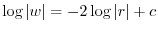 . Thus,
. Thus,
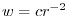 .
.
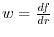 and
and
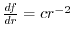 .Therefore,
.Therefore,
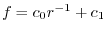 .
Exercise Answer3.5
Basic formula Let
.
Exercise Answer3.5
Basic formula Let
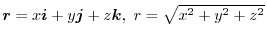 . Then (1)
. Then (1)
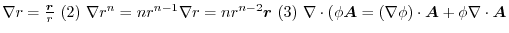
1.
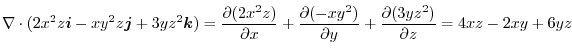
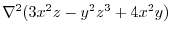 |
 |
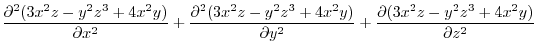 |
|
 |
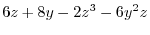 |
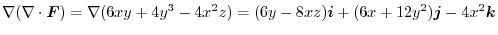
2.
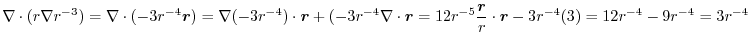
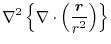 |
 |
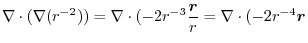 |
|
 |
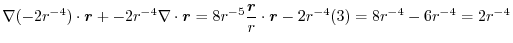 |
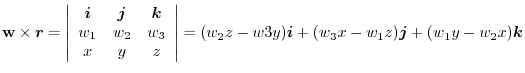
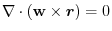
4.
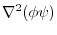 |
 |
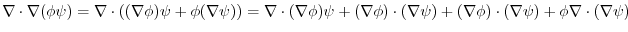 |
|
 |
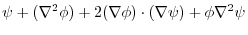 |
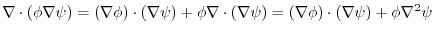 |
(3) (2) implies,
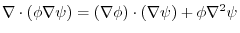 . By symmetry
. By symmetry
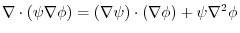 . Therefore,
. Therefore,
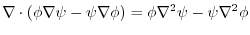 |
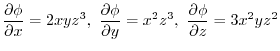
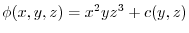 .Here using
.Here using
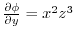 ,
,
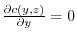 . Then
. Then
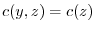 .Finally,
.Finally,
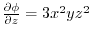 implies
implies
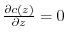 . Then
. Then 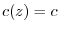 .Thus,
.Thus,
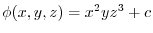 . Now by the initial value
. Now by the initial value
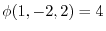 , we have
, we have 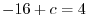 and
and 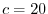 .
.
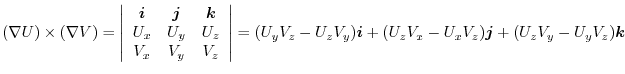
 |
 |
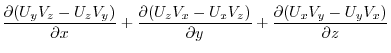 |
|
 |
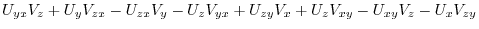 |
||
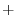 |
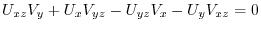 |
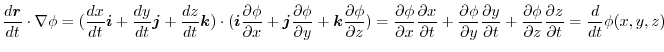
8. Differentiation of composite function implies
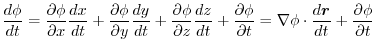
 |
 |
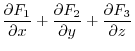 |
|
 |
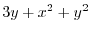 |
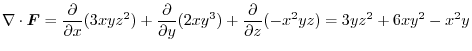
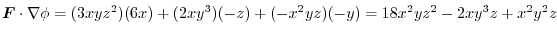
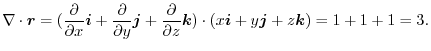
(2) By the differentiation of composite functions,,
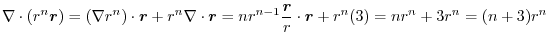
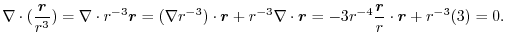
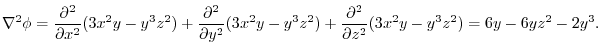
Exercise Answer3.6
1.
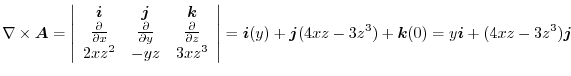
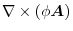 |
 |
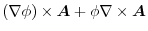 |
|
 |
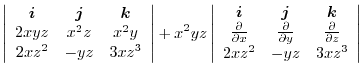 |
||
 |
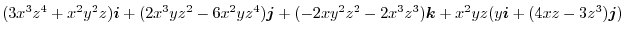 |
||
 |
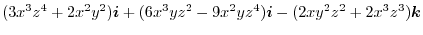 |
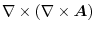 |
 |
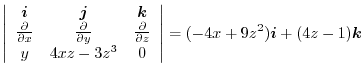 |
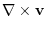 |
 |
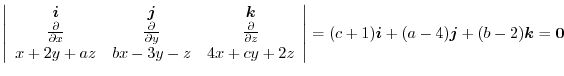 |
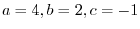
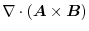 |
 |
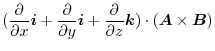 |
|
 |
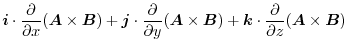 |
||
 |
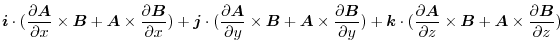 |
||
 |
![$\displaystyle \boldsymbol{B}\cdot(\boldsymbol{i} \times \frac{\partial \boldsym...
...\frac{\partial \boldsymbol{A}}{\partial z})\ \hskip 1cm ([A\ B\ C] = [C\ A\ B])$](img687.png) |
||
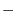 |
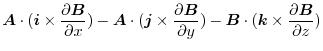 |
||
 |
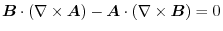 |
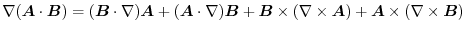
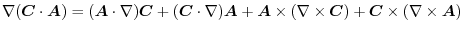
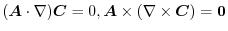 implies
implies
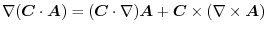
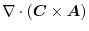 |
 |
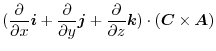 |
|
 |
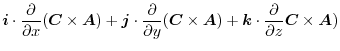 |
||
 |
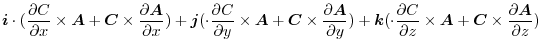 |
||
 |
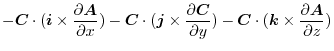 |
||
 |
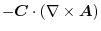 |
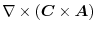 |
 |
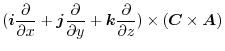 |
|
 |
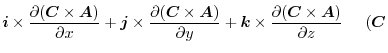 is constant vector) is constant vector)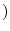 |
||
 |
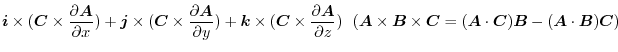 |
||
 |
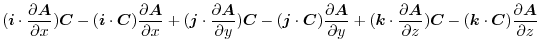 |
||
 |
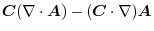 |
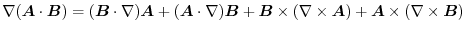
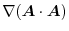 |
 |
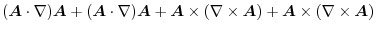 |
|
 |
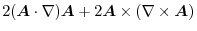 |
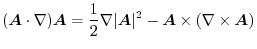
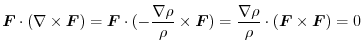
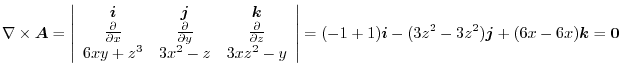
Note that there exits 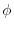 so that
so that
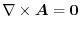 implies
implies
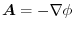 .
.
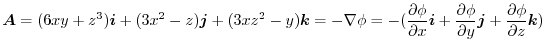
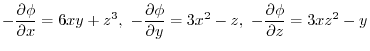
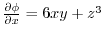 implies
implies
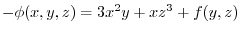 .Now partially differentiate
.Now partially differentiate 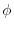 by
by 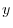 ,
,
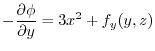
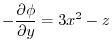
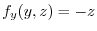
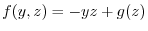 .Thus,
.Thus,
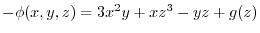 .
Here partially differentiate
.
Here partially differentiate
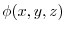 by
by 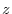 ,
,
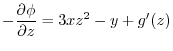
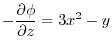
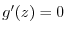
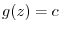 and
and
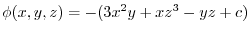
8. Since
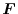 is conservative, there exists
is conservative, there exists 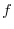 so that
so that
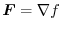 .Now we find
.Now we find
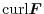 . Then
. Then
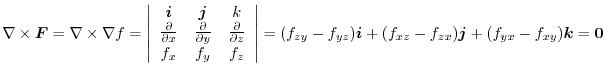
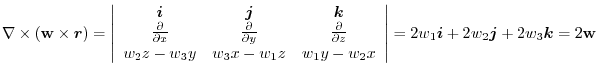
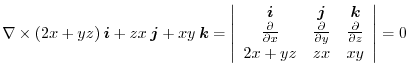
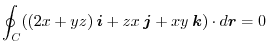
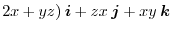 has a scalar potential, we find the scalar potential.
has a scalar potential, we find the scalar potential.
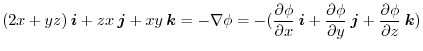
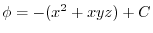 .Note that
.Note that
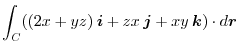 |
 |
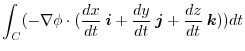 |
|
 |
![$\displaystyle \int_{{\rm P}}^{{\rm Q}}(-d \phi) = -\phi]_{P}^{Q} = (x^2 + xyz)]_{P}^{Q} = 4-6 - 1 = -3$](img745.png) |
Exercise Answer4.1
1.
(1) Gauss's divergence theorem implies
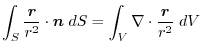
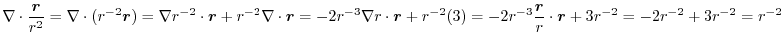
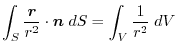
(2) Tranform
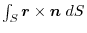 into the surface integral.Using any constant vetor
into the surface integral.Using any constant vetor
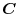 and the triple scalar product,
and the triple scalar product,
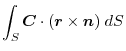 |
 |
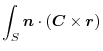 |
|
 |
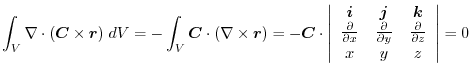 |
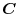 is a constant vector implies
is a constant vector implies
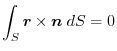
(3) Gauss's dievergence theorem implies
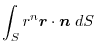 |
 |
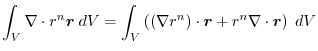 |
|
 |
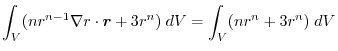 |
||
 |
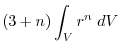 |
(4) Transfrom
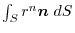 into surface integral.Using a constant vector
into surface integral.Using a constant vector
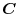 ,
,
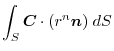 |
 |
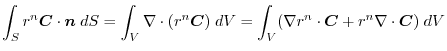 |
|
 |
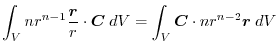 |
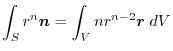
(5) Transform
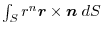 into surface integral.Using a constant vector
into surface integral.Using a constant vector
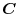 and the triple scalar product,
and the triple scalar product,
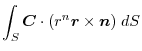 |
 |
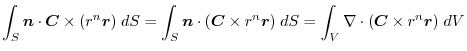 |
|
 |
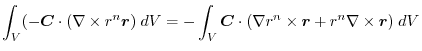 |
||
 |
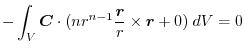 |
(6) Transform
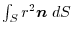 into surface integral.Using a constant vector
into surface integral.Using a constant vector
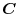 , we have
, we have
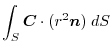 |
 |
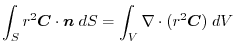 |
|
 |
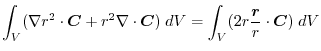 |
||
 |
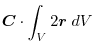 |
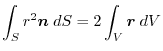
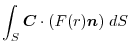 |
 |
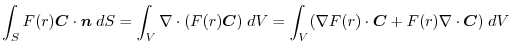 |
|
 |
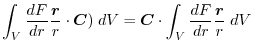 |
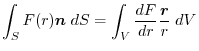
2. Using
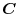 ,we write into surfacee integral.
,we write into surfacee integral.
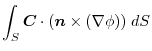 |
 |
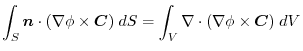 |
|
 |
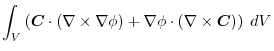 |
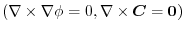 .
.
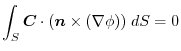
3. Let 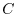 be the boundary of the curved surface
be the boundary of the curved surface  , and let
, and let 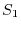 and
and 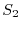 be the curved surfaces separated by the boundary. Also,let the unit normal vector of
be the curved surfaces separated by the boundary. Also,let the unit normal vector of 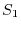 be
be
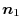 ,the unt normal vector of
,the unt normal vector of 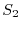 be
be
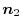 .Then let the unit normal vector of the surface
.Then let the unit normal vector of the surface  be
be
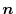 . We have
. We have
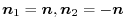 or
or
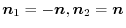 .Here, ,
.Here, ,
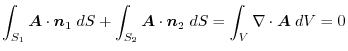
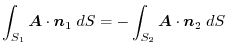
4.
(1) Gauss's divergence theorem implies
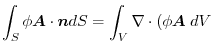
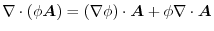 .
.
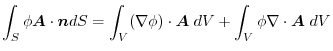
(2) Gauss's divergence theorem implies
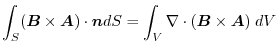
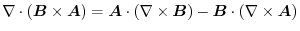 .Thus,
.Thus,
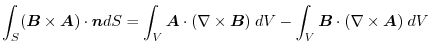
(3) Gauss's divergence theorem implies
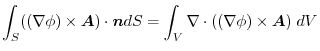
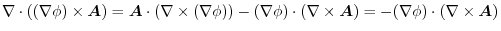
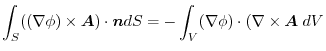
(4) Gauss's divergence theorem implies
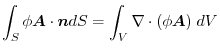
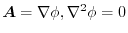 implies
implies
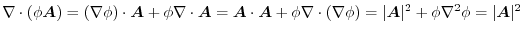
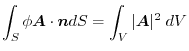
5.
(1)
labelenshu:4-1-5-1
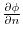 is the directional derivative of the direction of unit normal vector
is the directional derivative of the direction of unit normal vector
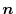 implies
implies
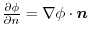 .Thus,
.Thus,
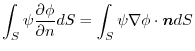
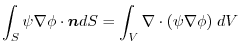
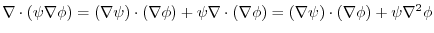 implies
implies
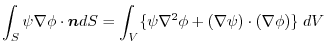
(2)
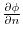 is the directional derivative of the direction of unit normal vector implies
is the directional derivative of the direction of unit normal vector implies
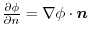 .Thus,
.Thus,
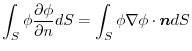
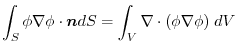
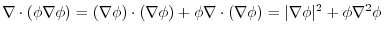 implies
implies
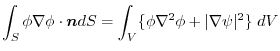
(3) The result of (1) subtracts the result of (2). Then,
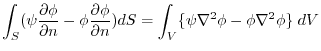
(4)  is harmonic function means that
is harmonic function means that
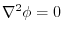 .Therefore,using (2),
.Therefore,using (2),
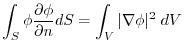
(5)
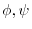 are harmonic functions means that
are harmonic functions means that
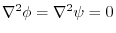 .Therefore,using (3),
.Therefore,using (3),
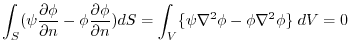
(6) 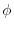 is harmonic function. Then (4)implies
is harmonic function. Then (4)implies
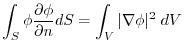
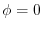 on
on  . Then
. Then
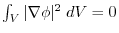 and
and
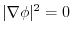 .Thus,
.Thus,
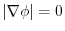 . Hence,
. Hence,
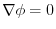 .Therefore,
.Therefore,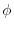 は定数.
は定数.
6. If
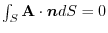 ,then Gauss's divergence theorem implies
,then Gauss's divergence theorem implies
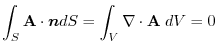
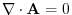 . The theorem 3.4 implies
. The theorem 3.4 implies 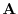 has a vector potential.
has a vector potential.
7.
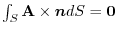 .Here, using a constant vector
.Here, using a constant vector 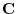 , rewrite into surface integral.
, rewrite into surface integral.
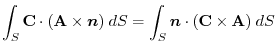
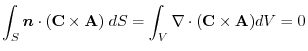
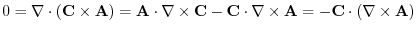
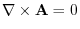 and
and 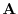 has a scalar potential.
has a scalar potential.
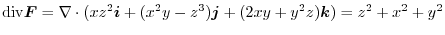
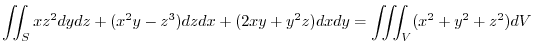
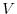 is an upper sphere with the radius
is an upper sphere with the radius 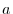 . Then by the spherical coordinate transformation
. Then by the spherical coordinate transformation
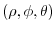 , we have
, we have
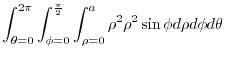 |
 |
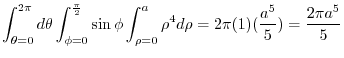 |
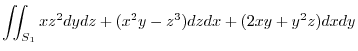 |
 |
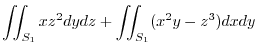 |
|
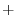 |
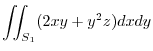 |
Since
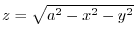 ,projection onto
,projection onto 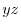 plane,
plane,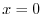 implies
implies
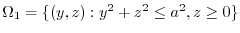 . Here,we consier
. Here,we consier 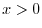 and
and 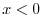 .
.
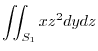 |
 |
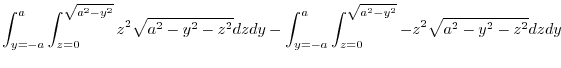 |
|
 |
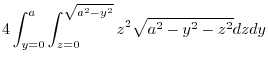 |
Next projection onto 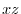 plane. Then
plane. Then 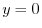 implies
implies
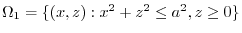 .Thus,for
.Thus,for 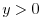 and
and 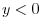 ,
,
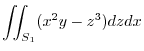 |
 |
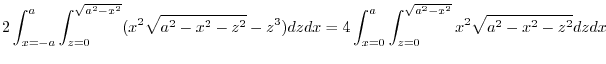 |
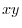 plane. Then
plane. Then 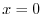 implies
implies
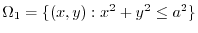 .
.
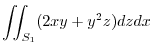 |
 |
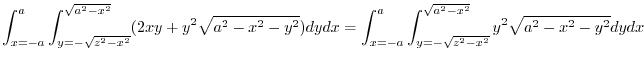 |
|
 |
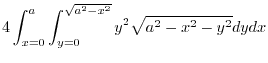 |
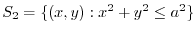 .First projection onto,
.First projection onto,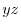 plane.
plane. 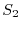 maps to
maps to
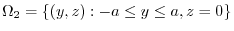 .
.
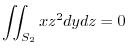
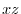 plane,
plane,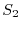 maps to
maps to
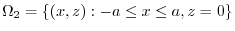 .,
.,
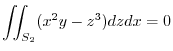
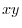 plane,
plane, 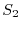 maps to
maps to
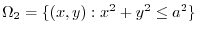 .
.
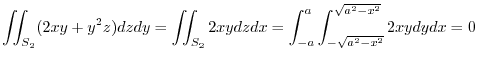
Adding these,
 |
 |
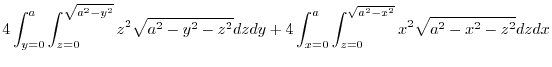 |
|
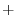 |
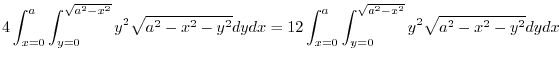 |
Here using the polar coorinates,we have
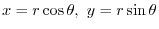 . Thus
. Thus
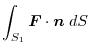 |
 |
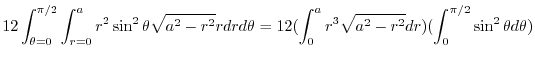 |
|
 |
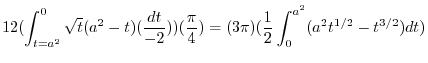 |
||
 |
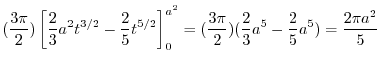 |
(1) Using the arbitrary constant, we express by the surface integral and apply Gauss's divergence theorem. Then
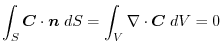
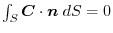
(2) By Gauss's divergence theorem,
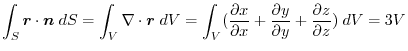
(3) Using a constant vector,we express by the surface integral and apply the triple scalar product and Gauss's divergance theorem,
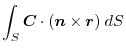 |
 |
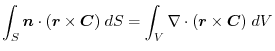 |
|
 |
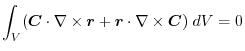 |
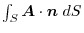 .In this case,
.In this case,
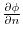 isa directional derivative in the direction of the unit normal vector
isa directional derivative in the direction of the unit normal vector
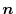 . Then
. Then
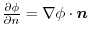 .Therefore,,
.Therefore,,
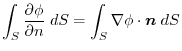
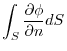 |
 |
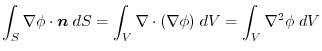 |
(2) 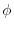 is harmonic function. Then
is harmonic function. Then
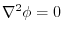 . Thus,(1) implies
. Thus,(1) implies
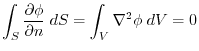
Exercise Answer4.2
1.
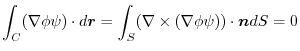
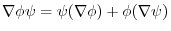
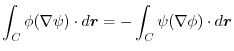
2.
(1) Rewrite a line integral into
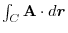 .To do so, using a constant vector
.To do so, using a constant vector 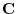 and the triple scalar product,we have
and the triple scalar product,we have
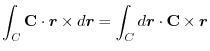
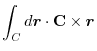 |
 |
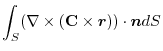 |
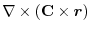 |
 |
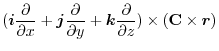 |
|
 |
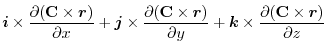 |
||
 |
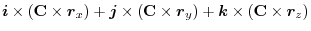 |
||
 |
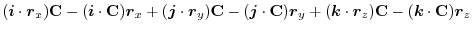 |
||
 |
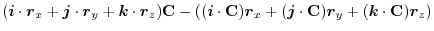 |
||
 |
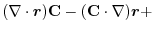 |
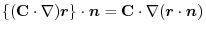
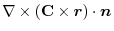 |
 |
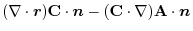 |
|
 |
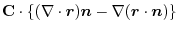 |
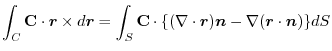
 is a constant vector. Then,
is a constant vector. Then,
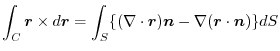
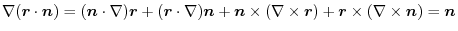
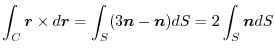
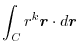 |
 |
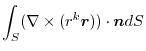 |
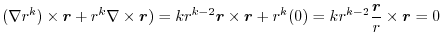
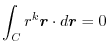
(3) Let 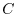 be a constant vector. Then using Stokes' theorem,
be a constant vector. Then using Stokes' theorem,
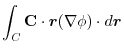 |
 |
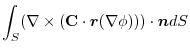 |
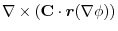 |
 |
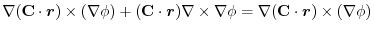 |
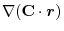 |
 |
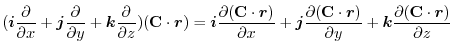 |
|
 |
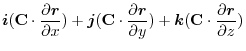 |
||
 |
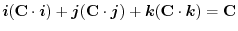 |
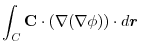 |
 |
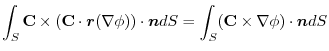 |
|
 |
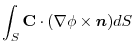 |
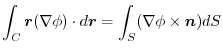
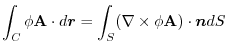
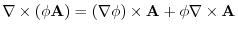
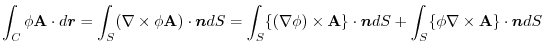
4. Rewrite the line integral into
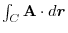 .Then using a constant vector
.Then using a constant vector 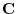 and the triple scalar product,and Stokes' theorem,we have
and the triple scalar product,and Stokes' theorem,we have
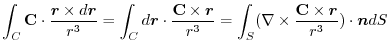
Here using the triple scalar product, we have
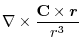 |
 |
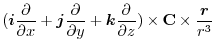 |
|
 |
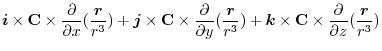 |
||
 |
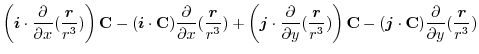 |
||
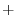 |
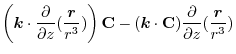 |
||
 |
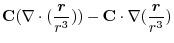 |
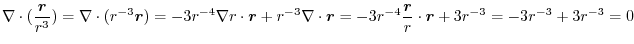
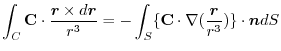
 is a constant vector.
is a constant vector.
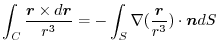
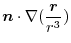 |
 |
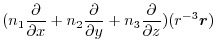 |
|
 |
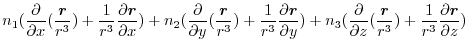 |
||
 |
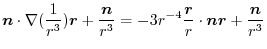 |
||
 |
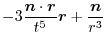 |
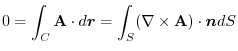
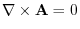 .Therefore,
.Therefore,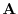 has a scalar potential.
has a scalar potential.
6 The boundary of  ,
,
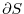 is a circle
is a circle
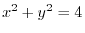 .Thus the position vector is
.Thus the position vector is
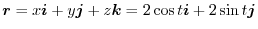 . Then we find the line integral
. Then we find the line integral
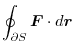 |
 |
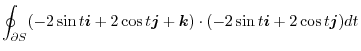 |
|
 |
![$\displaystyle \int_{0}^{2\pi}[4\sin^{2}{t} + 4\cos^{2}{t}]dt = 8\pi$](img942.png) |
Next we find the surface integral..
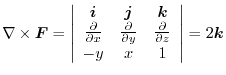
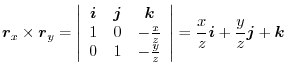
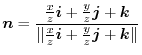
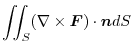 |
 |
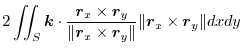 |
|
 |
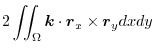 |
||
 |
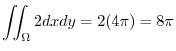 |
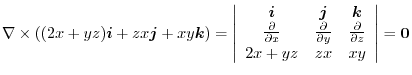
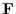 has a scalar potential.So, we find
has a scalar potential.So, we find 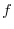 so that
so that
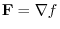 .
.
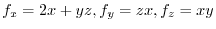 implies
implies
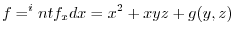
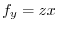 imlies
imlies
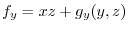 . Thus,
. Thus,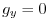 . in other words,
. in other words,
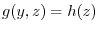 . Next,
. Next,
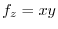 implies
implies
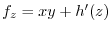 . Thus
. Thus 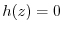 .Here,let
.Here,let 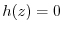 . Then
. Then
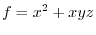
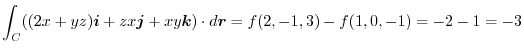
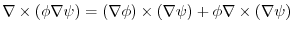
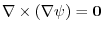 implies
implies