Next: Divergence Up: Scalar field, vector field Previous: Line integral Contents Index
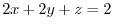 and
and 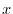 -axis,
-axis,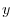 -axis, and
-axis, and 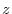 -axis, and the surface
-axis, and the surface 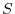 be the
be the 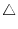 ABC. Find the following surface integrals.
ABC. Find the following surface integrals.
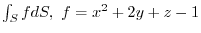
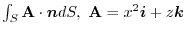
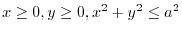 on the
on the 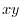 -plane be
-plane be 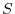 .Find the surface integral.
.Find the surface integral.
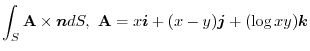
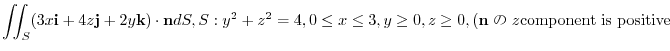
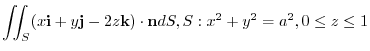
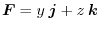 ,surface be
,surface be
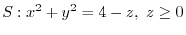 .Find the surface integral of
.Find the surface integral of
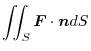
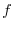 on the paraboloid
on the paraboloid
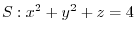 where
where 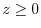 .
.
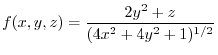
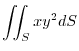 , where
, where
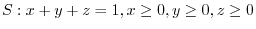 .
.
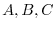 be the intersection of the plane
be the intersection of the plane
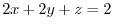 and
and 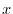 -axis,
-axis,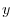 -axis,
-axis, 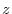 -axis and let the
-axis and let the 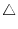 ABC be the surface
ABC be the surface 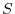 . Find
. Find
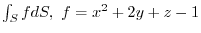 .
.
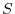 be the sphere of the radius
be the sphere of the radius 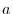 with the center O.Let
with the center O.Let
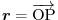 be the position vector of
be the position vector of 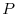 .Then by taking the unit normal vector
.Then by taking the unit normal vector
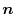 of the sperical surface
of the sperical surface 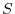 outward, prove the followings.
outward, prove the followings.
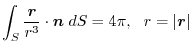
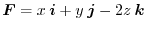 , and the surface be
, and the surface be
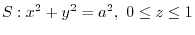 .Then find the surface integral of
.Then find the surface integral of
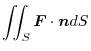 .
.
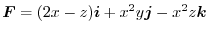 ,Let the surface
,Let the surface 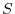 be a bounded part of the plane
be a bounded part of the plane
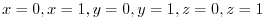 .Then find the surface integral
.Then find the surface integral
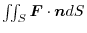 .
.
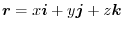 ,
,
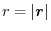 . Find the followings.
. Find the followings.
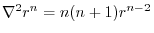
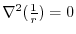
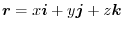 ,
,
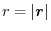 .
.
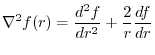 よ.
よ.
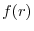 so that
so that
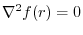 ..
..