Line integral

Exercise3.3

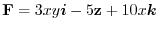Given the force field ${\mathbf F} = 3xy \boldsymbol{i} - 5{\bf z} + 10 x\boldsymbol{k}$ . Find the work done by 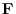${\mathbf F}$ which is 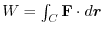$W = \int_{C}{\mathbf F}\cdot d\boldsymbol{r}$ , moving along the curve

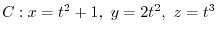
$\displaystyle C : x = t^2 + 1,\ y = 2t^2,\ z = t^3$

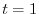from to .

2.

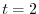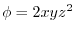Given the scalar field $\phi = 2xyz^2$ ，the field 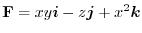${\mathbf F} = xy\boldsymbol{i} - z\boldsymbol{j} + x^2 \boldsymbol{k}$ . Let the curve 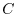be parametrized by 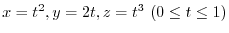$x = t^2, y = 2t, z = t^3\ (0 \leq t \leq 1)$ ．Find the following line integrals.

(1)

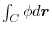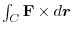
$\int_{C}\phi d\boldsymbol{r}$ (2) $\int_{C}{\mathbf F} \times d\boldsymbol{r}$

3.

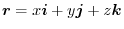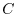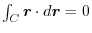Let $\boldsymbol{r} = x\boldsymbol{i} + y\boldsymbol{j} + z \boldsymbol{k}$ ．Then for any closed curve , prove that $\int_{C}\boldsymbol{r}\cdot d\boldsymbol{r} = 0$ ．

4.

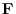Suppose that the force field ${\mathbf F}$ has the potential 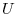．Within the force field, the point mass with the mass 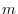moves from the point A to the point B, show that following equation holds．

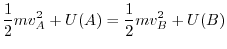
$\displaystyle \frac{1}{2}mv_{A}^2 + U(A) = \frac{1}{2}mv_{B}^2 + U(B)$

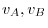Here， $v_{A},v_{B}$ are the magnitude of velocity vectors of A and B.

5.

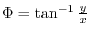$\Phi = \tan^{-1}{\frac{y}{x}}$ is defined in the domain 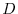excluding the 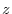axis from the whole space． Let 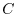be a circle with a radius of 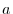centered at the origin O on the 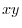plane. Prove the following equation.

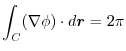
$\displaystyle \int_{C}(\nabla \phi)\cdot d\boldsymbol{r} = 2\pi$

#F#>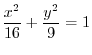ind the amount of work done by the mass point to go around $\displaystyle{\frac{x^2}{16} + \frac{y^2}{9} = 1}$ . Note that vector field is given by

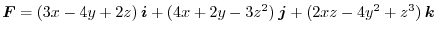
$\displaystyle \boldsymbol{F} = (3x-4y+2z)\:\boldsymbol{i} + (4x+2y-3z^2)\:\boldsymbol{j} + (2xz-4y^2 + z^3)\:\boldsymbol{k}$

7.

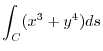Evaluate the line integral $\displaystyle{\int_{C}(x^3 + y^4)ds}$ , where 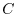is a line connecting the points 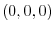and .

8.

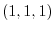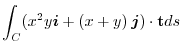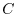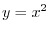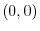Find the line integral $\displaystyle{\int_{C}(x^2 y\boldsymbol{i} + (x+y)\:\boldsymbol{j}) \cdot{\bf t}ds}$ ．Here， is the curve $\displaystyle{y = x^2}$ from to 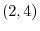.