Next: Line integral Up: Scalar field, vector field Previous: Gradient and directional derivative Contents Index
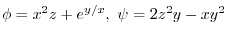 , find the followings:
, find the followings:
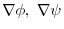
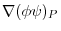 of
of
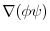 at P
at P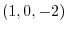 .
.
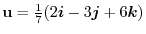 of
of
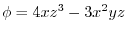 at P
at P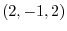 .
.
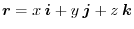 C
C
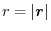 . Then show that the vector field
. Then show that the vector field
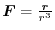 has the scalar potential
has the scalar potential
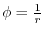 and find the potential energy at each point in space.
and find the potential energy at each point in space.
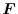 has the potential
has the potential 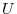 . Prove that the following equation holds when a mass point with mass
. Prove that the following equation holds when a mass point with mass 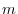 moves in this force field and moves from point A to point B.
moves in this force field and moves from point A to point B.
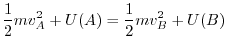
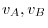 are magnitude of the velocity vectors at
are magnitude of the velocity vectors at 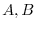 , respectivelyD
, respectivelyD
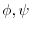 , show the followings.
, show the followings.
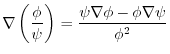
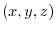 , Q
, Q
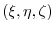 be
be 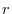 . Then prove the following for the differential operator
. Then prove the following for the differential operator