Next: Vector field Up: Scalar field, vector field Previous: Scalar field, vector field Contents Index
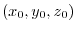 is orthogonal to the level surface through the point
is orthogonal to the level surface through the point
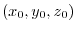 .
.
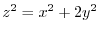 at
at 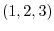 and find the directional derivative in the direction of
and find the directional derivative in the direction of 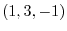 and the equation of tangent plane.
and the equation of tangent plane.
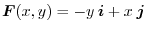 .
.
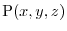 be
be
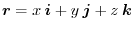 ,and vector field be
,and vector field be
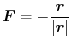 . Then show that this vector field is a conservative field in any area except at origin and
. Then show that this vector field is a conservative field in any area except at origin and
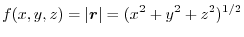
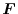 .
.
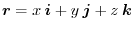 and the scalar field
and the scalar field
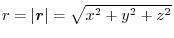 , show the followings:
, show the followings:
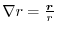
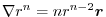
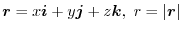 . Then find
. Then find
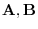 ..
..
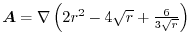
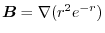
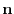 of
of
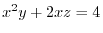 at P
at P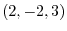 .
.
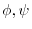 , show the followings.
, show the followings.