Next: Inverse function of elementary Up: Elementary functions Previous: meromorphic function Index
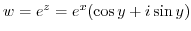 is called an exponential function and expressed as
is called an exponential function and expressed as 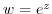 or
or
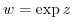 .
.
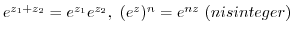
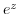 has a period of
has a period of 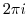 .
.
Proof (1) Let
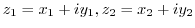 . Then
. Then
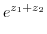 |
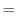 |
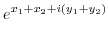 |
|
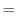 |
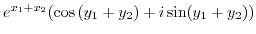 |
||
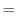 |
![$\displaystyle e^{x_{1} + x_{2}}[\cos{y_{1}}\cos{y_{2}} - \sin{y_{1}}\sin{y_{2}} + i(\sin{y_{1}}\cos{y_{2}} + \cos{y_{1}}\sin{y_{2}})]$](img121.png) |
||
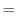 |
![$\displaystyle e^{x_{1} + x_{2}}[(\cos{y_{1}} + i\sin{y_{1}})(\cos{y_{2}}+i\sin{y_{2}})]$](img122.png) |
||
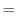 |
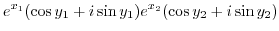 |
||
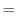 |
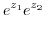 |
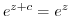 holds, the function
holds, the function 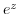 is said to have a period
is said to have a period 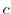 .
Then we let
.
Then we let
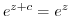 . Since
. Since
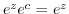 , we have
, we have 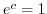 . Let
. Let
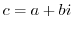 . Then
. Then
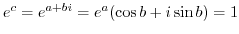 implies
implies
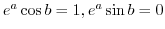 . Thus,
. Thus,
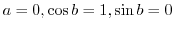 .
. 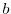 that satisfies this,
that satisfies this,
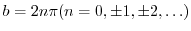 . Therefore,
. Therefore, 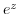 has a period
has a period 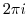 .
.
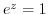
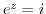
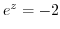
2. Express the following value in the form of 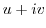 .
.
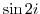
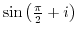
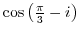
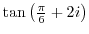
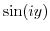
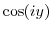
3. Prove the following formulas.
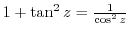
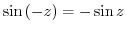
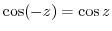
4. Show that for 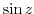 .
.
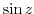 has a period
has a period 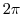
(5) Find the period of 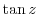 .
.