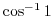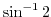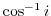Inverse function of elementary function

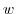Logarithmic function The inverse function of the exponential function of a complex variable is called logarithmic function of the complex variable. That is, between the complex variables $z$ and $w$, there is a relationship so that

$$z = e^{w}$$

we define

$$w = \log{z}$$

However, since the exponential function has a period of $2\pi i$,

$$z = re^{i\theta} = re^{i(\theta + 2k\pi)}$$

and

$$w = \log{z} = \log{r} + i(\theta + 2k\pi)$$

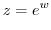
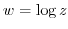
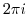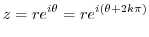
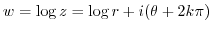
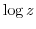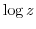Therefore, The logarithmic function $\log{z}$ corresponds to an infinite number of different values ​for one complex number $z$. That is, it is an infinite multivalued function. The principal value or principal brunch of $\log{z}$ is given by

$$\log{z} = \log{z} + i\theta, 0 \leq \theta < 2\pi$$

Exercise2.4

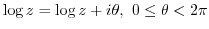
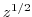1. Show that $z^{1/2}$ has two branches.

2. Find all of the following values.

(a)

$\log{2}$

(b)

$\log{(-1)}$

(c)

$\log{i}$

(d)

$\log(1+i)$

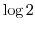
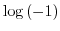
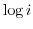
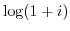
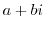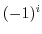
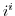
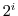
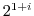
3. Express the following value in the form of $a + bi$.

(a)

$(-1)^{i}$

(b)

$i^{i}$

(c)

$2^{i}$

(d)

$2^{1+i}$

4. Prove the following formulas.

(a)

$\sin^{-1}{z} = \frac{1}{i}\log{(iz \pm \sqrt{1 - z^2})}$

(b)

$\tan^{-1}{z} = \frac{1}{2i}\log{\frac{1 + iz}{1 - iz}}$

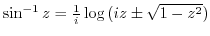
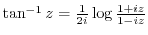
(5) Find the following values.

(a)

$\cos^{-1}{1}$

(b)

$\sin^{-1}{2}$

(c)

$\cos^{-1}{i}$