Next: Limit and continuity Up: Solution Previous: 2.3 Elementary functions Index
1.
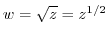 means that
means that
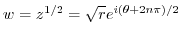 . Thus, it is two-valued function. Now let
. Thus, it is two-valued function. Now let
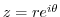 . Then
. Then
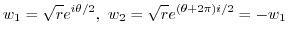
2.
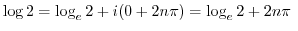
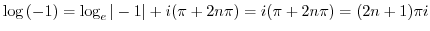
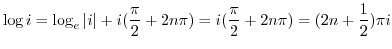
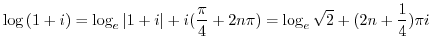
3.
![$\displaystyle (-1)^{i} = e^{i\log{(-1)}} = e^{i [\log_{e}{\vert-1\vert} + i(\pi + 2n\pi)]} = e^{-(2n+1)\pi}$](img646.png)
![$\displaystyle (i)^{i} = e^{i\log{(i)}} = e^{i [\log_{e}{\vert i\vert} + i(\frac{\pi}{2} + 2n\pi)]} = e^{-(2n+\frac{1}{2})\pi}$](img647.png)
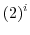 |
 |
![$\displaystyle e^{i\log{(2)}} = e^{i [\log_{e}{\vert 2\vert} + i(0 + 2n\pi)]}$](img649.png) |
|
 |
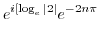 |
||
 |
![$\displaystyle e^{-2n\pi}[\cos{(\log_{e}{2})}+i \sin{(\log_{e}{2})}]$](img651.png) |
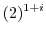 |
 |
![$\displaystyle 2\cdot2^{i} = 2e^{i\log{(2)}} = 2e^{i [\log_{e}{\vert 2\vert} + i(0 + 2n\pi)]}$](img653.png) |
|
 |
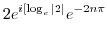 |
||
 |
![$\displaystyle 2e^{-2n\pi}[\cos{(\log_{e}{2})}+i \sin{(\log_{e}{2})}]$](img655.png) |
4.
Let
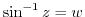 . Then
. Then
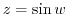 . Note that the complex function
. Note that the complex function 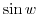 is expressed by the exponential function.
is expressed by the exponential function.
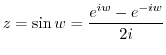
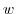 .
.
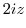 |
 |
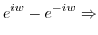 |
|
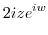 |
 |
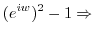 |
|
| 0 |  |
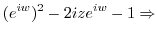 |
|
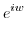 |
 |
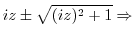 |
|
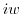 |
 |
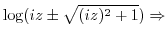 |
|
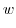 |
 |
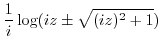 |
Note Assuming that
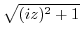 represents two branches with
represents two branches with 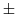 in front of the radical symbol at the same time by divalentity, only
in front of the radical symbol at the same time by divalentity, only 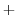 is required.
is required.
Let
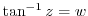 . Then
. Then
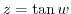 . Note that the complex function
. Note that the complex function 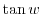 can be represented by exponential function.
can be represented by exponential function.
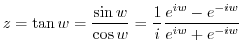
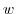 . Then
. Then
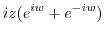 |
 |
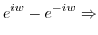 |
|
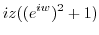 |
 |
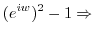 |
|
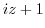 |
 |
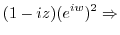 |
|
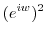 |
 |
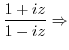 |
|
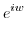 |
 |
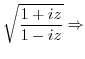 |
|
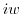 |
 |
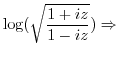 |
|
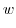 |
 |
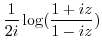 |
5.
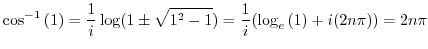
Alternate solution Let
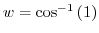 . Then
. Then
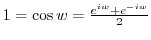 . Solve this for
. Solve this for 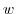 . Then
. Then
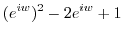 |
 |
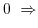 |
|
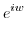 |
 |
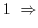 |
|
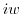 |
 |
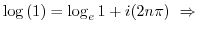 |
|
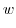 |
 |
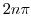 |
Note
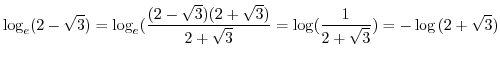
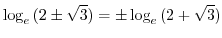
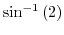 |
 |
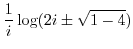 |
|
 |
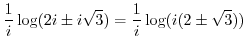 |
||
 |
![$\displaystyle \frac{1}{i}(\log{(i)} + \log{(2 \pm \sqrt{3})}) = \frac{1}{i}[i(2n + \frac{1}{2})\pi + \log_{e}{(2 \pm \sqrt{3})} + i(2n\pi)]$](img701.png) |
||
 |
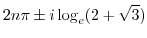 |
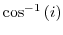 |
 |
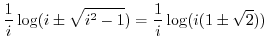 |
|
 |
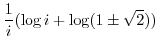 |
Note that
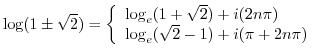
![$\displaystyle \cos^{-1}{(i)} = \left\{\begin{array}{l}
-i[(2n + \frac{1}{2})\pi...
...}) ] \\
-i[(2n + \frac{3}{2})\pi + \log_{e}(\sqrt{2} - 1) ]
\end{array}\right.$](img707.png)