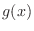Next: Evaluating Definite Integral Up: Integration Previous: Integration of Irrational Functions Contents Index
Understanding Partition the interval ![$[a,b]$](img1050.png) into smaller intervals. Consider the small rectangle with the base equal to the length of an interval and the height equal to the value of function.
into smaller intervals. Consider the small rectangle with the base equal to the length of an interval and the height equal to the value of function.
Definite Integral
Suppose that  is defined on
is defined on ![$[a,b]$](img1050.png) . Partition the interval
. Partition the interval ![$[a,b]$](img1050.png) into
into  smaller intervals. Let
smaller intervals. Let 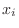 be such that for
be such that for
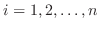
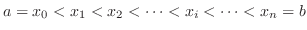
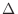 . The norm of the interval is the width of intervals that is
. The norm of the interval is the width of intervals that is
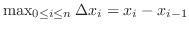 and denoted by
and denoted by 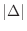 . Now take
. Now take 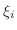 in the subinterval
in the subinterval
![$[x_{i-1},x_{i}]$](img2810.png) and consider the sum called Riemann Sum
and consider the sum called Riemann Sum
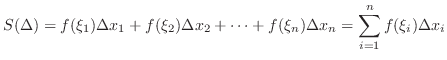
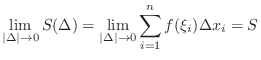
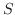 definite integral of
definite integral of  and
and  is called Riemann integrable function on
is called Riemann integrable function on ![$[a,b]$](img1050.png) . We write
. We write 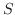 as
as
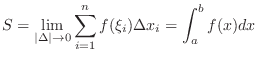
Integrable Functions Note that  is integrable function on
is integrable function on ![$[a,b]$](img1050.png) if and only if the limit of Riemann sum is independent of the choice of partition and choice of
if and only if the limit of Riemann sum is independent of the choice of partition and choice of 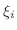 .
.
Integration by Quadrature
Divide ![$[a,b]$](img1050.png) into
into 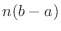 equal parts. Then
equal parts. Then
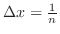 and
and
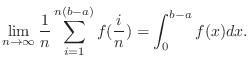
Lower and Upper Limit To find the lower limit of an integral, Set 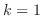 and
and
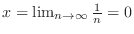 . To find the upper limit of an integral, Set
. To find the upper limit of an integral, Set
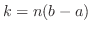 and
and
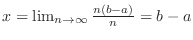 .
.
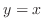 ,
, 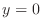 , and
, and 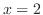 using integration by quadrature.
using integration by quadrature.![$[0,2]$](img2823.png) into
into 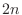 equal subintervals whose length is
equal subintervals whose length is
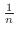 . Then Riemann sum is
. Then Riemann sum is
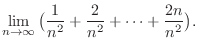
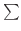 notation, we have
notation, we have
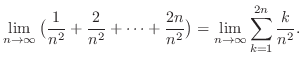
 out of
out of  sign.
sign.
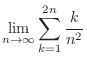 |
 |
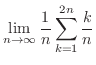 |
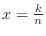 . Then
. Then
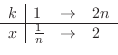 Now let
Now let
 . Then
. Then
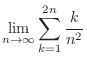 |
 |
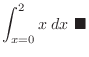 |
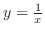 ,
, 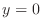 , and the lines
, and the lines 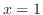 and
and 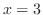
SOLUTION Divide the interval ![$[1,3]$](img2836.png) into
into 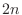 equal subintervals whose length is
equal subintervals whose length is
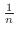 . Then the Riemann sum is
. Then the Riemann sum is
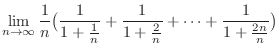 |
 |
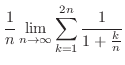 |
|
 |
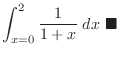 |
Riemann Integrable Functions
Non Integrable Consider a function such that for  a rational number,
a rational number, 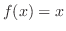 and for
and for  an irrational number,
an irrational number, 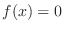 . Then for every interval, there exists a rational number and an irrational number which implies that any Riemann sum can not converge
. Then for every interval, there exists a rational number and an irrational number which implies that any Riemann sum can not converge
From the definition of definite integral, we can obtain the following formula.
Definite Integral Formula
Rules 1. The integral of a sum is the sum of the integrals
2. The integral of a constant multiple is the constant multiple of the integral.
3. Interchange the lower limit and upper limit. Then put minus sign.
4.
5. Inequality is preserved after integration.
Proof
1. Suppose that 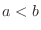 . Then divide the interval
. Then divide the interval ![$[a,b]$](img1050.png) by the partition
by the partition

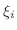 be an element in
be an element in
![$[x_{i-1},x_{i}]$](img2810.png) . Then consider the sum
. Then consider the sum
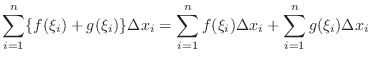
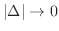 . Then by theorem 3.7,
. Then by theorem 3.7,
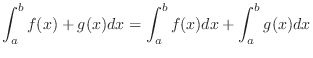
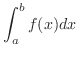 |
 |
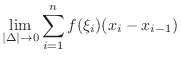 |
|
 |
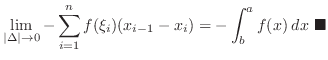 |
Let  be continuous on
be continuous on ![$[a,b]$](img1050.png) . Then consider the function expressed in the integral
. Then consider the function expressed in the integral
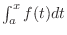 , where
, where  is in
is in ![$[a,b]$](img1050.png) . The domain of this function is
. The domain of this function is ![$[a,b]$](img1050.png) .
.
2nd Fundamental Theorem of Integral Calculus
 is continuous on the closed interval
is continuous on the closed interval ![$[a,b]$](img1050.png) . Then
. Then
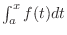 is differentiable with respect to
is differentiable with respect to  and
and
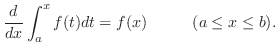
NOTE Suppose that 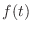 is the speed of a particle. Then
is the speed of a particle. Then
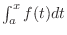 can be thought of the distance traveled by the particle from the time
can be thought of the distance traveled by the particle from the time 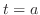 to
to 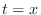 .
.
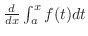 is the derivative at the time
is the derivative at the time  . In other wotds, the speed of a particle. Thus
. In other wotds, the speed of a particle. Thus 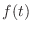 is the speed of a particle at the time
is the speed of a particle at the time 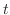 and
and  is the speed of a particle at the time
is the speed of a particle at the time  .
.
| Understanding |
|---|
Let
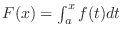 . Then . Then
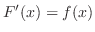 , where , where 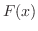 is a primitive function of is a primitive function of  . Thus, a continuous function has a primitive function. . Thus, a continuous function has a primitive function.
|
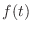 be continuous. Then find
be continuous. Then find
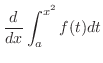
Note that
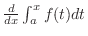 means
means
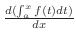 .
SOLUTION
Let
.
SOLUTION
Let 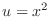 . Then
. Then
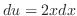 and
and
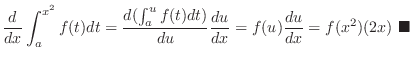
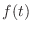 be continuous
be continuous
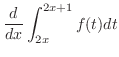
Limits of integration are from 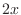 to
to 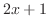 and we can not apply the fundamental theorem of integration. Thus we divide the limits of integration.
SOLUTION Let
and we can not apply the fundamental theorem of integration. Thus we divide the limits of integration.
SOLUTION Let 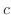 be a constant satisfying
be a constant satisfying
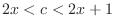 . Then
. Then
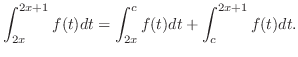
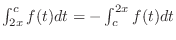
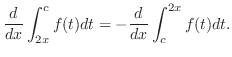
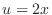 . Then
. Then
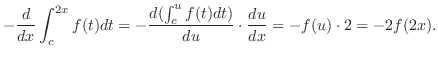
Next let 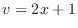 . Then
. Then
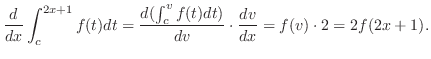

1st Fundamental Theorem of Integral Calculus
 be a continuous function on the close interval
be a continuous function on the close interval ![$[a,b]$](img1050.png) and
and 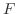 is the indefinite integral of
is the indefinite integral of 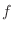 on
on ![$[a,b]$](img1050.png) , then
, then
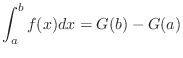
Proof By the 2nd fundamental theorem of integral calculus,
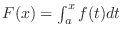 is a primitive function of
is a primitive function of  . Thus,
. Thus,
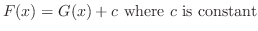 .
Since
.
Since
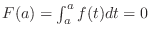 ,
,
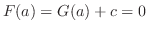 . Thus,
. Thus, 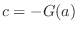 .
From this, we have
.
From this, we have
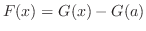 . Set
. Set 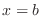 and we have
and we have
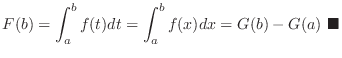
Notation We express
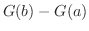 as
as
![$[G(x)]_{a}^{b}$](img2890.png) .
.
Evaluation To evaluate a definite integral, we first find indefinite integral, then subtract the value obtained by substituting the lower limit from the value obtained by substituting the upper limit.
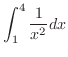 2.
2.
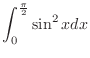 3.
3.
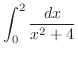
SOLUTION 1.
![$\displaystyle \int_{1}^{4}\frac{1}{x^2}dx = \int_{1}^{4}x^{-2}dx = -\left[\frac...
...} \right]_{1}^{4} = -(\frac{1}{4} - 1) = \frac{3}{4}\ensuremath{ \blacksquare}$](img2894.png)
2.
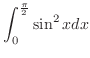 |
 |
![$\displaystyle \int_{0}^{\frac{\pi}{2}}\frac{1-\cos{2x}}{2}dx = \frac{1}{2}\left[x - \frac{\sin{2x}}{2}\right]_{0}^{\frac{\pi}{2}}$](img2896.png) |
|
 |
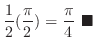 |
To evaluate
![$\left[x - \frac{\sin{2x}}{2}\right]_{0}^{\frac{\pi}{2}}$](img2898.png) , it is better to evaluate
, it is better to evaluate
![$\left[x \right]_0^{\frac{\pi}{2}} - \left[\frac{\sin{2x}}{2}\right]_{0}^{\frac{\pi}{2}}$](img2899.png) . This way, you have less mistakes.
. This way, you have less mistakes.
3.
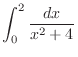 |
 |
![$\displaystyle \frac{1}{2}\left[\tan^{-1}{\frac{x}{2}}\right]_0^2 = \frac{1}{2}\left(\tan^{-1}{\frac{2}{2}} - \tan^{-1}{0}\right)$](img2901.png) |
|
 |
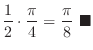 |
Note that if
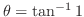 , then
, then
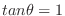 , where
, where
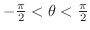 . Thus
. Thus
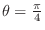 .
.
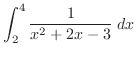 2.
2.
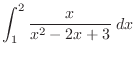
SOLUTION 1. By partial fraction,
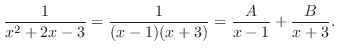
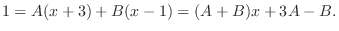
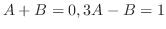 . Thus,
. Thus,
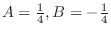 .
.
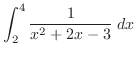 |
 |
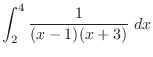 |
|
 |
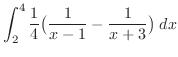 |
||
 |
![$\displaystyle \frac{1}{4}\big[\log\vert x-1\vert -\log\vert{x+3}\vert\big]_2^4$](img2916.png) |
||
 |
![$\displaystyle \frac{1}{4}\big[\log\vert\frac{x-1}{x+3}\vert\big]_2^4$](img2917.png) |
||
 |
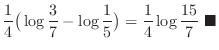 |
| Check |
|---|
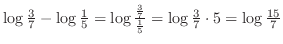 . .
|
| Check |
|---|
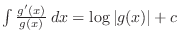
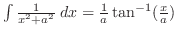 . .
|
| Check |
|---|
Note
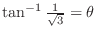 if and only if if and only if
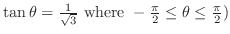 . Thus, . Thus,
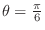 . .
|
2. The determinant 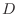 of
of
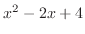 is given by
is given by
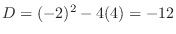 . Thus no more factorization.
. Thus no more factorization.
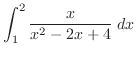 |
 |
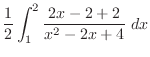 |
|
 |
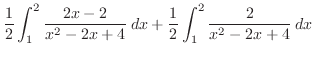 |
||
 |
![$\displaystyle \frac{1}{2}\big[\log\vert x^2 - 2x + 4\vert\big]_1^2 + \int_1^2 \frac{1}{x^2 -2x + 4}\:dx$](img2930.png) |
||
 |
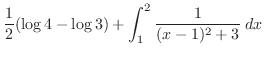 |
||
 |
![$\displaystyle \frac{1}{2}\log\frac{4}{3} + \left[\frac{1}{\sqrt{3}}\tan^{-1}{\frac{x-1}{\sqrt{3}}}\right]_1^2$](img2932.png) |
||
 |
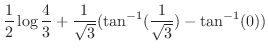 |
||
 |
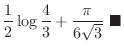 |
|
Exercise A
|
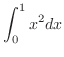
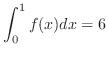 ,
,
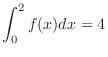 , and
, and
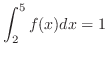 , find the following intgrals
, find the following intgrals
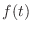 be continuous. Then find
be continuous. Then find 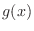
|
Exercise B
|
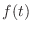 is continous function. Then find
is continous function. Then find