Next: Improper Integral Up: Integration Previous: Definite Integrals Contents Index
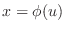 is differentiable on the open interval
is differentiable on the open interval ![$[a,b]$](img1050.png) and
and  is continuous on the closed interval
is continuous on the closed interval
![$[\phi(a), \phi(b)]$](img2969.png) , then
, then
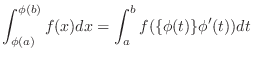
Usage If it is impossible to find the indefinite integral of  , then the following might help.
, then the following might help.
NOTE Let
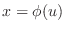 . Then
. Then
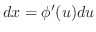 . Now the limit of intervals must be changed from
. Now the limit of intervals must be changed from
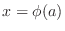 to
to 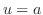 and
and
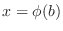 to
to 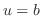 .
.
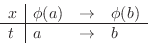 .
.
Integration by Parts
Let
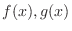 be differentiable on the closed interval
be differentiable on the closed interval ![$[a,b]$](img1050.png) . Then
. Then
![$\displaystyle \int_{a}^{b} f(x)g'(x) = \left[f(x)g(x)\right]_{a}^{b} - \int_{a}^{b} f'(x)g(x)dx $](img2977.png)
Usage We let
 be
be 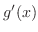 .
.
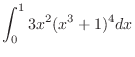 2.
2.
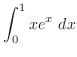
SOLUTION 1. Let
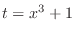 . Then
. Then
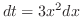 . Thus we can express the integrand as
. Thus we can express the integrand as 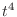 . Furthermore, the limit of integration becomes
. Furthermore, the limit of integration becomes
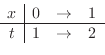 .
.
Thus,
![$\displaystyle{\int_{0}^{1}3x^{2}(x^{3}+1)^{4}dx = \int_{1}^{2}t^4 dt = \left[\f...
... \right ]_{1}^{2} = \frac{32 - 1}{5} = \frac{31}{5}}\ensuremath{ \blacksquare}$](img2984.png)
2.
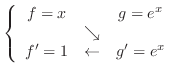 Then
Then
![$\displaystyle \int_{0}^{1}xe^x dx = [xe^x]_{0}^{1} - \int_{0}^{1}e^x dx = e - [e^x]_{0}^{1} = e - (e - 1) = 1.$](img2986.png)
If we let 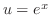 , then
, then
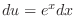 and
and
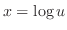 . Thus we can not solve this by u-substitution directly.
. Thus we can not solve this by u-substitution directly.
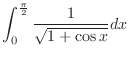
Let
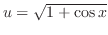 .
.
SOLUTION Let
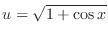 . Then,
. Then,
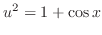 and
and
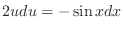 .
.
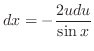 . Now need to express
. Now need to express 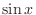 by
by 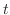 .
.
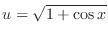 ,
,
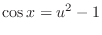 . Thus,
. Thus,
Since
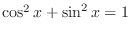 ,
,
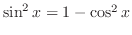 . Thus,
. Thus,
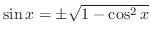 . Note
. Note
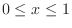 . Thus
. Thus
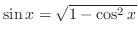 .
.
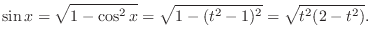
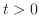 ,
,
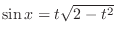 .
.
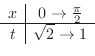 . Thus,
. Thus,
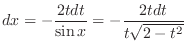
| Check |
|---|
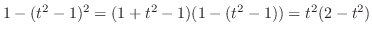 . .
|
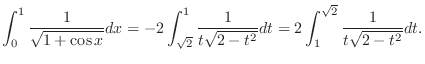
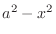 ,
,
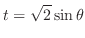 ,
,
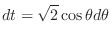 ,
,
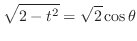 .
.
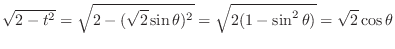
Since the limit of integral is
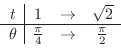 ,
,
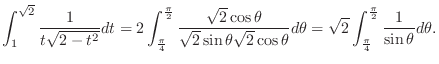
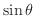 ,
,
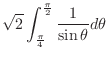 |
 |
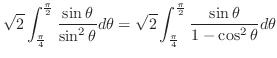 |
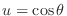 . Then
. Then
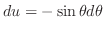 ,
,
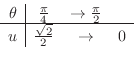 . Thus,
. Thus,
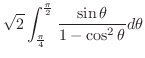 |
 |
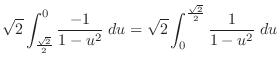 |
|
 |
![$\displaystyle \frac{\sqrt{2}}{2}\left[\log\vert\frac{1+u}{1-u}\vert\right]_{0}^...
...1 + \frac{\sqrt{2}}{2}}{1 - \frac{\sqrt{2}}{2}}\vert\ensuremath{ \blacksquare}$](img3022.png) |
| u-substitution |
|---|
In u-substitution, complexity of integration depends on the choice of  .
Alternative Solution .
Alternative Solution
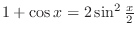
|
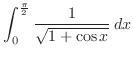 |
 |
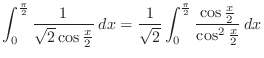 |
|
 |
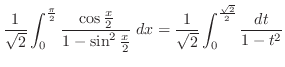 |
||
 |
![$\displaystyle \frac{\sqrt{2}}{2}\left[\log\vert\frac{1+t}{1-t}\vert\right]_0^{\...
...1 + \frac{\sqrt{2}}{2}}{1 - \frac{\sqrt{2}}{2}}\vert\ensuremath{ \blacksquare}$](img3027.png) |
Properties of Definite Integral Suppose that  is continuous on the limit of integration.
is continuous on the limit of integration.
1. If  is even function, then
is even function, then
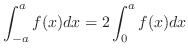
2. If  is odd function, then
is odd function, then
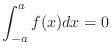
3.
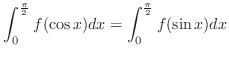
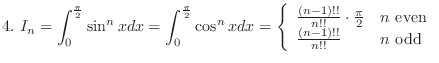
where
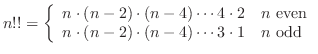
Even/Odd Functions  is even function means that
is even function means that
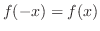 and the graph of a function
and the graph of a function  is symmetric with respect to the
is symmetric with respect to the  -axis. Thus,
-axis. Thus,
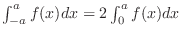 .
.
 is odd function means that
is odd function means that
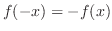 and the graph of a function
and the graph of a function  is symmetric with respect to the
is symmetric with respect to the  -axis. Thus,
-axis. Thus,
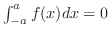 .
.
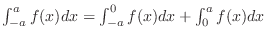 . Now
. Now  is even function and
is even function and
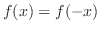 . Thus,
. Thus,
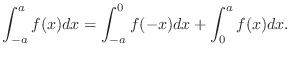
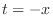 . Then
. Then 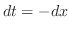 .
.
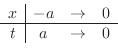 .
.
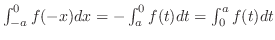 . Thus,
. Thus,
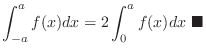
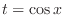 . Then
. Then
Since
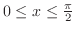 , we have
, we have
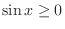 and
and
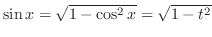 .
.
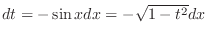 ,
,
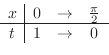 ,
,
| Check |
|---|
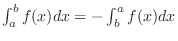 . .
|
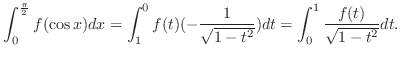
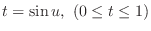 and
and
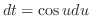 . Also,
. Also,
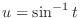 ,
,
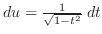 ,
,
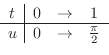 . Thus,
. Thus,
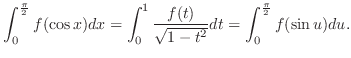
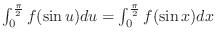
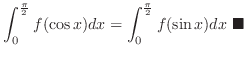
4. By 3.
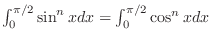 . We show
. We show
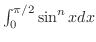 .
.
For 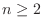 ,
,
| Check |
|---|
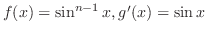 , ,
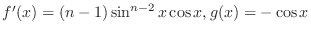 . .
|
 |
 |
![$\displaystyle \int_{0}^{\frac{\pi}{2}}\sin^{n-1}{x}\sin{x}dx = -\left[\sin^{n-1}{x}\cos{x}\right]_{0}^{\frac{\pi}{2}}$](img3063.png) |
|
 |
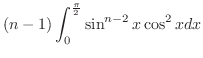 |
 . Thus
. Thus
![$\left[\sin^{n-1}{x}\cos{x}\right]_{0}^{\frac{\pi}{2}} = 0$](img3066.png) . Now we take care of the rest.
. Now we take care of the rest.
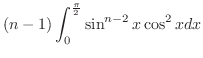 |
 |
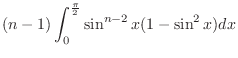 |
|
 |
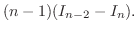 |
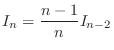 . Note
. Note
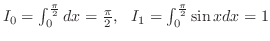 ,
,
| Check |
|---|
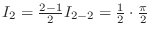
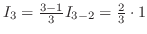
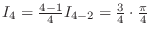
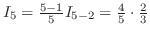 . .
|
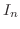 |
 |
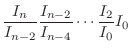 |
|
 |
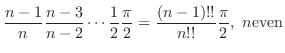 |
||
 |
 |
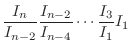 |
|
 |
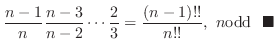 |
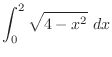
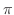 .
The inside of square root is of the form
.
The inside of square root is of the form 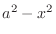 . Let
. Let
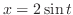 and
and
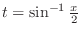 ,
,
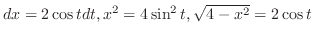 ,
,
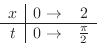 . Thus
. Thus
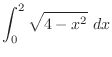 |
 |
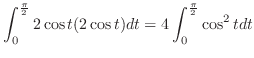 |
|
 |
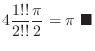 |
|
Exercise A
|
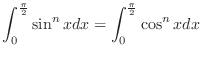
 be a continuous function on the interval
be a continuous function on the interval
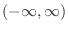 . Then answer the following question concerning the function
. Then answer the following question concerning the function
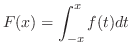
(a) Show that 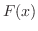 is an odd function
is an odd function
(b) Show that  is even function implies that
is even function implies that 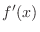 is an odd function.
is an odd function.
(c) Show that
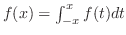 implies that
implies that 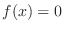
(d) Show that  can be represented by a sum and a difference of functions
can be represented by a sum and a difference of functions