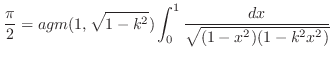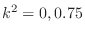Next: Application of Definite Integrals Up: Integration Previous: Evaluating Definite Integral Contents Index
The definite integral we have studied so far can only apply to the continuous functions. Now we extend this definition to the function with finite number of discontinuity.
1st kind Improper Integral of the 1st kind applies to the case where the function has discontinuous points in the limit of integral.
If the integrand is continuous on ![$(a,b]$](img3101.png) and discontinuous at
and discontinuous at  , then integrate from
, then integrate from
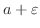 to
to 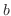 . Then find the limit as
. Then find the limit as
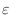 approaches 0 from the right.
approaches 0 from the right.
Note that the integral from
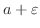 to
to 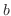 is the definite integral.
is the definite integral.
Improper Integral of the 1st kind
[1] If  is continuous on
is continuous on ![$(a,b]$](img3101.png) and discontinuous at
and discontinuous at  . Then
. Then  is continuous on the interval
is continuous on the interval
![$[a + \varepsilon, b]$](img3104.png) . Thus we can think of the following definite integral
. Thus we can think of the following definite integral
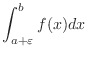
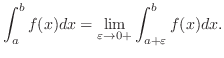
 is continuous on
is continuous on 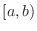 and discontinuous at
and discontinuous at 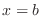 . Then
. Then  is continuous on the interval
is continuous on the interval
![$[a, b - \varepsilon]$](img3108.png) . Thus we can think of the following definite integral
. Thus we can think of the following definite integral
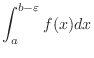
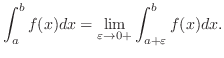
1.
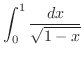 2.
2.
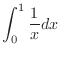
First use u-substitution to make the integrand simple function. Then solve improper integral.
SOLUTION
1. Let
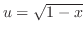 . Then
. Then 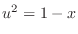 and
and
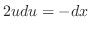 .
.
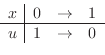 ,
,
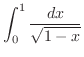 |
 |
![$\displaystyle \int_1^0\frac{-2udu}{u} = \int_0^1 \frac{2}{u}du = \lim_{\varepsi...
...\varepsilon \to 0+}\left[2t\right]_\varepsilon^1 = 2\ensuremath{ \blacksquare}$](img3117.png) |
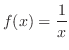 is continuous on
is continuous on ![$(0,1]$](img3119.png) and antiderivative of
and antiderivative of  is
is 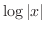 .
.
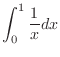 |
 |
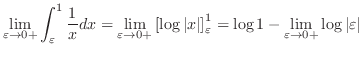 |
|
 |
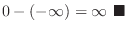 |
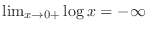 .
.
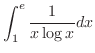 2.
2.
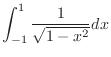
SOLUTION 1.
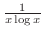 is continuous on
is continuous on ![$(0,e]$](img3129.png) , but discontinuous at
, but discontinuous at 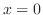 . Let
. Let
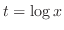 . Then
. Then
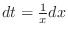 ,
,
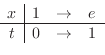 ,
,
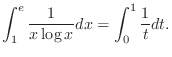
 is not continuous at
is not continuous at  .
.
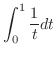 |
 |
![$\displaystyle \lim_{\varepsilon \to 0+}\int_\varepsilon^1 \frac{1}{t}dt = \lim_...
...}\right]_{\varepsilon}^1 = \log{1} - \lim_{\varepsilon \to 0+}\log{\varepsilon}$](img3137.png) |
|
 |
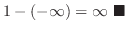 |
Since the function is not continuous at 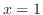 , we may write
, we may write
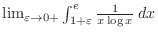 . But it is better to take u-substitution first.
. But it is better to take u-substitution first.
2.
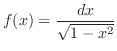 is continuous on
is continuous on
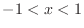 , but not continuous at
, but not continuous at 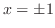 . Then we write
. Then we write
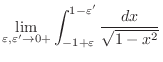
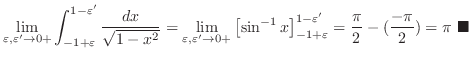
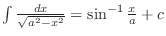 .
.
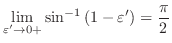 .
.
Improper Integral of the 1st kind
[3]  is discontinuous at
is discontinuous at
![$c_{1},c_{2},\ldots,c_{n} \in [a,b
]$](img3148.png) . Then divide the interval
. Then divide the interval ![$[a,b]$](img1050.png) into subintervals
into subintervals
![$[a,c_{1}],[c_{1},c_{2}],\ldots,[c_{n},b]$](img3149.png) . Now consider the improper imtegral on each subintervals. If all improper integrals exist, then we define the sum of improper integrals as improper integral of
. Now consider the improper imtegral on each subintervals. If all improper integrals exist, then we define the sum of improper integrals as improper integral of  on
on ![$[a,b]$](img1050.png) .
.
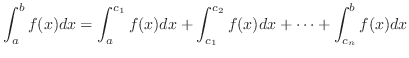
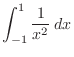
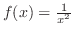 is not continuous at
is not continuous at 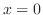 . Then we write
. Then we write
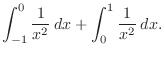
![$\displaystyle \int_{0}^{1}\frac{1}{x^2}\:dx = \lim_{\varepsilon \to 0+}\int_{\v...
...on \to 0+}\left[-\frac{1}{x}\right]_{\varepsilon}^{1} = -(1 - \infty) = \infty.$](img3154.png)

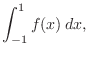

SOLUTION  is not continuous at
is not continuous at 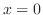 . Then we write the integral as follows:
. Then we write the integral as follows:
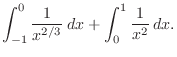
![$\displaystyle \int_{-1}^{0}\frac{1}{x^{2/3}}\:dx = \lim_{\varepsilon \to 0-}\in...
...im_{\varepsilon \to 0-}\left[3x^{1/3}\right]_{-1}^{\varepsilon} = 0 - (-3) = 3.$](img3160.png)
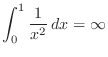 . Thus we can conclude that no improper integral exists
. Thus we can conclude that no improper integral exists
 2nd kind Improper integral of the 2nd kind is infinite integral.
2nd kind Improper integral of the 2nd kind is infinite integral.
Improper Integral of the 2nd kind
 is continuous on
is continuous on
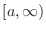 . Then
. Then  is continuous on
is continuous on ![$[a,b]$](img1050.png) , where
, where
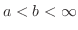 . Then we define the infinite integral using the limit of
. Then we define the infinite integral using the limit of
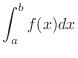 .
.
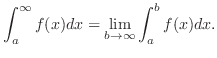
 is continuous on
is continuous on
![$(-\infty,b]$](img3167.png) .
.
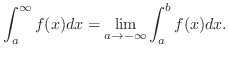
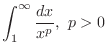
This improper integral is used to find the convergence and divergence of other integral. For example,
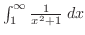 is less than
is less than
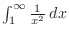 and
and
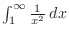 converges. Thsu, converges.
SOLUTION
For
converges. Thsu, converges.
SOLUTION
For 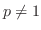 ,
,
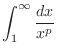 |
 |
![$\displaystyle \lim_{b \to \infty}\int_{1}^{b}\frac{1}{x^{p}}\:dx = \lim_{b \to ...
...}\int_1^b x^{-p}\:dx = \lim_{b \to \infty}\frac{1}{1-p}\left[x^{1-p}\right]_1^b$](img3174.png) |
|
 |
![$\displaystyle \lim_{b \to \infty} \frac{1}{1-p}(b^{1-p} - 1) = \left\{\begin{array}{cl}
\frac{1}{p-1}, & p > 1\\
\infty, & p < 1
\end{array}\right].$](img3175.png) |
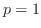 ,
,
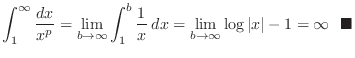
If  is continuous on
is continuous on
 and
and
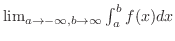 exists, then we express this limit
exists, then we express this limit
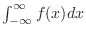 .
.
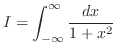
SOLUTION
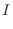 |
 |
![$\displaystyle \lim_{{a \rightarrow -\infty}, {b \rightarrow \infty}}\int_{a}^{b...
...{1+x^{2}} = \lim_{a \to -\infty, b \to \infty}\left[\tan^{-1}{x}\right]_{a}^{b}$](img3182.png) |
|
 |
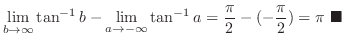 |
Gamma Function
Let
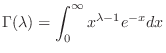 . Then
. Then
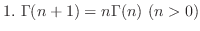
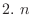 is natural number
is natural number
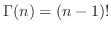
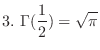
Gamma Function Gamma function was created to extend the factorial.
Proof
1.
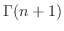 |
 |
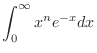 |
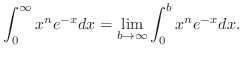
Using integration by parts,
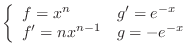
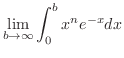 |
 |
![$\displaystyle \lim_{b \to \infty}\left[x^{n}(-e^{-x}) \right ]_{0}^{b} - \lim_{b \to \infty}\int_{0}^{b}nx^{n-1}(-e^{-x}) dx$](img3194.png) |
|
 |
![$\displaystyle \lim_{b \to \infty}\left[-x^{n}(e^{-x}) \right ]_{0}^{b} + n\lim_{b \to \infty}\int_{0}^{b}x^{n-1}(e^{-x}) dx$](img3195.png) |
||
 |
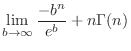 |
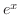 |
|---|
Maclaurin series expansion of 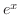 is one of the most important series expansion. As we know the derivative of is one of the most important series expansion. As we know the derivative of 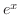 is is 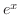 . Then in the Maclaurin series expansion, every term is the derivative of the next term. Thus, . Then in the Maclaurin series expansion, every term is the derivative of the next term. Thus,
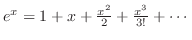 . .
|
To find
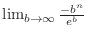 , we use the Maclaurin series expansion of
, we use the Maclaurin series expansion of 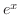 .
.
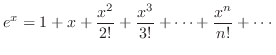
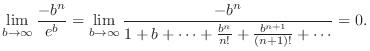
2. By 1. for 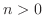 , we have the recurrence relation
, we have the recurrence relation
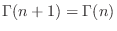 .
.
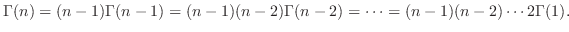
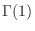 |
 |
![$\displaystyle \int_{0}^{\infty}e^{-x} dx = \lim_{b \to \infty}\int_0^b e^{-x}dx...
...lim_{b \to \infty}\left[-e^{-x}\right]_0^b = -\lim_{b \to \infty}e^{-b} + 1 = 1$](img3205.png) |
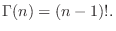
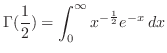 . Then let
. Then let
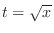 . Then
. Then 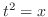 ,
,
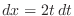 .
.
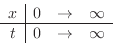 . Thus,
. Thus,
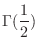 |
 |
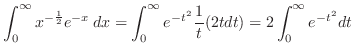 |
 |
|---|
It is impossible to find
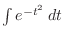 . In other words, we can not express the indefinite integral of . In other words, we can not express the indefinite integral of 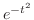 using elementary functions. using elementary functions.
|
In Example5.5, we have shown
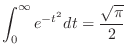 . Thus
. Thus
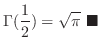
|
Exercise A
|
|
Exercise B
|
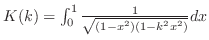 is called the complete elliptic integral of the 1st kindLet
is called the complete elliptic integral of the 1st kindLet
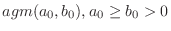 be the arithmetic mean. Then the following is known
be the arithmetic mean. Then the following is known