Next: Definite Integrals Up: Integration Previous: Integration of Trigonometric Functions Contents Index
Rational Function 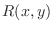 If
If 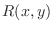 is expressed by the fraction of polynomials, then we say
is expressed by the fraction of polynomials, then we say 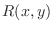 is a rational function of
is a rational function of  and
and  .
.
Sum of Squares Let 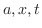 be such that hypoteneus represents a sum of squares.
be such that hypoteneus represents a sum of squares.
DIfference of Squares Let 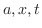 be such that adjacent represents the difference of squares.
be such that adjacent represents the difference of squares.
Integration of Irrational Functions Suppose that 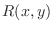 is a rational function of
is a rational function of  and
and  . Then
. Then
1.
![$\displaystyle{\int R(x,\sqrt[n]{\rm linear polynomial })dx}$](img2733.png)
Let
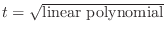 . Then we can get integration of rational function.
. Then we can get integration of rational function.
[2]

1. 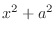 after completing the square. Then let
after completing the square. Then let
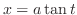
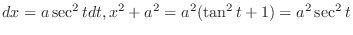
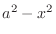 after completing the square. Then let
after completing the square. Then let
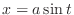
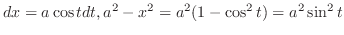
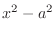 after completing the square, Then let
after completing the square, Then let
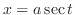
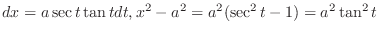
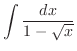 2.
2.
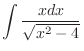
By substitution, integration of irrational function should be expressed by integration of rational function.
SOLUTION
1. Let
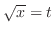 . Then
. Then 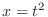 and
and
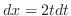 . Thus
. Thus
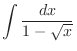 |
 |
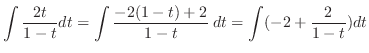 |
|
 |
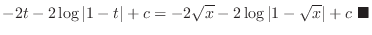 |
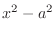 . Let
. Let
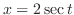 . Then
. Then
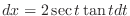 . Note that
. Note that
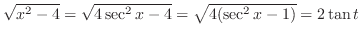 . Thus
. Thus
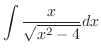 |
 |
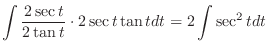 |
|
 |
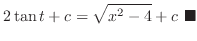 |
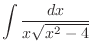 2.
2.
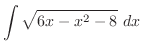
This problem should be solved by taking
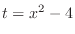 ,
,
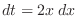 . But to show how nice to use a trigonometric substitution, we solve this by trinometric substitution.
. But to show how nice to use a trigonometric substitution, we solve this by trinometric substitution.
SOLUTION
1. Let
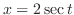 . Then
. Then
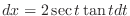 ,
,
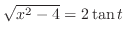 . Thus,
. Thus,
Note that when
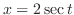 , then we do not express
, then we do not express
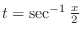 . Instead,
. Instead,
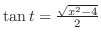 and
and
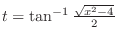 .
.
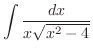 |
 |
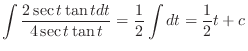 |
|
 |
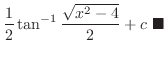 |
| Exercise3-12-2. |
|---|
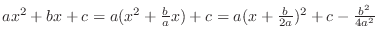 . .
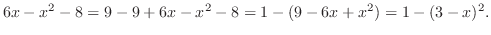
|
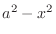 . Thus conside the right triangle with the hypotenuse
. Thus conside the right triangle with the hypotenuse 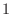 , the opposite side of the angle
, the opposite side of the angle 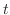 is
is 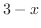 .
.
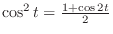
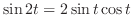 .
.
Let
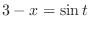 .
.
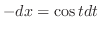 .
.
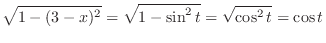
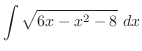 |
 |
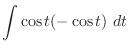 |
|
 |
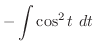 |
||
 |
![$\displaystyle -\int{\frac{1 + \cos{2t}}{2}} dt = -[\frac{t}{2} + \frac{\sin{2t}}{4}] + c$](img2778.png) |
||
 |
![$\displaystyle -[\frac{t}{2} + \frac{\sin{t}\cos{t}}{2}] + c$](img2779.png) |
||
 |
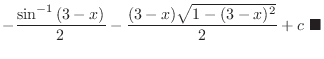 |
|
Exercise A
|
|
Exercise B
|