Next: Integration of Irrational Functions Up: Integration Previous: Integration of Rational Functions Contents Index
Integration of Trigonometric Functions[I]
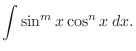
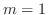 . Let
. Let
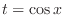 . Then
. Then
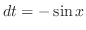 and
and
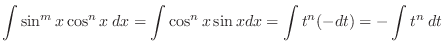
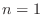 . Let
. Let
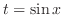 . Then
. Then
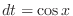 and
and
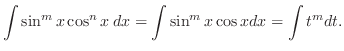
Understanding By substitution, the integration of a trinometric function can be solved by integration of a rational function.
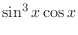
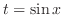 . Thne
. Thne
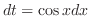 ,
,
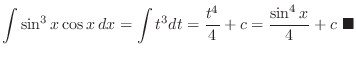
Which function
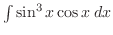 is the same as
is the same as
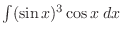 . Now which function should be put
. Now which function should be put 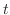 .
.
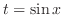 or
or
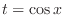 are possibilities. But letting
are possibilities. But letting
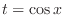 , we have
, we have
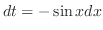 and it is impossible to express integrand and
and it is impossible to express integrand and 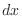 interms of a function of
interms of a function of 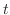 and
and 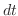 .
.
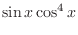
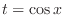 . Then
. Then
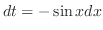 .
.
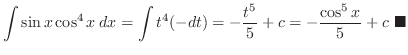
Integration of Trigonometric Functions[I]
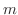 is odd, then
is odd, then 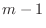 is even. Using
is even. Using
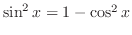 , express
, express
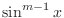 as in the form of
as in the form of 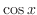 . Thus,
. Thus,
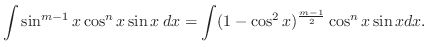
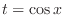 . Then
. Then
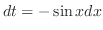 and
and
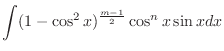 |
 |
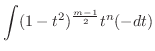 |
 odd.
odd.
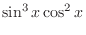
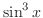 is odd power of
is odd power of 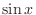 ,
,
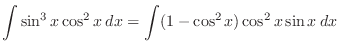
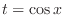 . Then
. Then
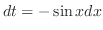 and
and
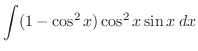 |
 |
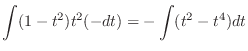 |
|
 |
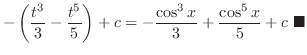 |
If there is an odd power, then use
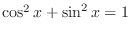 to write
to write
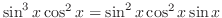 .
.
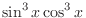 .
.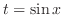 . Then
. Then
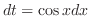 and
and
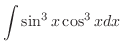 |
 |
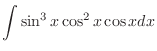 |
|
 |
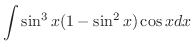 |
||
 |
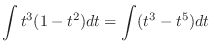 |
||
 |
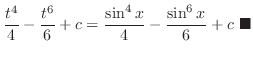 |
Since the power of 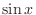 and the power of
and the power of 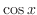 are odd, we can use either one of them.
are odd, we can use either one of them.
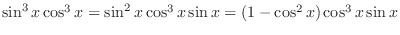 .
.
Trig 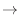 Rational Function Rational Function |
|---|
Let
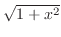 be the hypoteneus of the right triangle. Then be the hypoteneus of the right triangle. Then
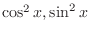 can be expressed as rational functions. Also note that the derivative of can be expressed as rational functions. Also note that the derivative of 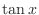 is expressed as a square of a function is expressed as a square of a function
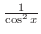 . .
|
Integration of Trigonometric Function[I]
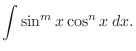
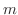 and
and  are both even. Now let
are both even. Now let
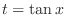 . Then we can express
. Then we can express
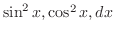 by using
by using 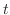 . Consider the right triangle with the adjacent of the angle
. Consider the right triangle with the adjacent of the angle  is 1 and the opposite is
is 1 and the opposite is 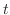 . Then
. Then
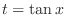 and
and
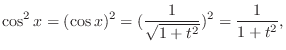
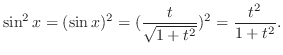
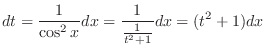
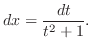
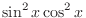 2.
2.
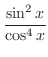
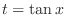 , it is easier to use double angle formula.
, it is easier to use double angle formula.
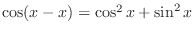 ,
,
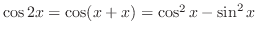 . Thus adding both sides of equation,
. Thus adding both sides of equation,
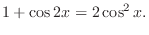
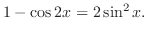
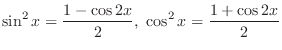
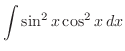 |
 |
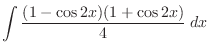 |
|
 |
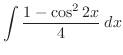 |
||
 |
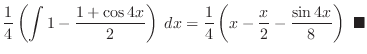 |
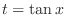 . Then
. Then
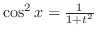 ,
,
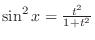 ,
,
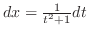 . Thus
. Thus
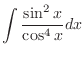 |
 |
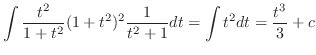 |
|
 |
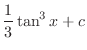 |
| Check |
|---|
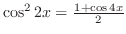 . .
|
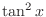 2.
2.
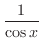
1. Let
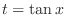 and express
and express
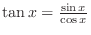 . Then
. Then
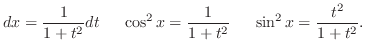
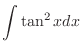 |
 |
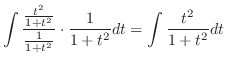 |
|
 |
![$\displaystyle \int \frac{1 + t^{2} - 1}{1+ t^{2}} dt = \int [1 - \frac{1}{1+ t^2}] dt$](img2658.png) |
||
 |
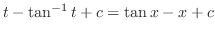 |
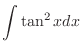 |
 |
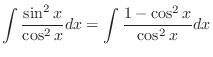 |
|
 |
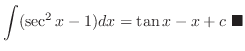 |
2.
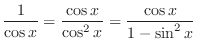 . Then it is in the form of [1]-2.
. Then it is in the form of [1]-2.
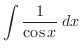 |
 |
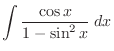 |
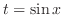 and
and
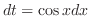
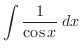 |
 |
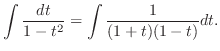 |
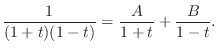
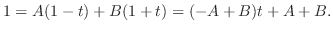
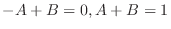 . Then
. Then
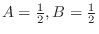 .
Thus,
.
Thus,
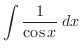 |
 |
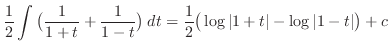 |
|
 |
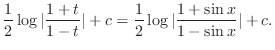 |
Alternative Solution
 . Thus,
. Thus,
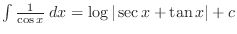
Note that
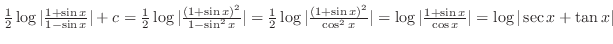 .
.
 The substitution by
The substitution by
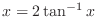 is applied at the last choice.
is applied at the last choice.
The hypoteneus is given by
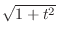 and the angle is given by
and the angle is given by
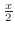 . Then every trigonometric function can be expressed as a rational function.
. Then every trigonometric function can be expressed as a rational function.
Integration of Trigonometric Functions[II]
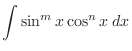
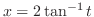 . Then
. Then
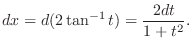
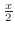 ,the adjacent to the angle 1, and opposite to the angle
,the adjacent to the angle 1, and opposite to the angle 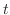 .
.
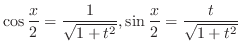
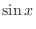 |
 |
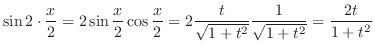 |
|
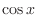 |
 |
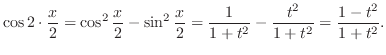 |
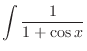 .
. 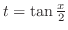 ,
,
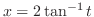 .
.
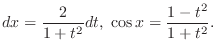
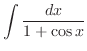 |
 |
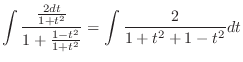 |
|
 |
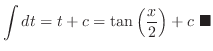 |
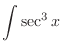 .
.
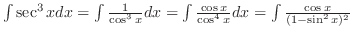 .
.
| Check |
|---|
Exercise3-10-2. By alternative solution,
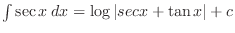 . .
|
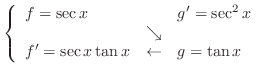
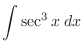 |
 |
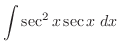 |
|
 |
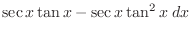 |
||
 |
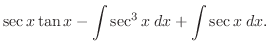 |
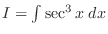 . Then
. Then
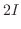 |
 |
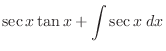 |
|
 |
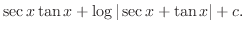 |
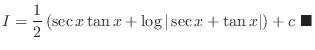
|
Exercise A
|
|
Exercise B
|