Next: Integration of Trigonometric Functions Up: Integration Previous: Integration by Parts Contents Index
If  and
and 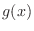 are polynomials, then the integral of quotient of
are polynomials, then the integral of quotient of  and
and 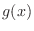 , which is
, which is
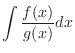 , can be obtained by the following method.
, can be obtained by the following method.
Partial Fractions
If
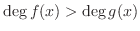 , then let
, then let 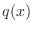 be the quotient of
be the quotient of  and
and 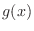 and the remainder be
and the remainder be 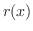 . Thus
. Thus

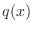 is a polynomial. It is easy to integrate.
is a polynomial. It is easy to integrate.
Check
1. If the degree of a numerator is larger than the degree of a denominator, then divide.
2. Factor the denominator. The number of multiplicity becomes the number of partial fractions.
3. Prodeed partial fraction expansion.
Factoring Denominator Fundamental Theorem of Algebra states that every polynomial can be factored into the product of linear and quadratic polynomials.
Partial Fraction Decomposition A partial fraction decomposition is the operation that consists in expressing the fraction as a sum of a polynomial and one or several fractions whose degree of numerator is one less than the degree of denominator.
NOTE The foctors of the denominator is
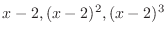 . Thus we need 3 partial fractions. Now inside of parenthesis, we have linear polynomial. Thus, the numerators must be constant.
. Thus we need 3 partial fractions. Now inside of parenthesis, we have linear polynomial. Thus, the numerators must be constant.
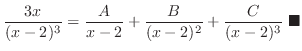
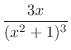
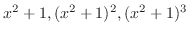 . Thus we need three partial fractions. Now inside of parenthesis, we have quadratic polynomial. Thus, the numerators must be linear.
. Thus we need three partial fractions. Now inside of parenthesis, we have quadratic polynomial. Thus, the numerators must be linear.
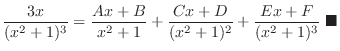
Solving Partial Fraction by System of Linear Equations
Clear the denominator. Then we a polynomials in both sides of equation. Since the equation must be satisfied by all  , the coefficients of two polynomials of the same degree are equal. From this, we get a system of linear equations. Finally solve the system to get
, the coefficients of two polynomials of the same degree are equal. From this, we get a system of linear equations. Finally solve the system to get
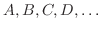 .
.
| Shortcoming |
|---|
| The method we introduced has some shortcoming. When the degree of denominato gets large. the number of equation in the system gets large, and almost impossible to calculate. Then we introduce other technique called Heaviside Mrthodto solve a patial fraction. |
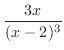
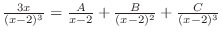 . Clear the denominator and let
. Clear the denominator and let 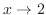 . Then
. Then
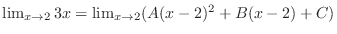 . Then
. Then 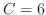 . This is a part of Heaviside method..
SOLUTION
By Example3.5,
. This is a part of Heaviside method..
SOLUTION
By Example3.5,
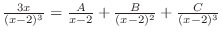 . Now clear the denominator and simplify to get
. Now clear the denominator and simplify to get
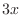 |
 |
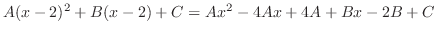 |
|
 |
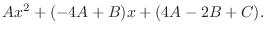 |
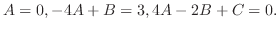
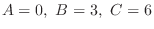 ,
,
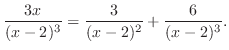
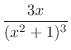
The degree of the polynomial inside a parenthesis is two and the degree of the numerator is one. Then no more partial fraction decomposition.
SOLUTION
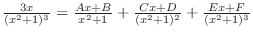 . Clear the denominator,
. Clear the denominator,
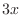 |
 |
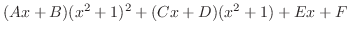 |
|
 |
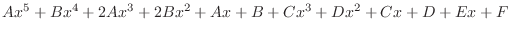 |
||
 |
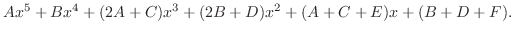 |
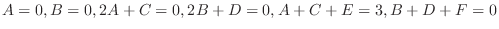 .
Then
.
Then
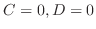 , Since
, Since
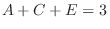 ,
, 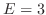 ,
, 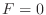 . Therefore,
. Therefore,
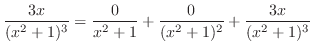
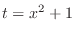 , then we can solve this problem.
, then we can solve this problem.

Partial Fraction of Rational Function Every rational function
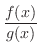 can be decomposed by partial fraction to get a sum of the following functions..
can be decomposed by partial fraction to get a sum of the following functions..
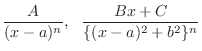
Let
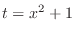 . Then
. Then
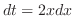 and
and
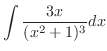 |
|||
 |
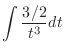 |
||
 |
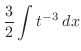 |
||
 |
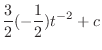 |
||
 |
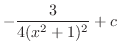 |
If we let 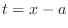 . Then it is given in one of the following forms.
. Then it is given in one of the following forms.
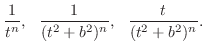
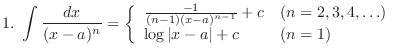
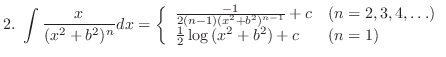
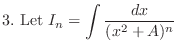 . Then the following recurrence relation holds.
. Then the following recurrence relation holds.
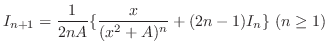
Proof
1. Let 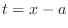 . Then
. Then 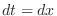 and
and
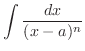 |
 |
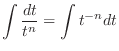 |
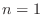 , we have
, we have
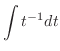 |
 |
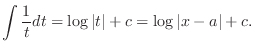 |
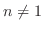 ,
,
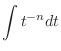 |
 |
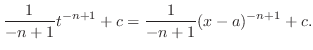 |
2. Let
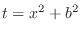 . Then
. Then 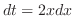 and
and
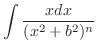 |
 |
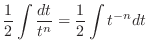 |
For 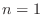 , we have
, we have
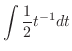 |
 |
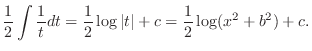 |
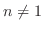 ,
,
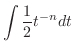 |
 |
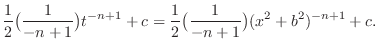 |
| Check |
|---|
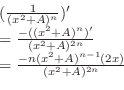 . .
|
3. Integration by parts, we have
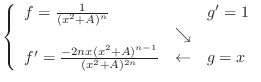 . Then
. Then
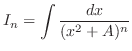 |
 |
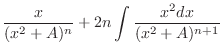 |
|
 |
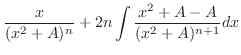 |
||
 |
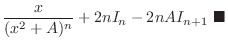 |
| Check |
|---|
Express
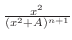 as as
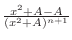
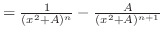 . .
|
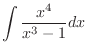
Instead of dividing 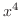 by
by 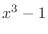 , write
, write
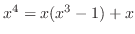 to get the same result.
SOLUTION
to get the same result.
SOLUTION
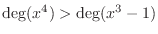 . Thus divide the numerator by the denominator.
. Thus divide the numerator by the denominator.
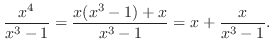
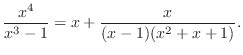
| Check |
|---|
Since the denominator is 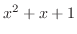 , the numerator must be a linear polynomial. , the numerator must be a linear polynomial.
|
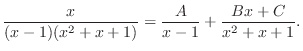 |
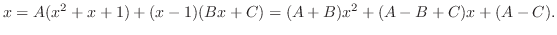
Setting the coefficient of the same degree is equal.
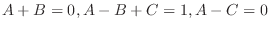
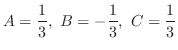 .
Thus
.
Thus
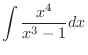 |
 |
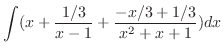 |
|
 |
![$\displaystyle \frac{1}{2}x^{2} + \frac{1}{3}\log{\vert x-1\vert} - \frac{1}{3}[\int \frac{x-1}{x^2 + x+ 1} dx]$](img2546.png) |
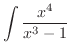 |
 |
![$\displaystyle \frac{1}{2}x^{2} + \frac{1}{3}\log{\vert x-1\vert} - \frac{1}{3}[\int \frac{x-1}{(x +\frac{1}{2})^{2} + \frac{3}{4}} dx]$](img2548.png) |
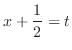 . Then
. Then
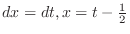 .
.
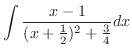 |
 |
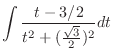 |
|
 |
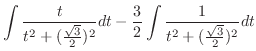 |
||
 |
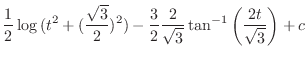 |
||
 |
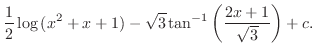 |
| Check |
|---|
The degree of the denominator of
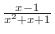 is two. Complete the square. is two. Complete the square.
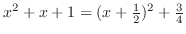 . .
|
| Check |
|---|
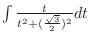 . Let . Let
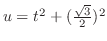 and and
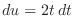 . .
 . .
|
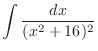
SOLUTION Let
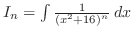 . Then
. Then
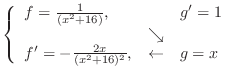
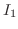 |
 |
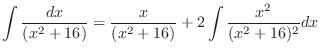 |
|
 |
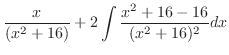 |
||
 |
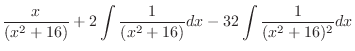 |
||
 |
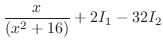 |
| Check |
|---|
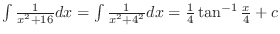 . .
|
![$\displaystyle I_{2} = \frac{1}{32}[\frac{x}{(x^2 + 16)} + I_{1}] = \frac{1}{128}[\frac{4x}{(x^2 + 16)} + \tan^{-1}(\frac{x}{4})] + c$](img2571.png)
|
Exercise A
|
|
Exercise B
|