Next: Integration Up: Extreme Value of Functions Previous: Curve Sketching Contents Index
Polar Coordinates
Let P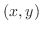 be a point on a plane. Then we represent P as a polar coordinate. Let the origin O be a pole. Then consider ray from the origin. In this case,
be a point on a plane. Then we represent P as a polar coordinate. Let the origin O be a pole. Then consider ray from the origin. In this case,  -axis is called a polar axis and the angle
-axis is called a polar axis and the angle 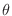 formed by ray and polar axis is called argument. Let
formed by ray and polar axis is called argument. Let 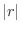 be the distance between the origin and a point P. Then the position of P can be expressed as a pair such as
be the distance between the origin and a point P. Then the position of P can be expressed as a pair such as
![$[r, \theta]$](img2149.png) . Now we call this pair
. Now we call this pair
![$[r, \theta]$](img2149.png) polar coordinate of P.
polar coordinate of P.
![$[r, \theta]$](img2149.png) Note that
Note that 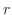 can be negative.
can be negative.
NOTE Let a rectangular coordinate of P be 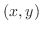 and a polar coordinate of P be
and a polar coordinate of P be
![$[r, \theta]$](img2149.png) . Then we have
. Then we have
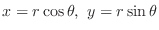
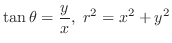
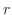 and
and 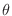 , P
, P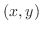 is fixed. On the other hand, even P
is fixed. On the other hand, even P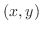 is given, the value of
is given, the value of 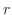 and
and 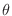 can not be determined uniquely.
can not be determined uniquely.
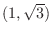 .
.
SOLUTION
Since
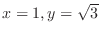 ,
,
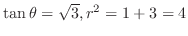 . Thus the point P is on the ray
. Thus the point P is on the ray
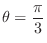 and the distance from the origin is 2. Thus the rectangular coordinate of P can be expressed as
and the distance from the origin is 2. Thus the rectangular coordinate of P can be expressed as
![$\displaystyle{[2,\frac{\pi}{3}]}$](img2157.png) . Note that
. Note that
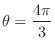 and
and 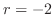 also represents the point P.
also represents the point P.

![$[1,\frac{\pi}{3}]$](img2160.png) .
. 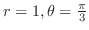
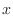 |
 |
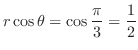 |
|
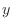 |
 |
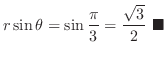 |
Polar Equation
Suppose the curve of a function is given by rectangular coordinates
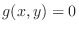 . Then the equation expressed by the polar coordinates ,
. Then the equation expressed by the polar coordinates ,
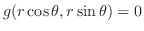
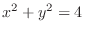
Setting
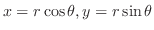 and eliminate
and eliminate 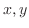 .
.
SOLUTION
Let
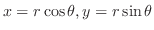 . Then we have
. Then we have
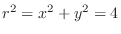 which implies
which implies 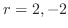

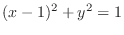
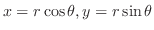 . Then
. Then
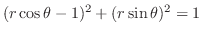
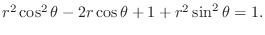 Simplifying,
Simplifying,
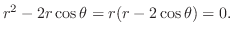 From this,
From this,
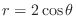

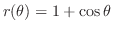
If
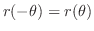 , then for positive
, then for positive 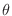 and negative
and negative 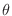 give the same
give the same 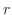 . Thus, the curve is symmetric with respect to the
. Thus, the curve is symmetric with respect to the  -axis.
-axis.
SOLUTION 1. Since
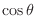 is a even function, we have
is a even function, we have
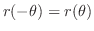 . Thus it is symmetric with respect to the
. Thus it is symmetric with respect to the  -axis. Thus to draw the curve of a function, we only need to check from
-axis. Thus to draw the curve of a function, we only need to check from
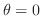 to
to
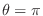 .
.
2. Next we write a table for a polar coordinates of a curve.
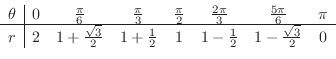

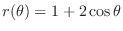
SOLUTION
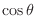 is even implies
is even implies
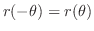 . Thus it's curve is symmetric with respect ot the
. Thus it's curve is symmetric with respect ot the  -axis.
-axis.
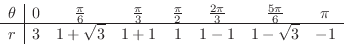

|
Exercise A
|
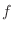 and the local extreme values. Describe the concavity of the graph of
and the local extreme values. Describe the concavity of the graph of 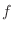 and find the points of inflection.
and find the points of inflection.
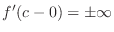 and
and
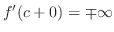 , we say
, we say 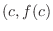 is a vertical cusp
is a vertical cusp
|
Exercise B
|
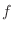 and describe the concavity of the graph of
and describe the concavity of the graph of 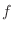
(a)
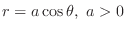 (circle)
(circle)
(b)
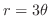 , Archmedes' spiral
, Archmedes' spiral
(c)
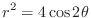 Bernoulli's lemniscate
Bernoulli's lemniscate