Next: . Up: ANSWERS Previous: . Contents Index
1.
2.
(a) Concave up on
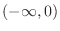 , concave down on
, concave down on
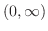 , local minimum
, local minimum 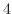 at
at 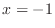 , local minimum 0 at
, local minimum 0 at 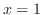 , inflection point
, inflection point 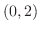
(b) Concave up on
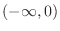 , concave down on
, concave down on
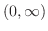 , locla maximum
, locla maximum 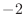 at
at 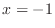 , local minimum
, local minimum 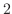 at
at 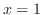
(c) Concave up on
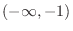 , concave down on
, concave down on
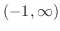 , local maximum
, local maximum
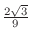 at
at
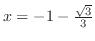 local minimum
local minimum
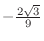 at
at
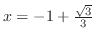 , inflection point
, inflection point 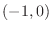
(d) Concave up on
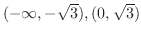 , concave down on
, concave down on
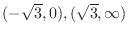 , local minimum
, local minimum
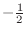 at
at 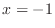 , local maximum
, local maximum
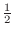 at
at 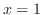 ,
,
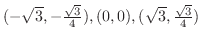 are points of inflection.
are points of inflection.
(e) concave up on 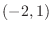 , concave down on
, concave down on
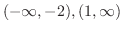 , local minimum 0 at
, local minimum 0 at 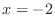 and
and 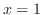 , local maximum
, local maximum
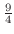 at
at
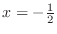 .
.
3.