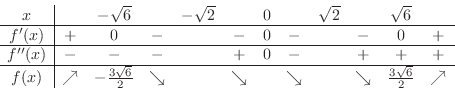Next: Polar Coordinates Up: Extreme Value of Functions Previous: Extreme Value of Functions Contents Index
 -axis
-axis
Asymptote Asymptote is a line for which a graph of function is getting close. Thus we have two cases. One is a line for which the denominator of a function is 0. The other one is that 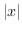 approaches infinity.
approaches infinity.
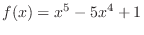 .
. | 1. |
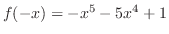 implies no symmetry. implies no symmetry. |
| 2. |
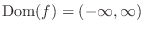 |
| 3. |
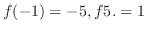 implies this function cross implies this function cross  -axis at least once -axis at least once |
| 4. |
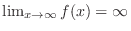 , ,
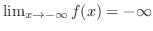 |
| 5. | By example2.22 |
 |

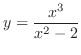 .
.
SOLUTION
| 1. |
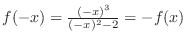 implies that implies that 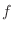 is symmetric is symmetric |
| with respect to the origin. | |
| 2. |
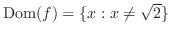 . . |
| 3. | To find an intersection with  -axis, set -axis, set 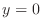 . . |
Then we have 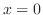 . . |
|
| 4. | When the denominator is 0, we have
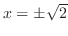 |
| as asymptotes. Next we can express the function as | |
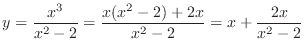 |
|
Thus 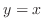 is asymptote. is asymptote. |
By quotient rule for differentiation,
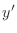 |
 |
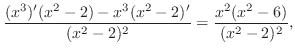 |
|
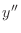 |
 |
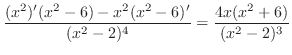 |
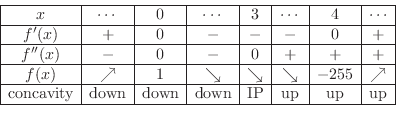
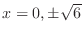 are the candidates for a critical point. Now write a concavity table, we have
are the candidates for a critical point. Now write a concavity table, we have