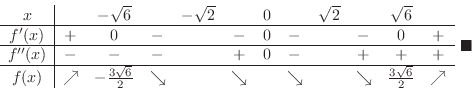Next: Curve Sketching Up: Differentiation Previous: Taylor's Theorem Contents Index
 in the neighborhood of
in the neighborhood of 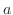 ,
,
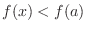 . Then we say
. Then we say  takes local maximum at
takes local maximum at  . if
. if
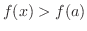 , then we say
, then we say  takes local minimum at
takes local minimum at  . local maximum and local minimum together called local extrema.
. local maximum and local minimum together called local extrema.
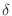 Neighborhood A
Neighborhood A 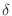 neghborhood of
neghborhood of 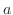 is a set of real number
is a set of real number  such that
such that
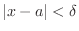 . In other words,
. In other words,
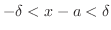 .
.
First Derivative Test
 is differentiable at
is differentiable at  . If
. If  takes local extrema at
takes local extrema at  , then
, then
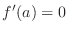 .
.
NOTE
If
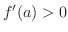 , then
, then  is increasing at
is increasing at  . If
. If
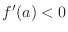 , then
, then  is decreasing at
is decreasing at  . In these cases,
. In these cases,  does not take local extrema. Thus we must have
does not take local extrema. Thus we must have
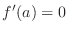 .
.
| Understanding |
|---|
Note that if a differentiable function 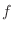 takes local extrema at takes local extrema at  . Then the slope of tangent line of . Then the slope of tangent line of 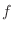 at at  is 0. is 0.
|
On the other hand, consider
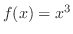 . Since
. Since
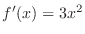 , the slope of the tangent line of
, the slope of the tangent line of  is 0 at
is 0 at 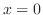 . But
. But  does not take local extrema at
does not take local extrema at 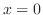 .
.
A function may take local extrema without being differentiable. Consider
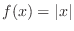 .
.
Criterion for Local Extrema
 is continuous on a neighborhood of
is continuous on a neighborhood of  . If
. If 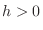 is small enough, then
is small enough, then
| 1. | If
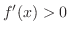 on on 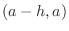 and and
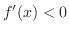 on on 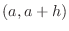 , , |
then  takes local maximum at takes local maximum at  . . |
|
|
|
|
| 2. | If
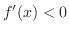 on on 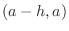 and and
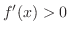 on on 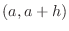 , , |
then  takes local minimum at takes local minimum at  . . |
|
|
|
|
| 3. | If
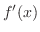 does not change the sign on does not change the sign on
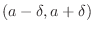 , , |
then 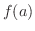 is not local extrema. is not local extrema. |
NOTE
1.  is strictly increasing function on
is strictly increasing function on ![$[a-h,a]$](img2104.png) and strictly decreasin on
and strictly decreasin on ![$[a,a+h]$](img2105.png) . Thus
. Thus  takes the local maximum at
takes the local maximum at  .
Inflection Point
an inflection point, point of inflection, flex, or inflection (inflexion) is a point on a curve at which the curvature or concavity changes sign from plus to minus or from minus to plus..
.
Inflection Point
an inflection point, point of inflection, flex, or inflection (inflexion) is a point on a curve at which the curvature or concavity changes sign from plus to minus or from minus to plus..
2nd Derivative Test
 is twice differentialbe on a interval containing
is twice differentialbe on a interval containing  and satisfies
and satisfies
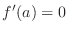 .
.
If
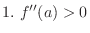 , then the graph of
, then the graph of 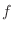 is concave up, and
is concave up, and 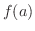 is local minimum
is local minimum
If
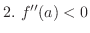 , then the graph of
, then the graph of 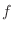 is concave down, and
is concave down, and 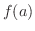 is local maximum
is local maximum
If
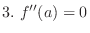 and concavity changes, then
and concavity changes, then 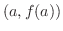 is an inflection point.
is an inflection point.
| Understanding |
|---|
Note that the 1st derivative represents the slope of the tangent line. Then the 2nd derivative represents how the slope of tangent line changes. If
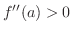 , then the slope of the tangent line is increasing in neighborhood of , then the slope of the tangent line is increasing in neighborhood of 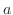 . .
|
NOTE Apply the above theorem to a function
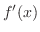 , Then
, Then
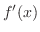 is increasing at
is increasing at  . Since
. Since
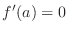 ,
,
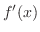 takes negative on
takes negative on
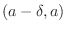 on positive on
on positive on
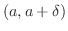 . Thus the graph of a function is concave up at
. Thus the graph of a function is concave up at  and takes a local minimum at
and takes a local minimum at  .
.
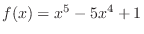 and concavity of the graph of
and concavity of the graph of  .
.| Extreme Point |
|---|
|
1. Find a domian of a fucntion
2. Find a critical point . 3. Find a candidate for inflection point. 4. Draw a concavity table |
SOLUTION
Since  is differentiable on
is differentiable on
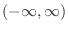 , if
, if  attains etremumat some point, then at the point
attains etremumat some point, then at the point
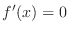 . Thus, we find
. Thus, we find  so that
so that
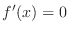 . Since
. Since
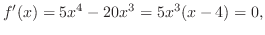
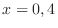 are the candidate for critical point. Next to check concavity of the graph of
are the candidate for critical point. Next to check concavity of the graph of 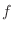 , we find
, we find
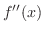 . Since
. Since
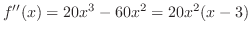
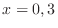 are the candidate for inflection point.
Now we create a concavity table.
are the candidate for inflection point.
Now we create a concavity table.
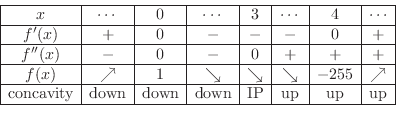
| Check |
|---|
How to find 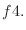 . Write . Write
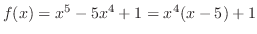 . Then substitute . Then substitute 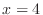 to get to get
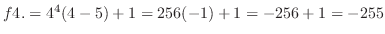 . .
|
By the 1st derivative test, 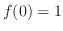 is a local maximum.
is a local maximum.
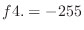 is a local minimum. By the 2nd derivative test,
is a local minimum. By the 2nd derivative test, 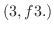 is an inflection point. The graph of function is concave down on the left-hand side of the inflection point and concave up on the right-hand side of the inflection point
is an inflection point. The graph of function is concave down on the left-hand side of the inflection point and concave up on the right-hand side of the inflection point

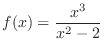 and concavity of the graph of
and concavity of the graph of  .
.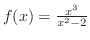 ,
,
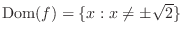 .
SOLUTION
By the quotient rule,
.
SOLUTION
By the quotient rule,
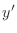 |
 |
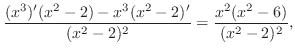 |
|
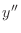 |
 |
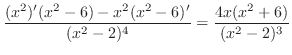 |
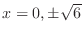 are candidates for a critical point. Now write a concavity table.
are candidates for a critical point. Now write a concavity table.