Next: Extreme Value of Functions Up: Differentiation Previous: Limit of Indeterminate Form Contents Index
Is it possible to express transcendental function  such as
such as 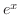 ,
, 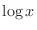 ,
, 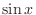 ,
,
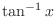 using polynomials? The next theorem answers such a question. transcendental function Let
using polynomials? The next theorem answers such a question. transcendental function Let
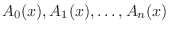 be polynomials in
be polynomials in  . Then a function
. Then a function 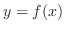 satisfies a polynomial equation
satisfies a polynomial equation
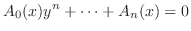
Taylor's Theorem
 is class
is class  on
on ![$[a,b]$](img1050.png) . Then there exists
. Then there exists 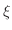 in
in 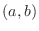 such that
such that
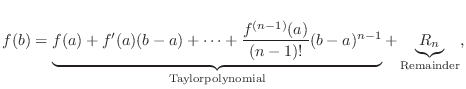
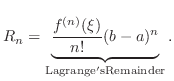
NOTE Note that for 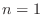 , we have
, we have
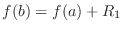 , where
, where
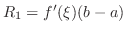 . Thus for
. Thus for 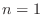 , Taylor's theorem is the same as Mean Value Theorem. For
, Taylor's theorem is the same as Mean Value Theorem. For 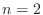 , we have
, we have
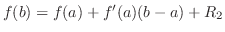 , where
, where 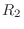 is the difference of the value of line
is the difference of the value of line
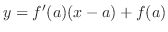 and function
and function  at
at 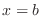 . In other words,
. In other words, 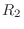 is an error caused by approximation of the value of
is an error caused by approximation of the value of 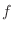 by the line. Similarly,
by the line. Similarly, 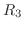 is an approximation error of
is an approximation error of 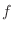 by a quadratic polynomial.
by a quadratic polynomial.
Proof
Let 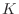 be an expression satisfying
be an expression satisfying
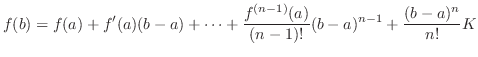
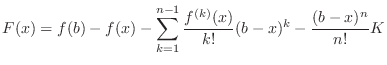
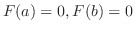 . Thus
. Thus 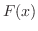 satisfies the condition of Rolle's Theorem . Thus
satisfies the condition of Rolle's Theorem . Thus
| Check |
|---|
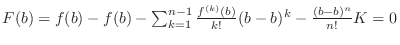 . .
|
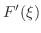 |
 |
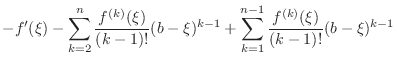 |
|
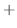 |
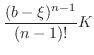 |
||
 |
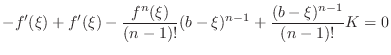 |
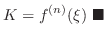
In Taylor's theorem with 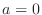 is called Maclaurin's Theorem. Set
is called Maclaurin's Theorem. Set 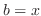 . Then we have
. Then we have
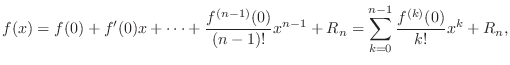
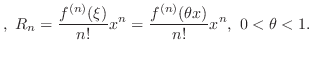
 , where
, where
![$\displaystyle \vert R_{n}\vert = \vert\frac{f^{(n)}(\theta x)}{n!}x^{n}\vert \l...
...ax_{\theta \in [0,1]}\vert f^{(n)}(\theta x)\vert)\frac{\vert x\vert^{n}}{n!}. $](img1951.png)
Understanding 1. Taylor polynomial around 
P(x) =
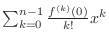 .
.
2. Lagrange's remainder
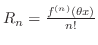
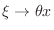 Note that
Note that
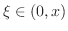 . Now we show
. Now we show
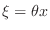 , where
, where
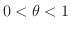 . Note that
. Note that
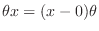 can represents all numbers form 0 to
can represents all numbers form 0 to 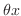 . Since
. Since
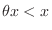 , we have
, we have
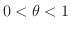 .
.
Error Estimate Error estimate is to find the bound for the absolute value of remainder term.
 .
.
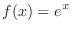
SOLUTION
Since
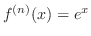 , we have
, we have
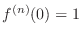 . Find a Taylor polynomial around
. Find a Taylor polynomial around 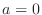 , we have
, we have
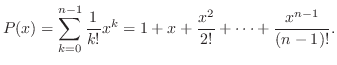
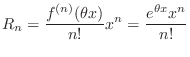
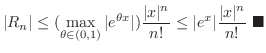
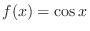
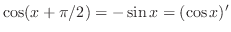
SOLUTION
Since
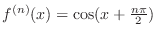 , we have
, we have
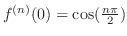 . Thus Taylor polynomial around
. Thus Taylor polynomial around 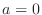 is
is
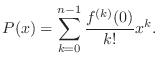 Now we divide this into two cases.
Now we divide this into two cases.
case 1. 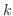 is even. Let
is even. Let 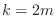 . Then
. Then
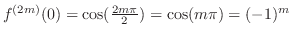
case 2. 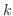 is odd. Let
is odd. Let 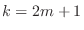 . Then
. Then
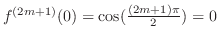 .
Thus
.
Thus
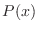 |
 |
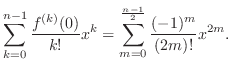 |
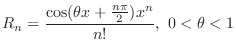
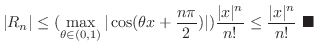
 is infinitely many times differentiable function on an interval containing
is infinitely many times differentiable function on an interval containing  . The by MacLaurin's theorem, we have
. The by MacLaurin's theorem, we have
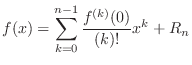
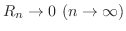 , then we can express
, then we can express  as
as
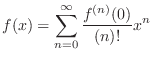
 .
.
MacLaurin Series Expansion of Basic Functions
| 1. |
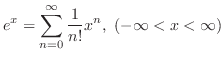 |
| 2. |
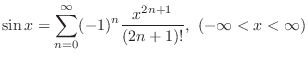 |
| 3. |
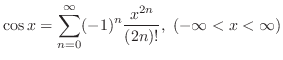 |
| 4. |
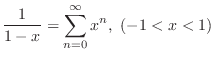 |
| 5. |
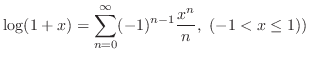 |
| 6. |
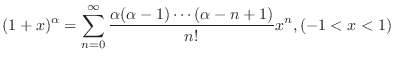 |
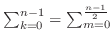 |
|---|
Note that 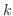 takes values from takes values from 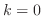 to to 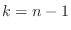 . Suppose . Suppose 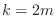 . Then for . Then for
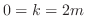 implies implies 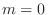 and for and for
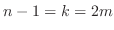 implies implies
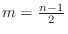 . .
|
Understanding In MacLaurin's theorem, a function is expressed by Taylor polynomial and error term. If the size of error estimate is getting close to 0, then we should be able to write  as infinite series.
as infinite series.
NOTE
| Check |
|---|
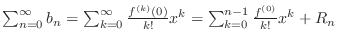 . .
|
To show MacLaurin series expansion, we need to show
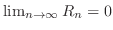 . But it is not easy to show
. But it is not easy to show
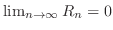 by using Lagrange's Remainder
by using Lagrange's Remainder 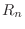 . So, we use different method. Suppose we express a MacLaurin series expansion of
. So, we use different method. Suppose we express a MacLaurin series expansion of  as
as
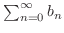 . Then showing
. Then showing 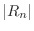 approachs 0 is the same as showing
approachs 0 is the same as showing
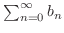 converges. To show
converges. To show
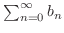 converges, it is useful Limit Ration Test.
Limit Ration Test
converges, it is useful Limit Ration Test.
Limit Ration Test
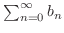 be a nonnegative series. If
be a nonnegative series. If
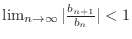 , then
, then
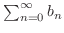 converges.
converges.
Radius of Convergence Replace 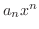 by
by 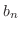 . Then
. Then
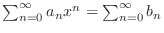 . Now
. Now
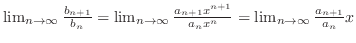 . Thus
. Thus
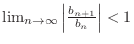 implies
implies
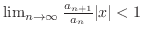 and for
and for
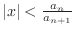 ,
,
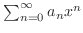 converges.
converges.
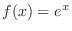 2.
2.
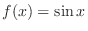
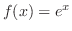 . Then since
. Then since
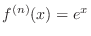 , we have
, we have
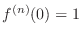 . Thus Taylor polynomial
. Thus Taylor polynomial 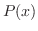 for
for 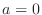 is
is
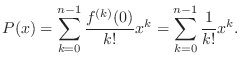
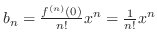 . Then apply the limit ration test.
. Then apply the limit ration test.
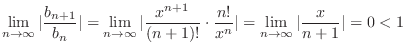
 ,
,
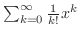 converges. Therefore
converges. Therefore
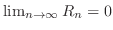 and,
and,
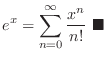
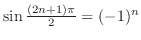 |
|---|
 .
.
2. Let
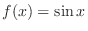 . Then since
. Then since
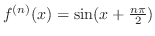 , we have
, we have
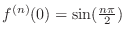 . Now for
. Now for 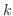 is even,
is even,
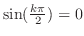 and for
and for 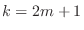 , we have
, we have
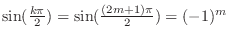 . Thus
. Thus
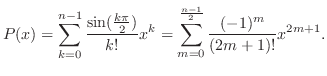
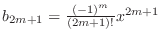 . Then by the limit ration test,
. Then by the limit ration test,
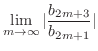 |
 |
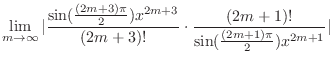 |
|
 |
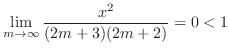 |
 ,
,
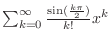 converges. Therefore,
converges. Therefore,
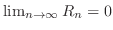 and
and
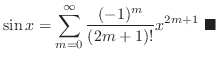
| Check |
|---|
Limit Ratio Test handles consecutive term. But for
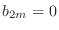 , we need to consider , we need to consider
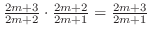 . .
|
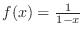 2.
2.
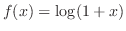
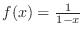 . Then since
. Then since
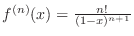 , we have
, we have
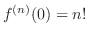 . Thus Taylor polynomial
. Thus Taylor polynomial 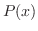 is
is
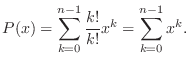 Let
Let
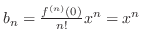 . Then by Limit Ratio Test, we have
. Then by Limit Ratio Test, we have
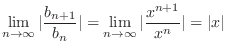
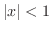 ,
,
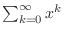 converges. Therefore,
converges. Therefore,
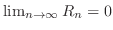 and
and
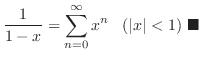
Radius of Convergence If
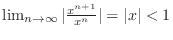 , then
, then
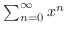 converges. Thus we say
converges. Thus we say 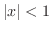 a radius of convergence.
a radius of convergence.
2. Let
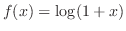 . Then
. Then
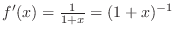 . Put
. Put 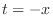 . Then
. Then
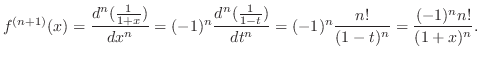
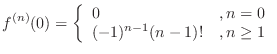
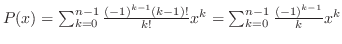 .
Let
.
Let
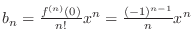 and apply Limit Ratio Test. Then
and apply Limit Ratio Test. Then
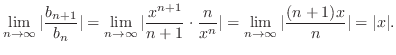
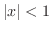 ,
,
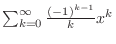 converges. Therefore,
converges. Therefore,
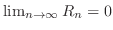 and
and
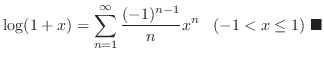
Landau little o
 has Maclaurin series expansion. Then
has Maclaurin series expansion. Then
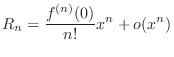
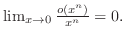
Proof
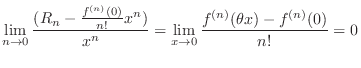
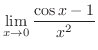
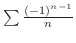 |
|---|
Show
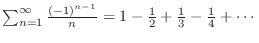 converges. converges.
|
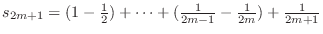
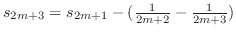
Thus
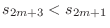 . Then a sequence
. Then a sequence 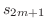 is decreasing and bouded blow by 0. Thus,
is decreasing and bouded blow by 0. Thus,
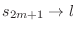 . On the other hand, since
. On the other hand, since
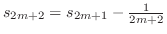 ,
,
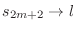 . Therefore,
. Therefore,
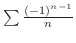 converges.
converges.
SOLUTION
Since the denominator is 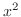 , we find Taylor polynomial of 2nd degree of
, we find Taylor polynomial of 2nd degree of
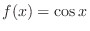 .
.
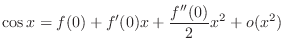
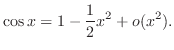
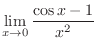 |
 |
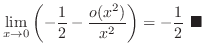 |
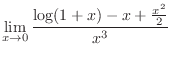
SOLUTION Since the denominator is 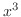 , we find Taylor polynomial of 3rd degree of
, we find Taylor polynomial of 3rd degree of
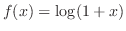 .
.
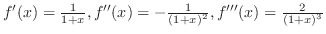 implies ,
implies ,
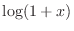 |
 |
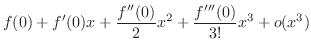 |
|
 |
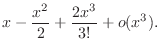 |
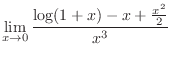 |
 |
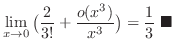 |
(c)
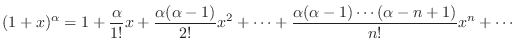
??????
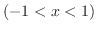
(d)
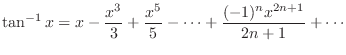 ,
,
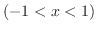
(a) By the exercise 1(d)we can obtain
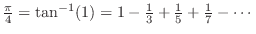 Now using this fact, calculate
Now using this fact, calculate 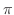
(b)
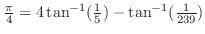 is called Machin's formulaUsing this formula, calculate
is called Machin's formulaUsing this formula, calculate 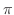 100 digts after the decimal point
100 digts after the decimal point