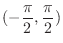Next: Limit of Indeterminate Form Up: Differentiation Previous: Higher Order Derivatives Contents Index
As a property of continuous function, we have Intermediate Value Theorem and Extreme Value Theorem. Then we ask what kind of properties differentiable functions have.
Mean Value Theorem
 be continuous on
be continuous on ![$[a,b]$](img1050.png) and differentiable on
and differentiable on 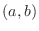 . Then there exists at least one
. Then there exists at least one
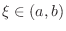 satisfying
satisfying
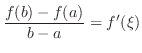
Understanding The Mean Value Theorem says that if you drive 60km in 1hr, then your average speed is 60km/hr and you must drive your car faster than 60km/hr at least once.
NOTE Note that
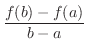 can be thought of the slope of line passing through two points
can be thought of the slope of line passing through two points
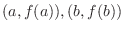 . Then
. Then
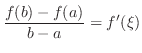 for
for
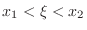 can be thought of existence of tangent line with the slope is the same. Suppose that
can be thought of existence of tangent line with the slope is the same. Suppose that  is the position of a car and the interval
is the position of a car and the interval ![$[a,b]$](img1050.png) represents time. Then,
represents time. Then,
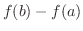 represents the distance moved during
represents the distance moved during 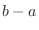 . In other words,
. In other words,
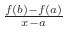 represents the average speed.
represents the average speed.
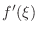 represents the instantaneous speed.
represents the instantaneous speed.
Rolle's Theorem
 be continuous on
be continuous on ![$[a,b]$](img1050.png) and differentiable on
and differentiable on 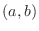 . If
. If
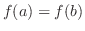 , then there is at least one number
, then there is at least one number 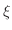 in
in 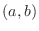 such that
such that
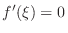
Understanding If you shoot a ball upward and if the ball comes back to you, then there is a moment the ball stopped in the air.
Proof
Since this function is continuous on ![$[a,b]$](img1050.png) , by Extreme Value Theorem,
, by Extreme Value Theorem,  attains the maimum value and the minimum value in the interval
attains the maimum value and the minimum value in the interval ![$[a,b]$](img1050.png) . Let
. Let 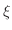 be such that
be such that 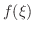 is maximum. Then we have
is maximum. Then we have
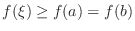 . Thus
. Thus
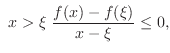
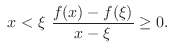
One Side
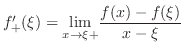
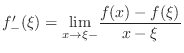
Since  is differentiable, the left-hand side of the above inequalities is
is differentiable, the left-hand side of the above inequalities is
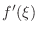 and we have.
and we have.
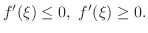
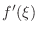 exists. Thus
exists. Thus
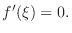
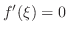

![$f(x) = x^3 - x^2 , [-1,1]$](img1739.png)
SOLUTION
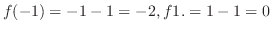 and
and
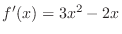 . Then
. Then
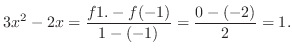
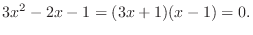
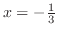 ,
, 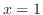 . But
. But 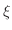 must be in
must be in 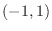 . Therefore,
. Therefore,
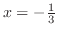 is the admissible value
is the admissible value

![$f(x) = \sin^{-1}{x} , [0,1]$](img1747.png)
SOLUTION Note that
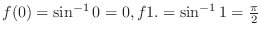 and
and
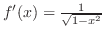 . Then we find
. Then we find  satisfying
satisfying
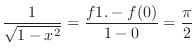
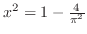 implies
implies
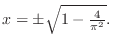 We note that
We note that
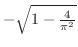 is not in
is not in 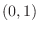
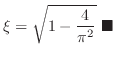
To find  satisfying
satisfying
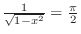 , we squared both sides of the equation. Then
, we squared both sides of the equation. Then
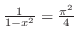 . Now take the reciprocal. Then
. Now take the reciprocal. Then
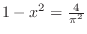 which implies
which implies
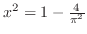 .
.
| Idea |
|---|
Connect two points  and and  by straight line and think of this line as by straight line and think of this line as  -axis. Then the function takes 0 at -axis. Then the function takes 0 at 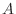 and and 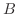 and we can use Rolle's Theorem. and we can use Rolle's Theorem.
|
Proof of Mean Value Theorem assuming Rolle's Theorem
The idea here is to create the function which satisfies the conditions of Rolle's theorem. The equation 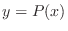 of line passing through two points
of line passing through two points 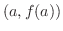 ,
,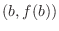 is given by
is given by
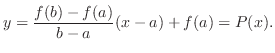
 be the
be the
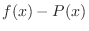 . Then
. Then
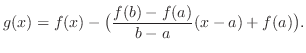
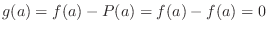 and
and
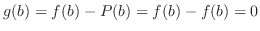 which satisfy the condition of Rolle's Theorem. Thus by Rolle's Theorem, there exists at least one
which satisfy the condition of Rolle's Theorem. Thus by Rolle's Theorem, there exists at least one
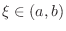 such that
such that
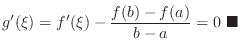
Increasing/Decreasing The graph of a function  is said to be increasing .
is said to be increasing .
Increasing/Decreasing Functions
If  is defined in the neighborhood of
is defined in the neighborhood of  and for
and for 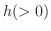 ,
,  satisfies
satisfies
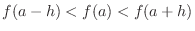 . Then
. Then  is increasing at
is increasing at 
If  is defined in the neighborhood of
is defined in the neighborhood of  and for
and for 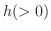 ,
,  satisfies
satisfies
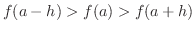 . Then
. Then  is decreasing at
is decreasing at 
The neighborhood of  is the interval
is the interval
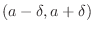 .
.
Increasing/Decreasing Functions
 be differentiable function at
be differentiable function at  . If
. If
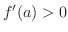 , then
, then  is increasing at
is increasing at  . If
. If
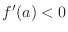 , then
, then  is decreasing at
is decreasing at  .
. Understanding Consider the curve and a point whose slope of tangent line is positive. Then the neighborhood of this point, the curve is concave up
NOTE
Consider
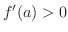 .
.
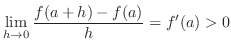
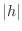 is small enough, then
is small enough, then
| Check |
|---|
For 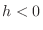 , let , let 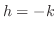 . Then . Then 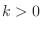 and and
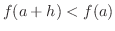 becomes becomes
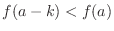 . .
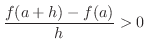
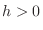 implies implies
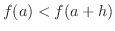 and and 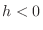 implies implies
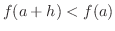 . Therefore, . Therefore,  is increasing at is increasing at  . .
|
Application of Mean Value Theorem
Properties of Differentiable Functions
 be continuous on
be continuous on ![$[a,b]$](img1050.png) and differentiable on
and differentiable on 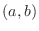 . Then
. Then
1. If
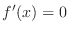 for all
for all  in
in 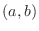 , then
, then  is constant function on
is constant function on ![$[a,b]$](img1050.png) .
.
2. If
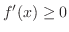 for all
for all
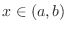 and there are only finite number of
and there are only finite number of  satisfying
satisfying
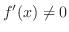 , then
, then  is strictly increasing on
is strictly increasing on ![$[a,b]$](img1050.png) .
.
Understanding The slope of tangent line becomes 0 only at finite point.
NOTE
we need to show for any 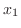 and
and 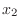 satisfying
satisfying
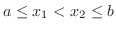 ,
,
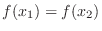 .
Given a closed interval
.
Given a closed interval ![$[a,b]$](img1050.png) , we choose
, we choose 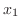 and
and 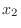 so that
so that
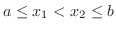 . Then since
. Then since 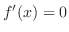 for all
for all  , for any
, for any 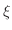 satisfying
satisfying
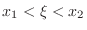 , we have
, we have
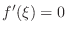 . Thus
. Thus
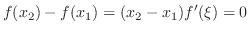
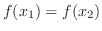 .
.
If
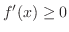 , then
, then
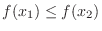 . If
. If
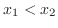 and
and
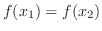 , then by 1),
, then by 1),  is constant on
is constant on
![$[x_{1},x_{2}]$](img1798.png) and
and
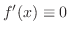 which violates the condition. Thus,
which violates the condition. Thus,
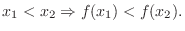
 is strictly increasing function on
is strictly increasing function on ![$[a,b]$](img1050.png) .
.
Same Derivatives
 and
and  be continuous on
be continuous on ![$[a,b]$](img1050.png) and differentiable on
and differentiable on  . If
. If
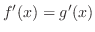 on
on 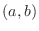 , then
, then
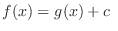 where c is constant
where c is constant
Proof
Let
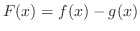 . Then
. Then
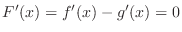 implies
implies 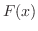 is constant. Thus
is constant. Thus
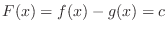

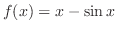 is strictly increasing on
is strictly increasing on
![$\displaystyle{[-\frac{\pi}{2},\frac{\pi}{2}]}$](img498.png)
Need to show 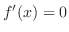 is satisfied by a finite number of
is satisfied by a finite number of  .
.
SOLUTION
Note that since
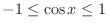 , we have
, we have
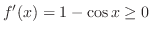 . Now
. Now
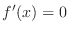 implies that
implies that
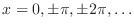 . Then
. Then 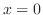 is the only one which is in
is the only one which is in
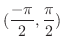 . Thus
. Thus  is strictly increasing function on
is strictly increasing function on
![$\displaystyle{[-\frac{\pi}{2},\frac{\pi}{2}]}$](img498.png)

To compare, we can use strictly increasing.
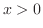 , show the following inequality is true .
, show the following inequality is true .
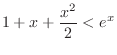
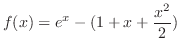 . To show
. To show 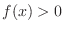 If we can show
If we can show
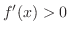 , then
, then  is strictly increasing. So if
is strictly increasing. So if 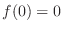 , then for
, then for 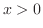 ,
, 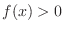 .
Then since
.
Then since 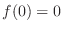 , if we can show
, if we can show 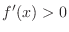 , then we can show
, then we can show 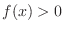 . So we find
. So we find
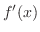 . Since
. Since
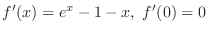
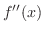 . Then
. Then
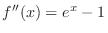
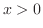 , we have
, we have 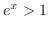 . Thus
. Thus
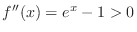 which implies that
which implies that
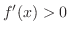 . Therefore
. Therefore 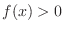

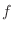 increases and the intervals on which
increases and the intervals on which 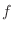 decreases.
decreases.
(a) Find the greatest possible value for 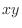 given that
given that  and
and  are both positive and
are both positive and 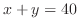
(b) Find the largest possible area for a rectangle with base on the  -axis and upper vertices on the curve
-axis and upper vertices on the curve
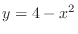
(c) Find the largest possible area for a rectangle inscibed in a circle of radius 4
(d) Find the shortest distance between the ellipse
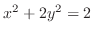 and a the line
and a the line 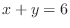
![[*]](crossref.png) enshu:2-4-2
enshu:2-4-2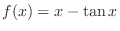 is an strictly increasing function on the interval
is an strictly increasing function on the interval